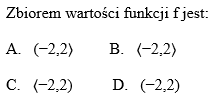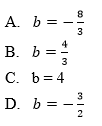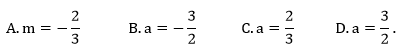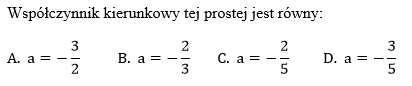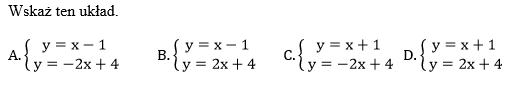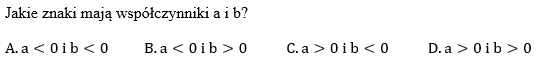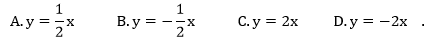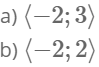Zadania maturalne z Matematyki

Tematyka: funkcje liniowe.

Zadania pochodzą z oficjalnych arkuszy maturalnych CKE, które służyły przeprowadzaniu majowych egzaminów. Czteroznakowy kod zapisany przy każdym zadaniu wskazuje na jego pochodzenie: S/N – „stara”/”nowa” formuła; P/R – poziom podstawowy/rozszerzony; np. 08 – rok 2008.

Zbiór zadań maturalnych w formie arkuszy, możesz pobrać >> TUTAJ <<.

Zadanie 1. (NP15)
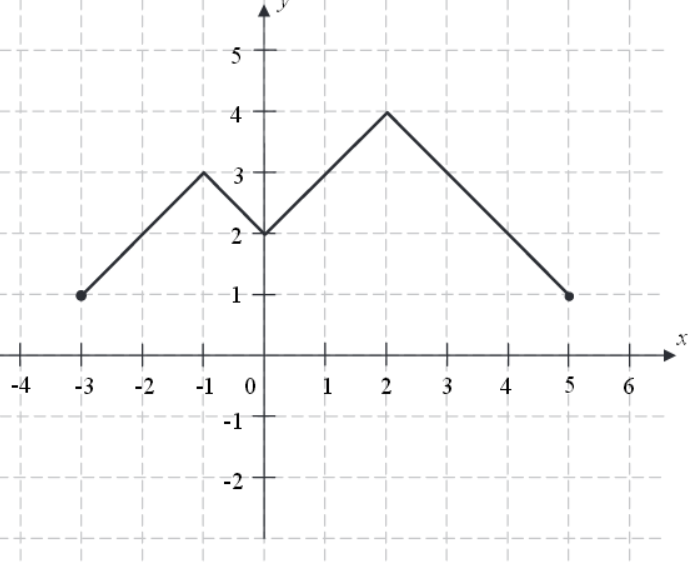
Na rysunku przedstawiono wykres funkcji f.

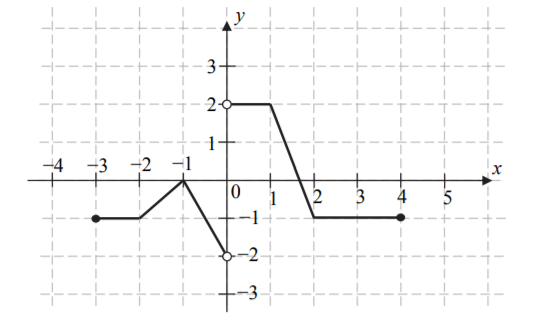
Zadanie 2. (NP15)
Na wykresie funkcji liniowej określonej wzorem f(x)=(m−1)x+3 leży punkt S=(5,−2). Zatem:

Zadanie 3. (NP15)
Funkcja liniowa f określona wzorem f(x) = 2x + b ma takie samo miejsce zerowe, jakie ma funkcja g(x) = −3x + 4. Stąd wynika, że:

Zadanie 4. (NP15)
Prosta  l o równaniu y=m2x+3 jest równoległa do prostej k o równaniu y=(4m−4)x−3. Zatem:

Zadanie 5. (NP15)
Proste o równaniach: y=2mx−m2−1 oraz y=4m2x+m2+1 są prostopadłe dla:

Zadanie 6. (NP16)
Proste o równaniach 2x−3y=4 i 5x−6y=7 przecinają się w punkcie P. Stąd wynika, że:

Zadanie 7. (NP16)
Dana jest funkcja liniowa f(x) =x + 6. Miejscem zerowym tej funkcji jest liczba:

Zadanie 8. (NP16)
Proste opisane równaniami y= oraz y=mx+ są prostopadłe, gdy:

Zadanie 9. (NP17)
Miejscem zerowym funkcji liniowej f(x)= (x+1)−12 jest liczba:

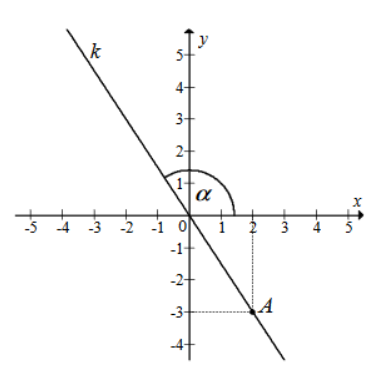
Zadanie 10. (NP17)
Na rysunku przedstawiona jest prosta k o równaniu y=ax, przechodząca przez punkt A=(2,−3) i przez początek układu współrzędnych, oraz zaznaczony jest kąt α nachylenia tej prostej od osi Ox.

Zadanie 11. (NP17)
Na płaszczyźnie z układem współrzędnych proste k i l przecinają się pod kątem prostym w punkcie A=(−2,4). Prosta k jest określona równaniem
y=−x+.  Zatem prostą l opisuje równanie.

Zadanie 13. (NP18)
Liczba 1 jest miejscem zerowym funkcji liniowej f(x)=ax+b, a punkt M=(3,−2) należy do wykresu tej funkcji. Współczynnik a we wzorze tej funkcji jest równy:

Zadanie 14. (NP18)
Proste   o równaniach y=(m+2)x+3  oraz y=(2m−1)x−3 są równoległe, gdy:

Zadanie 15. (SP15)
Miejscem zerowym funkcji liniowej określonej wzorem f(x)- +4 jest:

Zadanie 16. (SP15)
Punkt M=( ,3) należy do wykresu funkcji liniowej określonej wzorem f(x)=(3−2a)x+2. Wtedy:

Zadanie 17. (SP15)
Na rysunku przedstawiono fragment prostej o równaniu y=ax+b.

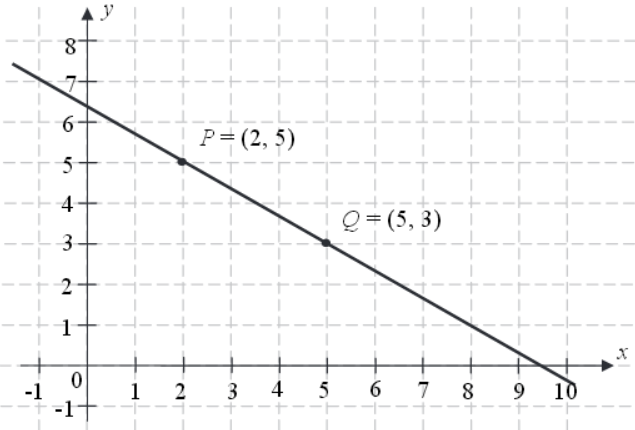
Zadanie 18. (SP15)
Na rysunku przedstawiono wykres funkcji f.

Funkcja h określona jest dla x∈⟨−3,5⟩ wzorem h(x)=f(x)+q, gdzie q jest pewną liczbą rzeczywistą. Wiemy, że jednym z miejsc zerowych funkcji h jest liczba x0=−1.

a) Wyznacz q.
b) Podaj wszystkie pozostałe miejsca zerowe funkcji h.

Zadanie 19. (SP14)
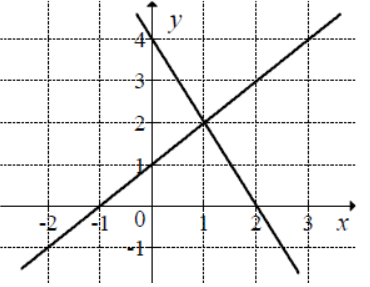
Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań.

Zadanie 20. (SP14)
Funkcja liniowa f(x)=(m2−4)x+2 jest malejąca, gdy:

Zadanie 21. (SP14)
Punkt C=(0,2) jest wierzchołkiem trapezu ABCD, którego podstawa AB jest zawarta w prostej o równaniu y=2x−4. Wskaż równanie prostej zawierającej podstawę CD.

Zadanie 22. (SP14)
O funkcji liniowej f wiadomo, że f(1)=2. Do wykresu tej funkcji należy punkt P=(−2,3). Wzór funkcji f to:

Zadanie 23. (SP13)
Rozwiązaniem układu równań     jest para liczb:

Zadanie 24. (SP13)
Punkt A=(0,1) leży na wykresie funkcji liniowej f(x)=(m−2)x+m−3. Stąd wynika, że:

Zadanie 25. (SP13)
Prosta o równaniu y= x+1 jest prostopadła do prostej o równaniu y=− x−1. Stąd wynika, że:

Zadanie 26. (SP13)
Na rysunku przedstawiony jest fragment wykresu pewnej funkcji liniowej y=ax+b.

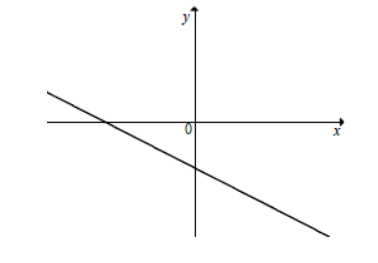
Zadanie 27. (SP13)
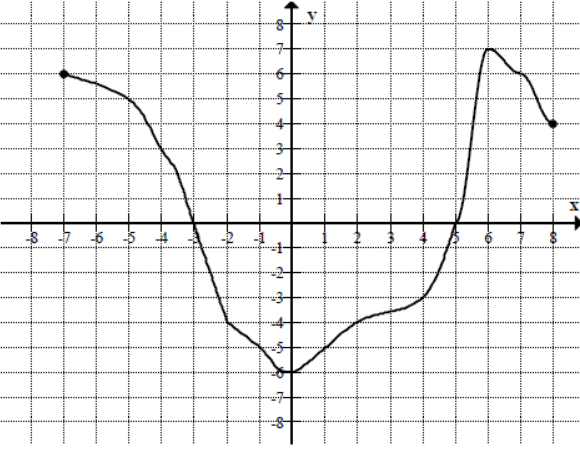
Na rysunku przedstawiony jest wykres funkcji f(x) określonej dla x∈[−7,8].

Zadanie 28. (SP12)
Funkcja liniowa f jest określona wzorem f(x)=ax+6, gdzie a>0. Wówczas spełniony jest warunek:

Zadanie 29. (SP12)
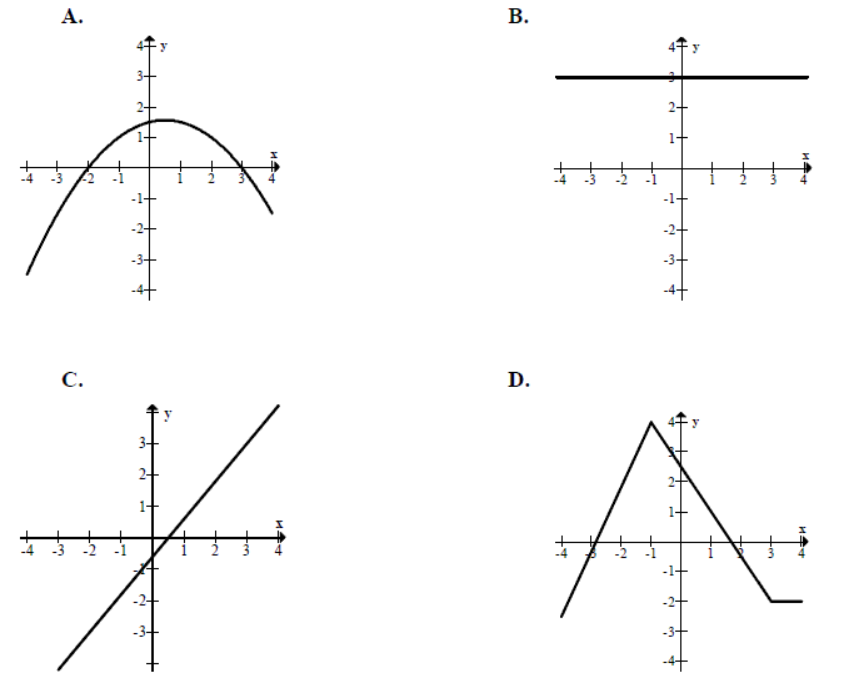
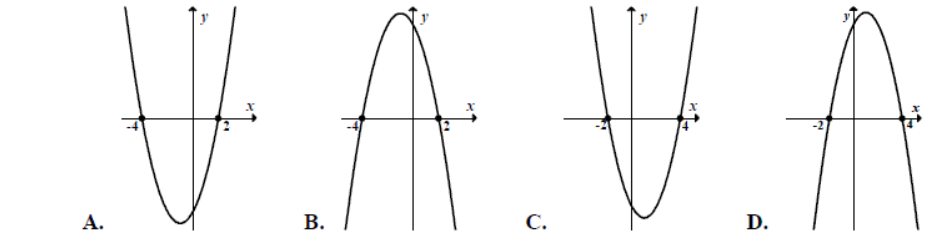
Wskaż wykres funkcji, która w przedziale ⟨−4,4⟩ ma dokładnie jedno miejsce zerowe.

Zadanie 30. (SP12)
Wskaż równanie prostej równoległej do prostej o równaniu 3x−6y+7=0

Zadanie 31. (SP11)
Układ równań ma nieskończoność rozwiązań jeśli:

Zadanie 32. (SP11)
Dane są funkcje liniowe f(x)=x−2 oraz g(x)=x+4 określone dla wszystkich liczb rzeczywistych x. Wskaż, który z poniższych wykresów jest wykresem funkcji h(x)=f(x)⋅g(x):

Zadanie 33. (SP11)
Funkcja liniowa określona jest wzorem f(x)=− x +4. Miejscem zerowym tej funkcji jest liczba:

Zadanie 34. (SP11)
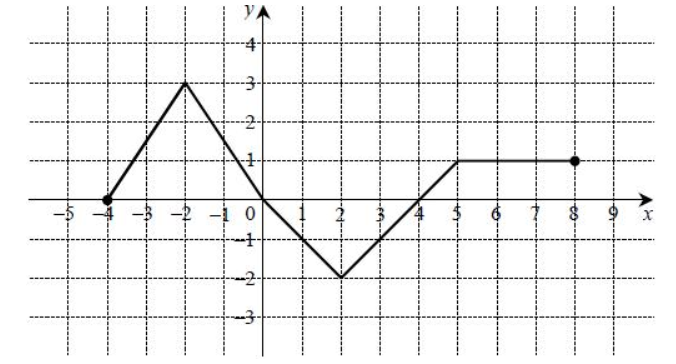
Na rysunku przedstawiono wykres funkcji f.

Odczytaj z wykresu i zapisz:
a) Zbiór wartości funkcji f.
b) Przedział maksymalnej długości, w którym f jest malejąca.

Zadanie 35. (SP10)
Prosta o równaniu y=−2x+(3m+3) przecina w układzie współrzędnych oś Oy w punkcie (0,2). Wtedy:

Zadanie 37. (SP10)
Współczynnik kierunkowy prostej równoległej do prostej o równaniu y=−3x+5 jest równy:

Zadanie 38. (SP09)
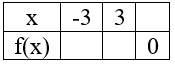
Funkcja f określona jest wzorem f(x)=

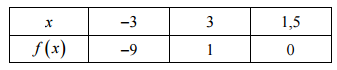
a) Uzupełnij tabelę:

b) Narysuj wykres funkcji f(x ) .
c) Podaj liczby całkowite x , spełniające nierówność f(x) ≥ − 6 .

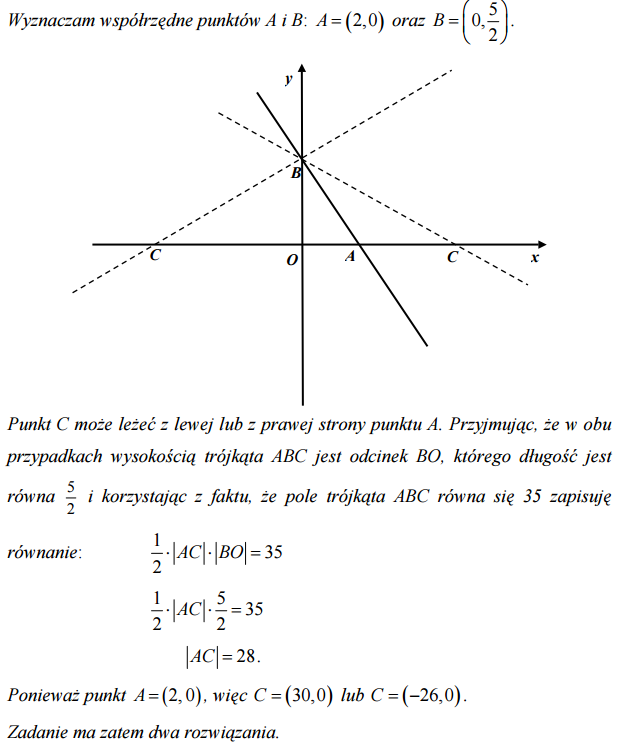
Zadanie 39. (SP08)
Prosta o równaniu 5x + 4y − 10 = 0  przecina oś Ox  układu współrzędnych w punkcie A  oraz oś Oy  w punkcie B . Oblicz współrzędne wszystkich punktów C  leżących na osi Ox  i takich, że trójkąt ABC  ma pole równe 35 .