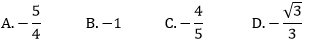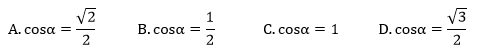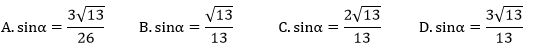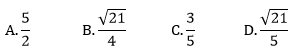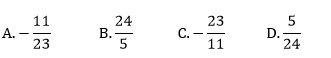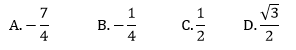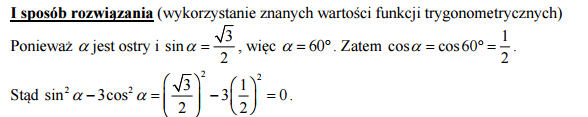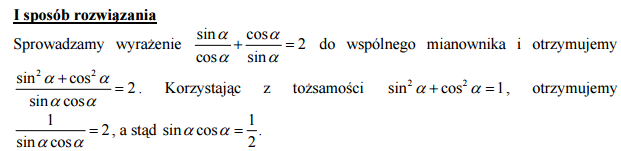Zadania maturalne z Matematyki

Tematyka: funkcje trygonometryczne.

Zadania pochodzą z oficjalnych arkuszy maturalnych CKE, które służyły przeprowadzaniu majowych egzaminów. Czteroznakowy kod zapisany przy każdym zadaniu wskazuje na jego pochodzenie: S/N – „stara”/”nowa” formuła; P/R – poziom podstawowy/rozszerzony; np. 08 – rok 2008.

Zbiór zadań maturalnych w formie arkuszy, możesz pobrać >> TUTAJ <<.

Zadanie 1. (NP15) 
W układzie współrzędnych zaznaczono punkt P=(−4,5). Tangens kąta α zaznaczonego na rysunku jest równy:

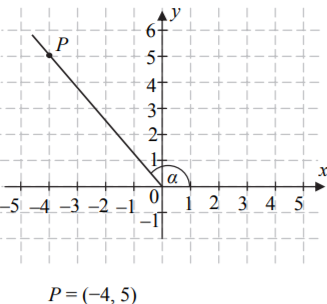
Zadanie 2. (NP15) 
Jeżeli oraz   , to:

 Zadanie 3. (NP15) 
Miara kąta wpisanego w okrąg jest o 30st  mniejsza od miary kąta środkowego opartego na tym samym łuku. Wynika stąd, że miara kąta wpisanego jest równa:

Zadanie 4. (NP16) 
Kąt α jest ostry i tgα= . Wtedy:

Zadanie 5. (NP17) 
Jeżeli m=sin50st  to:

Zadanie 6. (NP18) 
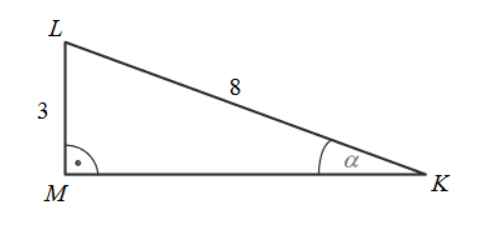
Przyprostokątna LM trójkąta prostokątnego KLM ma długość 3, a przeciwprostokątna KL ma długość 8 (zobacz rysunek).Wtedy miara α kąta ostrego LKM tego trójkąta spełnia warunek:

Zadanie 7. (SP15) 
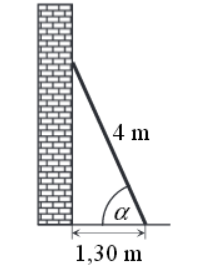
Drabinę o długości 4 metrów oparto o pionowy mur, a jej podstawę umieszczono w odległości 1,30 m od tego muru (zobacz rysunek).

 Zadanie 8. (SP15) 
Kąt α jest ostry i sinα=. Wówczas cosα jest równy:

Zadanie 9. (SP16) 
Kąt α jest ostry i .  Oblicz wartość wyrażenia sinα⋅cosα.

Zadanie 10. (SP14) 
Kąt α jest kątem ostrym i tgα= , to wartość wyrażenia  jest równa:

Zadanie 11. (SP14) 
Wysokość trapezu równoramiennego o kącie ostrym 60st i ramieniu długości jest równa:

 Zadanie 12. (SP14) 
Kąt środkowy oparty na łuku, którego długość jest równa   długości okręgu, ma miarę:

Zadanie 13. (SP13) 
Kąt α jest ostry i sinα=. Wartość wyrażenia cos²α−2 jest równa:

Zadanie 14. (SP13) 
Kąt α jest ostry i sinα=. Oblicz wartość wyrażenia sin²α−3cos²α.

 Zadanie 15. (SP12) 
Liczba   jest równa:

Zadanie 16. (SP12) 
W trójkącie prostokątnym ABC odcinek AB jest przeciwprostokątną i |AB|=13 oraz |BC|=12 . Wówczas sinus kąta ABC jest równy.

 Zadanie 17. (SP11) 
Kąt α jest ostry i cosα=. Wtedy:

Zadanie 18. (SP11) 
Wartość wyrażenia   jest równa:

Zadanie 19. (SP11)
Kąt α jest ostry i . Oblicz wartość wyrażenia cosα⋅sinα.

Zadanie 20. (SP10) 
Kąt α jest ostry i sinα=. Wartość wyrażenia 2−cos²α jest równa:

Zadanie 21. (SP10) 
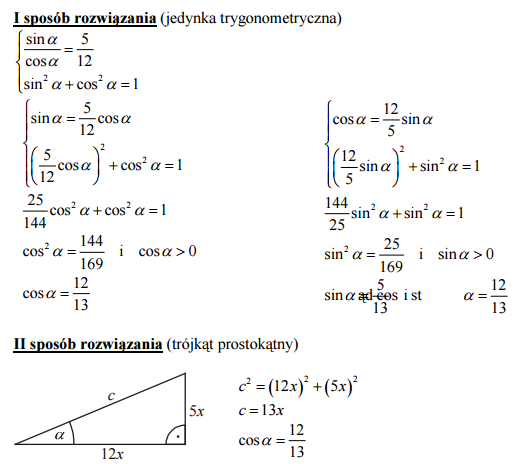
Kąt α jest ostry i tgα=. Oblicz cosα.

Zadanie 22. (SP09) 
Miara jednego z kątów ostrych w trójkącie prostokątnym jest równa α.

a) Uzasadnij, że spełniona jest nierówność sin α− tg α < 0.
b) Dla oblicz wartość wyrażenia cos³α +cosα ⋅sin ²α .

Zadanie 23. (SP07) 
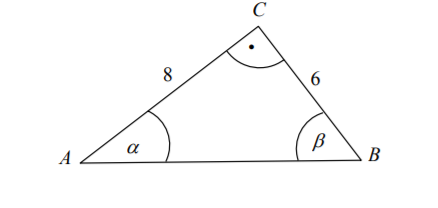
Korzystając z danych przedstawionych na rysunku, oblicz wartość wyrażenia:

Zadanie 24. (3 pkt)
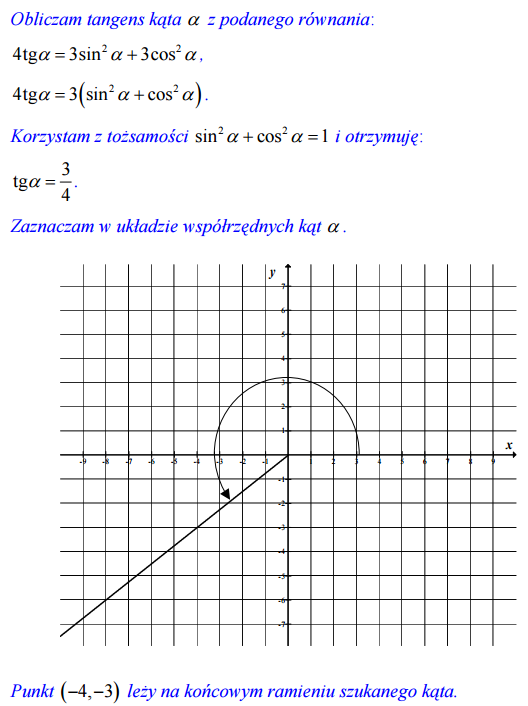
Wiedząc, że oraz

a) Oblicz tgα.
b) Zaznacz w układzie współrzędnych kąt i podaj współrzędne dowolnego punktu, różnego od początku układu współrzędnych, który leży na końcowym ramieniu tego kąta.