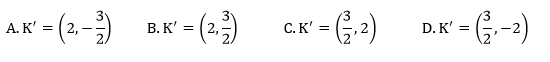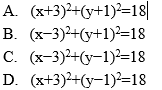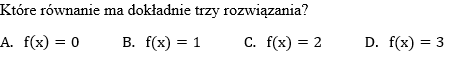Zadania maturalne z Matematyki
Tematyka: geometria analityczna.
Zadania pochodzą z oficjalnych arkuszy maturalnych CKE, które służyły przeprowadzaniu majowych egzaminów. Czteroznakowy kod zapisany przy każdym zadaniu wskazuje na jego pochodzenie: S/N – „stara”/”nowa” formuła; P/R – poziom podstawowy/rozszerzony; np. 08 – rok 2008.
Zbiór zadań maturalnych w formie arkuszy, możesz pobrać >> TUTAJ <<.
Zadanie 1. (NP15)
Dane są punkty M=(−2,1) i N=(−1,3). Punkt K jest środkiem odcinka MN. Obrazem punktu K w symetrii względem początku układu współrzędnych jest punkt:
Zadanie 2. (NP15)
W układzie współrzędnych dane są punkty A=(−43,−12), B=(50,19). Prosta AB przecina oś Ox w punkcie P. Oblicz pierwszą współrzędną punktu P.
Zadanie 3. (NP16)
W układzie współrzędnych dane są punkty A=(a,6) oraz B=(7,b). Środkiem odcinka AB jest punkt M=(3,4). Wynika stąd, że:
Zadanie 4. (NP17)
Dany jest okrąg o środku S=(2,3) i promieniu r=5. Który z podanych punktów leży na tym okręgu?
Zadanie 5. (NP17)
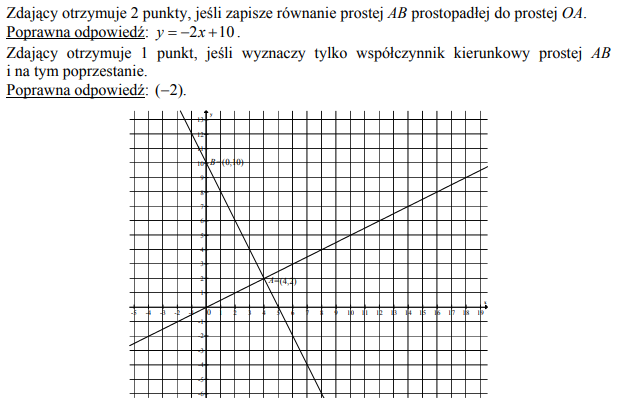
Dane są punkty A=(−4,0) i M=(2,9) oraz prosta k o równaniu y=−2x+10. Wierzchołek B trójkąta ABC to punkt przecięcia prostej k z osią Ox układu współrzędnych, a wierzchołek C jest punktem przecięcia prostej k z prostą AM. Oblicz pole trójkąta ABC.
Zadanie 6. (NP18)
Punkt K=(2,2) jest wierzchołkiem trójkąta równoramiennego KLM, w którym |KM|=|LM|. Odcinek MN jest wysokością trójkąta i N=(4,3). Zatem:
Zadanie 7. (NP18)
W układzie współrzędnych punkty A=(4,3) i B=(10,5) są wierzchołkami trójkąta ABC. Wierzchołek C leży na prostej o równaniu y=2x+3. Oblicz współrzędne punktu C, dla którego kąt ABC jest prosty.
Zadanie 8. (SP15)
Dane są punkty M=(3,−5) oraz N=(−1,7). Prosta przechodząca przez te punkty ma równanie:
Zadanie 9. (SP15)
Dane są punkty P=(−2,−2), Q=(3,3). Odległość punktu P od punktu Q jest równa:
Zadanie 10. (SP15)
Punkt K=(−4,4) jest końcem odcinka KL, punkt L leży na osi Ox, a środek S tego odcinka leży na osi Oy. Wynika stąd, że:
Zadanie 11. (SP15)
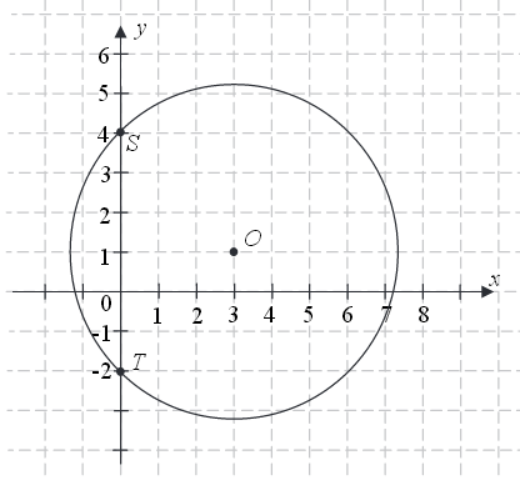
Okrąg przedstawiony na rysunku ma środek w punkcie O=(3,1) i przechodzi przez punkty S=(0,4) i T=(0,−2). Okrąg ten jest opisany przez równanie:
Zadanie 12. (SP14)
Liczba punktów wspólnych okręgu o równaniu (x+2)2+(y−3)2=4 z osiami układu współrzędnych jest równa:
Zadanie 13. (SP13)
Punkty A=(−1,2) i B=(5,−2) są dwoma sąsiednimi wierzchołkami rombu ABCD. Obwód tego rombu jest równy:
Zadanie 14. (SP13)
Punkt S=(−4,7) jest środkiem odcinka PQ, gdzie Q=(17,12). Zatem punkt P ma współrzędne:
Zadanie 15. (SP13)
Odległość między środkami okręgów o równaniach (x+1)2+(y−2)2=9 oraz x2+y2=10 jest równa:
Zadanie 16. (SP12)|
Punkt A ma współrzędne (5,2012). Punkt B jest symetryczny do punktu A względem osi Ox, a punkt C jest symetryczny do punktu B względem osi Oy . Punkt C ma współrzędne:
Zadanie 17. (SP12)|
Na okręgu o równaniu (x−2)2+(y+7)2=4 leży punkt:
Zadanie 18. (SP12)
Wyznacz równanie symetralnej odcinka o końcach A=(−2,2) i B=(2,10).
Zadanie 19. (SP11)
Prosta k ma równanie y=2x−3. Wskaż równanie prostej l równoległej do prostej k i przechodzącej przez punkt D o współrzędnych (−2,1).
Zadanie 20. (SP11)
Styczną do okręgu (x−1)2+y2−4=0 jest prosta równaniu:
Zadanie 21. (SP11)
Okrąg o środku w punkcie S=(3,7) jest styczny do prostej o równaniu y=2x−3. Oblicz współrzędne punktu styczności.
Zadanie 22. (SP10)
Wskaż równanie okręgu o promieniu 6.
Zadanie 23. (SP10)
Punkty A=(−5,2) i B=(3,−2) są wierzchołkami trójkąta równobocznego ABC. Obwód tego trójkąta jest równy:
Zadanie 24. (SP09)
Punkty B = (0,10) i O = (0,0) są wierzchołkami trójkąta prostokątnego OAB, w którym |∡OAB |=. Przyprostokątna OA zawiera się w prostej o równaniu y = x . Oblicz współrzędne punktu A i długość przyprostokątnej OA.
Zadanie 25. (SP08)
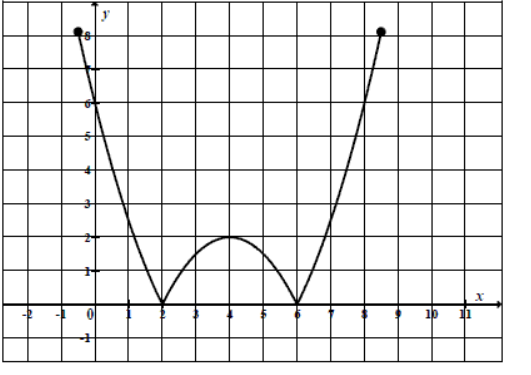
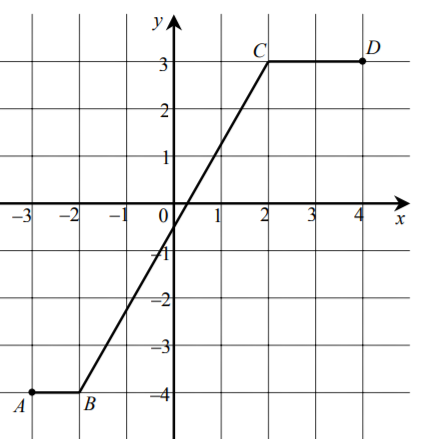
Na poniższym rysunku przedstawiono łamaną ABCD , która jest wykresem funkcji y = f(x).
Korzystając z tego wykresu:
a) Zapisz w postaci przedziału zbiór wartości funkcji f,
b) Podaj wartość funkcji f dla argumentu x = 1− ,
c) Wyznacz równanie prostej BC,
d) Oblicz długość odcinka BC.
Zadanie 26. (SP07)
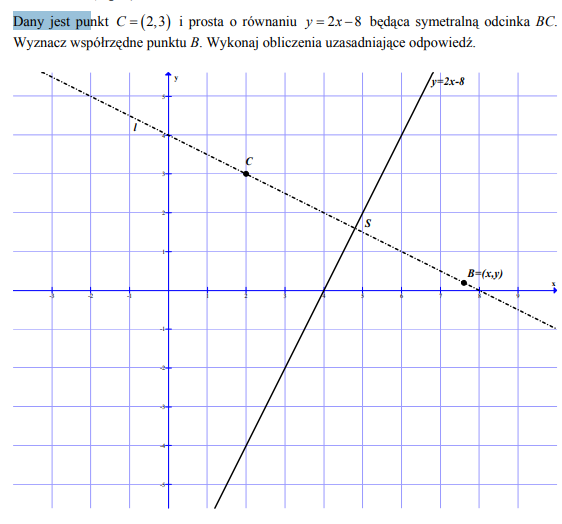
Dany jest punkt C = (2,3) i prosta o równaniu y = 2x− 8 będąca symetralną odcinka BC . Wyznacz współrzędne punktu B . Wykonaj obliczenia uzasadniające odpowiedź.