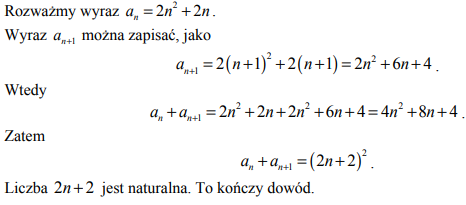Zadania maturalne z Matematyki

Tematyka: ciągli liczbowe: arytmetyczne i geometryczne.

Zadania pochodzą z oficjalnych arkuszy maturalnych CKE, które służyły przeprowadzaniu majowych egzaminów. Czteroznakowy kod zapisany przy każdym zadaniu wskazuje na jego pochodzenie: S/N – „stara”/”nowa” formuła; P/R – poziom podstawowy/rozszerzony; np. 08 – rok 2008.

Zbiór zadań maturalnych w formie arkuszy, możesz pobrać >> TUTAJ <<.

Zadanie 1. (NP15)
W rosnącym ciągu geometrycznym (a_n), określonym dla n≥1, spełniony jest warunek a₄=3a₁. Iloraz q tego ciągu jest równy:

Zadanie 2. (NP16)
W nieskończonym ciągu arytmetycznym (a_n), określonym dla n≥1, suma jedenastu początkowych wyrazów tego ciągu jest równa 187. Średnia arytmetyczna pierwszego, trzeciego i dziewiątego wyrazu tego ciągu, jest równa 12. Wyrazy a₁,a₃,a_k ciągu (a_n), w podanej kolejności, tworzą nowy ciąg – trzywyrazowy ciąg geometryczny (b_n). Oblicz k.

Zadanie 3. (NP16)
Czternasty wyraz ciągu arytmetycznego jest równy 8, a różnica tego ciągu jest równa  .Siódmy wyraz tego ciągu jest równy:

Zadanie 4. (NP16)
Ciąg (x,2x+3,4x+3) jest geometryczny. Pierwszy wyraz tego ciągu jest równy:

Zadanie 5. (NP16)
Ciąg (a_n) jest określony wzorem a_n=2n²+2n dla n≥1. Wykaż, że suma każdych dwóch kolejnych wyrazów tego ciągu jest kwadratem liczby naturalnej.

Zadanie 6. (NP17)
W ciągu arytmetycznym a_n, określonym dla n≥1, dane są: a₁=5, a₂=11. Wtedy:

Zadanie 7. (NP17)
Dany jest trójwyrazowy ciąg geometryczny (24,6,a−1). Stąd wynika, że:

Zadanie 8. (NP17)
W ciągu arytmetycznym (a_n), określonym dla n≥1, dane są: wyraz a₁=8 i suma trzech początkowych wyrazów tego ciągu S₃=33. Oblicz różnicę: a₁₆−a₁₃.

Zadanie 9. (NP18)
Dany jest ciąg (a_n) określony wzorem a_n=    dla n≥1. Ciąg ten jest:

Zadanie 10. (NP18)
Dla ciągu arytmetycznego (a_n), określonego dla n≥1, jest spełniony warunek a₄+a₅+a₆=12. Wtedy:

Zadanie 11. (NP18)
Dany jest ciąg geometryczny (a_n), określony dla n≥1, w którym a₁=, a₂=2, a₃=4, Wzór na n-ty wyraz tego ciągu ma postać:

Zadanie 12. (NP18)
Dwunasty wyraz ciągu arytmetycznego (an), określonego dla n≥1, jest równy 30, a suma jego dwunastu początkowych wyrazów jest równa 162. Oblicz pierwszy wyraz tego ciągu.

Zadanie 13. (SP15)
W ciągu arytmetycznym (a_n) określonym dla n≥1 dane są a₁=−4 i r=2. Którym wyrazem tego ciągu jest liczba 156?

 Zadanie 14. (SP15)
Dany jest skończony ciąg, w którym pierwszy wyraz jest równy 444, a ostatni jest równy 653. Każdy wyraz tego ciągu, począwszy od drugiego, jest o 11 większy od wyrazu bezpośrednio go poprzedzającego. Oblicz sumę wszystkich wyrazów tego ciągu.

Zadanie 15. (SP16)
Ciąg (a_n) jest określony wzorem a_n=2n²+2n dla n≥1. Wykaż, że suma każdych dwóch kolejnych wyrazów tego ciągu jest kwadratem liczby naturalnej.

Zadanie 16. (SP16)
W skończonym ciągu arytmetycznym (an) pierwszy wyraz a₁ jest równy 7 oraz ostatni wyraz a_n jest równy 89. Suma wszystkich wyrazów tego ciągu jest równa 2016. Oblicz, ile wyrazów ma ten ciąg.

Zadanie 17. (SP14)
Liczby 2,−1,−4 są trzema początkowymi wyrazami ciągu arytmetycznego (a_n) określonego dla liczb naturalnych n≥1. Wzór ogólny tego ciągu ma postać:

Zadanie 18. (SP14)
Liczby: x−2, 6, 12, w podanej kolejności, są trzema kolejnymi wyrazami ciągu geometrycznego. Liczba x jest równa:

Zadanie 19. (SP13)
Ciąg (27,18,x+5) jest geometryczny. Wtedy:

 Zadanie 20. (SP13)
Ciąg (a_n) określony dla n≥1 jest arytmetyczny oraz a₃=10 i a₄=14. Pierwszy wyraz tego ciągu jest równy:

Zadanie 21. (SP12)
Dany jest ciąg (a_n) określony wzorem a_n=(−1)ⁿ    ⋅   dla n≥1. Wówczas wyraz a₅ tego ciągu jest równy:

Zadanie 22. (SP12)
Ciąg (9,x,19) jest arytmetyczny, a ciąg (x,42,y,z) jest geometryczny. Oblicz x, y oraz z.

Zadanie 23. (SP11)
Dany jest nieskończony ciąg geometryczny (a_n), w którym a₃=1 i a₄=. Wtedy:

Zadanie 24. (SP11)
Dany jest nieskończony rosnący ciąg arytmetyczny (a_n) o wyrazach dodatnich. Wtedy:

Zadanie 25. (SP11)
Liczby x,y,19 w podanej kolejności tworzą ciąg arytmetyczny, przy czym x+y=8. Oblicz x i y.

Zadanie 26. (SP10)
W ciągu arytmetycznym (a_n) dane są: a₃=13 i a₅=39. Wtedy wyraz a₁ jest równy:

Zadanie 27. (SP10)
W ciągu geometrycznym (a_n) dane są: a₁=3 i a₄=24. Iloraz tego ciągu jest równy:

Zadanie 28. (SP09)
Dany jest ciąg arytmetyczny (a_n) dla n ≥ 1, w którym a₇ =1, a₁₁ = 9.

a) Oblicz pierwszy wyraz a₁ i różnicę r ciągu (a_n).
b) Sprawdź, czy ciąg (a₇,a₈,a₁₁) jest geometryczny.
c) Wyznacz takie n, aby suma n początkowych wyrazów ciągu (a_n) miała wartość najmniejszą.

Zadanie 29. (SP08)
Nieskończony ciąg liczbowy (a_n)  jest określony wzorem  a_n = 2 −   , dla n = 1,2,3,… .

a) Oblicz, ile wyrazów ciągu (a_n) jest mniejszych od 1,975.
b) Dla pewnej liczby x trzywyrazowy ciąg (a₂ ,a₇ ,x ) jest arytmetyczny. Oblicz x .

Zadanie 30. (SP07)
Dany jest ciąg arytmetyczny (a_n) , gdzie n ≥ 1 . Wiadomo, że dla każdego n ≥ 1  suma n  początkowych wyrazów S_n = a₁ + a₂ + ⋅⋅⋅+ a_n  wyraża się wzorem: S_n= −n² + 13n.

a) Wyznacz wzór na n –ty wyraz ciągu a_n .
b) Oblicz a₂₀₀₇ .
c) Wyznacz liczbę n , dla której a_n = 0 .

Zadanie 31. (SP07)
Dany jest rosnący ciąg geometryczny (a_n)  dla n ≥ 1 , w którym a₁ = x , a₂ = 14 , a₃ = y . Oblicz x  oraz y , jeżeli wiadomo, że x + y = 35.

Zadanie 32. (SP06)
Dany jest ciąg geometryczny, w którym a₁ = 12  i a₃ = 27 .

a) Wyznacz iloraz tego ciągu.
b) Zapisz wzór, na podstawie którego można obliczyć wyraz a_n, dla każdej liczby naturalnej n
c) Oblicz wyraz a₆ .

 Zadanie 33. (SP05)
Dany jest ciąg (a_n) , gdzie  dla n= 1,2,3… Wyznacz wszystkie wyrazy tego ciągu większe od .

Zadanie 34. (SP05)
Na trzech półkach ustawiono 76 płyt kompaktowych. Okazało się, że liczby płyt na półkach górnej, środkowej i dolnej tworzą rosnący ciąg geometryczny. Na środkowej półce stoją 24 płyty. Oblicz, ile płyt stoi na półce górnej, a ile płyt stoi na półce dolnej.

Zadanie 35. (SP05)
Rodzeństwo w wieku 8 i 10 lat otrzymało razem w spadku 84100 zł. Kwotę tę złożono w banku, który stosuje kapitalizację roczną przy rocznej stopie procentowej 5%. Każde z dzieci otrzyma swoją część spadku z chwilą osiągnięcia wieku 21 lat. Życzeniem spadkodawcy było takie podzielenie kwoty spadku, aby w przyszłości obie wypłacone części spadku zaokrąglone do 1 zł były równe. Jak należy podzielić kwotę 84100 zł między rodzeństwo? Zapisz wszystkie wykonywane obliczenia.