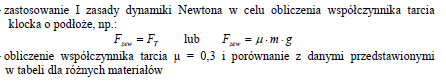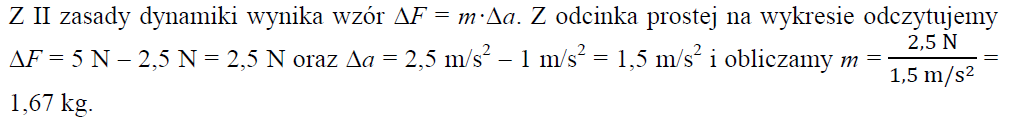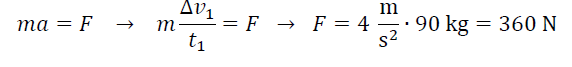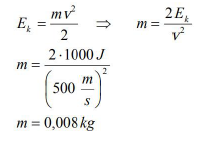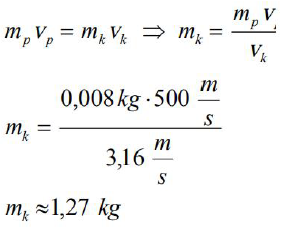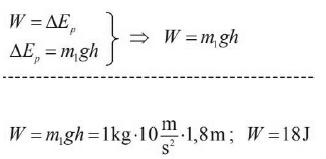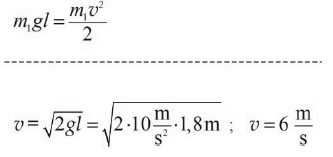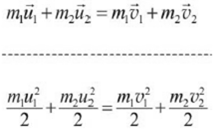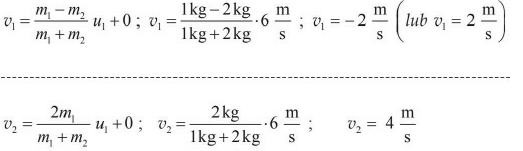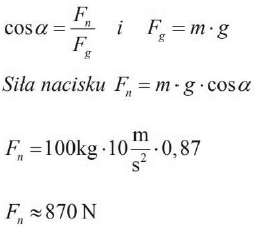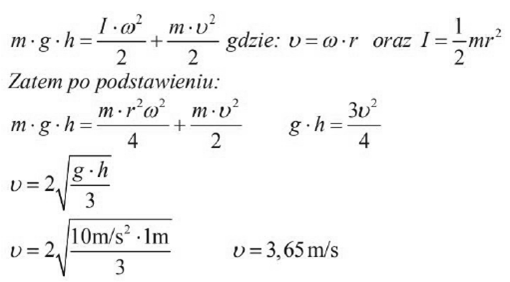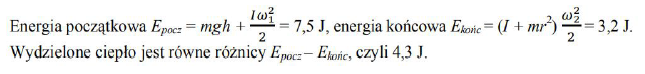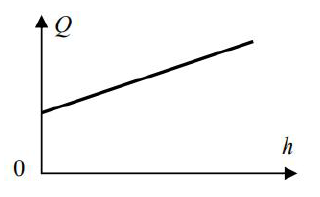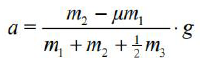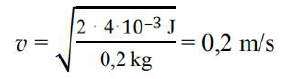Zadania maturalne z Fizyki
Temat: Dynamika
Zadania pochodzą z oficjalnych arkuszy maturalnych CKE, które służyły przeprowadzaniu majowych egzaminów. Czteroznakowy kod zapisany przy każdym zadaniu wskazuje na jego pochodzenie: S/N – „stara”/”nowa” formuła; P/R – poziom podstawowy/rozszerzony; np. 08 – rok 2008.
Zbiór zadań maturalnych w formie arkuszy, możesz pobrać >> TUTAJ <<.
Zadanie 1. (SP06)
Stosowana przez Izaaka Newtona metoda badawcza, polegająca na wykonywaniu doświadczeń, zbieraniu wyników swoich i cudzych obserwacji, szukaniu w nich regularności, stawianiu hipotez, a następnie uogólnianiu ich poprzez formułowanie praw, to przykład metody
- indukcyjnej.
- hipotetyczno-dedukcyjnej.
- indukcyjno-dedukcyjnej.
- statystycznej.
Zadanie 2. (SP06)
Drewniany klocek przymocowany jest do ściany za pomocą nitki, która wytrzymuje naciąg siłą o wartości 4 N. Współczynnik tarcia statycznego klocka o podłoże wynosi 0,2. W obliczeniach przyjmij, że wartość przyspieszenia ziemskiego jest równa 10 m/s2.
2.1
Oblicz maksymalną wartość powoli narastającej sily F z jakąmożna poziomo ciągnąć klocek, by nitka nie uległa zerwaniu.
2.2
Oblicz wartość przyspieszenia, z jakim będzie poruszał się klocek, jeżeli usunięto nitkę łączącą klocek ze ścianą, a do klocka przyłożono poziomo skierowaną siłę o stałej wartości 6 N. Przyjmij, że wartość siły tarcia kinetycznego jest równa 1,5 N.
2.1
2.2
Zadanie 3. (SP06)
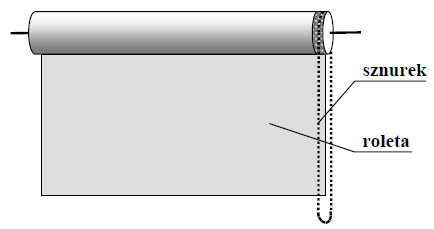
Roleta okienna zbudowana jest z wałka, na którym nawijane jest płótno zasłaniające okno (rys). Roletę można podnosić i opuszczać za pomocą sznurka obracającego wałek.
3.1
Wyjaśnij, dlaczego w trakcie podnoszenia rolety ruchem jednostajnym, siła z jaką trzeba ciągnąć za sznurek nie jest stała. Przyjmij, że średnica wałka nie zależy od ilości płótna nawiniętego na wałek oraz pomiń siły oporu ruchu.
Podczas podnoszenia rolety ruchem jednostajnym ciężar/masa jej zwisającej części maleje i dlatego wartość siły z jaką trzeba ciągnąć za sznurek zmniejsza się.
Zadanie 4. (SP07)
Spadochroniarz o masie 75 kg opada na spadochronie pionowo w dół z prędkością o stałej wartości 5 m/s. Siła oporów ruchu ma wartość około
- 25 N.
- 75 N.
- 250 N.
- 750 N.
Zadanie 5. (SP07)
Lokomotywa manewrowa pchnęła wagon o masie 40 ton nadając mu początkową prędkość o wartości 5 m/s. Wagon poruszając się ruchem jednostajnie opóźnionym zatrzymał się po upływie 20 s. Oblicz wartość siły hamującej wagon.
Zadanie 6. (SP08)
Fragment balkonu o masie 0,5 kg oderwał się i spadł z wysokości 5 m. W obliczeniach przyjmij, że wartość przyspieszenia ziemskiego wynosi 10 m/s2.
6.2
W rzeczywistości podczas spadania działa siła oporu i oderwany element balkonu spadał przez 1,25 s ruchem przyspieszonym, uderzając w podłoże z prędkością o wartości 8 m/s. Oblicz wartość siły oporu, przyjmując, że podczas spadania była ona stała.
Zadanie 7. (SP08)
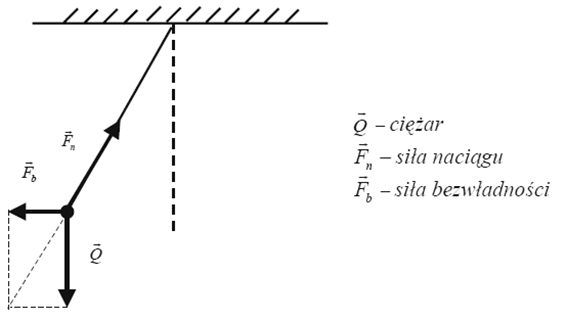
Podczas gwałtownego awaryjnego hamowania tramwaju uchwyt do trzymania się, zamocowany pod sufitem wagonu, odchylił się od pionu o kąt 15o. Załóż, że tramwaj poruszał się po poziomej powierzchni ruchem jednostajnie opóźnionym, prostoliniowym. W obliczeniach przyjmij, że wartość przyspieszenia ziemskiego wynosi 10 m/s2.
7.1
Narysuj, oznacz i nazwij siły działające na swobodnie wiszący uchwyt podczas hamowania.
7.2
Oblicz wartość opóźnienia tramwaju podczas hamowania.
7.1
7.2
Zadanie 8. (SP09)
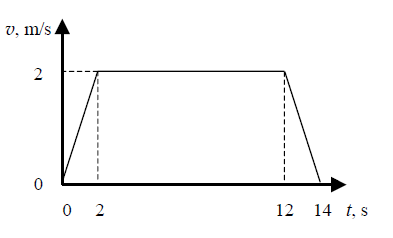
Człowiek o masie 60 kg stoi w windzie, która rusza z miejsca i porusza się w górę. Wykres przedstawia zależność wartości prędkości szybkobieżnej windy od czasu.
8.1
Oblicz wartość średniej prędkości windy podczas trwania całego ruchu.
8.2
Oblicz wartość siły nacisku człowieka na podłogę windy w ciągu dwóch pierwszych sekund ruchu. Przyjmij, że wartość przyspieszenia ziemskiego wynosi 10 m/s2.
8.3
Narysuj, oznacz i nazwij siły działające na człowieka w windzie (w układzie nieinercjalnym, związanym z windą) podczas ruszania windy. Uwzględnij na rysunku odpowiednie długości wektorów, a człowieka potraktuj jak punkt materialny.
8.1
8.2
8.3
Zadanie 9. (SP09)
W pracowni fizycznej uczniowie wyznaczali współczynnik tarcia statycznego drewna o drewno. Dysponowali siłomierzem, drewnianym klockiem z haczykiem oraz poziomo ustawioną drewnianą deską. Ustal, jakie wielkości fizyczne powinni zmierzyć uczniowie w tym doświadczeniu. Zapisz ich pełne nazwy.
Zdający może zapisać w odpowiedzi: ciężar klocka i maksymalna siła tarcia.
Zadanie 10. (SP10)
Z wysokości 20 m upuszczono swobodnie mały kamień.
10.1
Uzupełnij/dokończ zdanie:
Zjawisko swobodnego spadku w ziemskim polu grawitacyjnym występuje wtedy, gdy prędkość początkowa jest równa zero oraz ………………………………………………………
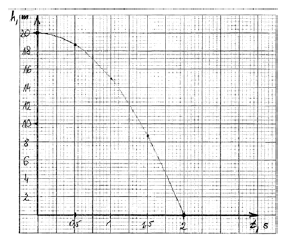
10.2
Wykonaj wykres ilustrujący zależność wysokości, na jakiej znajduje się kamień, od czasu spadania. Na wykresie nanieś 5 wartości liczbowych wysokości (w przedziale czasu 0–2 s). Wykonaj niezbędne obliczenia.
10.1
… gdy nie występują siły oporu lub … gdy jedyną siłą działającą na ciało jest siła grawitacji.
10.2
– obliczenie wysokości, na której znajduje się kamień (np.: 18,75 m; 15 m; 8,75 m; 0 m) lub przebytej drogi przez kamień (np.: 1,25 m; 5 m; 11,25 m; 20 m)
– opisanie i wyskalowanie osi (z uwzględnieniem wysokości)
– naniesienie punktów o odpowiednich współrzędnych na wykresie (np.: 0 s, 20 m; 0,5 s, 18,75 m; 1 s, 15 m; 1,5 s, 8,75 m; 2 s, 0 m)
– narysowanie krzywej
Zadanie 11. (SP10)
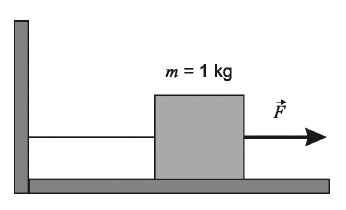
Klocek o masie 1 kg przesuwano po poziomej powierzchni ruchem jednostajnym, działając na niego siłą o wartości 3 N.
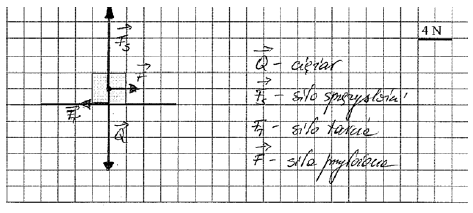
11.1
Narysuj wektory wszystkich sił działających na klocek. Oznacz je i zapisz ich nazwy. Rysunek wykonaj z zachowaniem skali, zaznaczając punkty przyłożenia sił.
11.2
Wykaż, wykonując odpowiednie obliczenia, że spośród czterech par materiałów wymienionych w poniższej tabeli, klocek i podłoże, po którym się porusza, wykonane są z drewna.
11.1
- narysowanie, oznaczenie i poprawne nazwanie wszystkich sił poziomych (np.: siła tarcia, siła zewnętrzna)
- narysowanie, oznaczenie i poprawne nazwanie wszystkich sił pionowych (np.: ciężar, siła sprężystości podłoża)
11.2
Zadanie 12. (SP11)
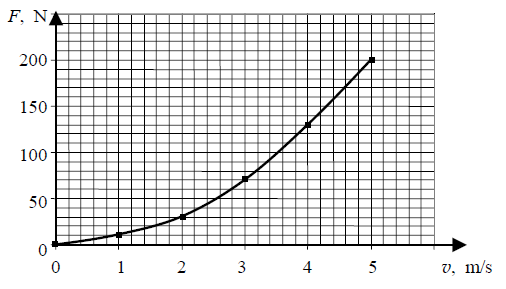
Jadąc z rosnącą prędkością, rowerzysta odczuwa zwiększający się opór powietrza. Poniższa
tabela przedstawia zmierzone wartości oporu powietrza dla różnych prędkości.
12.1
Wykonaj wykres zależności siły oporu powietrza od prędkości rowerzysty.
12.2
Zapisz, przy jakiej prędkości siła oporu powietrza będzie miała wartość 100 N.
12.3
Co powinien zrobić rowerzysta, aby przy danej prędkości zmniejszyć opór powietrza?
12.1
12.2
Opór o wartości 100 N będzie przy prędkości ok. 3,5 m/s.
12.3
Przykłady poprawnej odpowiedzi
- Powinien się pochylić
- Powinien nałożyć gładki ubiór
- Powinien nałożyć opływowy kask
- Powinien przyjąć bardziej aerodynamiczną postawę
- Powinien zmniejszyć powierzchnię oporu
Zadanie 13. (SP12)
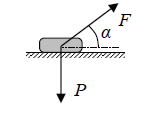
Jasio ciągnie zabawkę o ciężarze P za sznurek skierowany pod kątem α do podłogi. Siła
napięcia sznurka wynosi F, a współczynnik tarcia zabawki o podłogę jest równy μ. Aby
rozstrzygnąć, czy zabawka ruszy z miejsca, należy porównać ze sobą wielkości
- μF oraz P cos α.
- μ(P – F) oraz F sin α.
- μP oraz (P – F) sin α.
- μ(P – F sin α) oraz F cos α.
Zadanie 14. (SP12)
Pocisk o masie 10 g lecący poziomo z prędkością 600 m/s wpada do pudła z piaskiem o masie 5 kg i grzęźnie w nim. Pudło początkowo spoczywało na poziomym podłożu. Współczynnik tarcia pudła o podłoże wynosi 0,3.
14.1
Oblicz prędkość pudła wraz z pociskiem tuż po ugrzęźnięciu pocisku (zatrzymaniu ruchu względnego). Wskazówka: ponieważ ugrzęźnięcie pocisku trwa bardzo krótko, więc można zaniedbać skutki działania siły tarcia pudła o podłoże w ciągu tego czasu.
14.2
Przyjmując prędkość pudła z pociskiem tuż po ugrzęźnięciu pocisku równą 1 m/s, oblicz odległość, na jaką przemieści się ono do chwili zatrzymania.
14.1
14.2
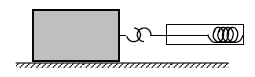
Zadanie 15. (SP12)
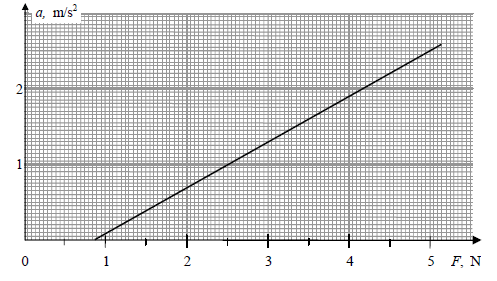
Uczniowie położyli na stole klocek, do którego doczepili siłomierz (rys.). Działając na klocek stałą siłą wprawili go w ruch i mierzyli jego przyspieszenie a. Doświadczenie powtórzyli kilka razy przy różnych wartościach siły F wywieranej przez siłomierz, a wyniki przedstawiono na poniższym wykresie.
15.1
Napisz wartość przyspieszenia klocka, gdy siła F wynosi 0,5 N. Uzasadnij odpowiedź.
15.2
Na podstawie wykresu można wyznaczyć siłę tarcia T działającą na klocek w czasie jego ruchu. Podaj wartość T i uzasadnij ten wynik.
15.3
Na podstawie wykresu można wyznaczyć masę klocka m. Oblicz wartość m, stosując odpowiednie zależności.
15.1
Przyspieszenie jest równe zero, gdyż – jak można odczytać z wykresu – siła o wartości 0,5 N nie wystarcza do ruszenia klocka z miejsca.
15.2
Siła tarcia wynosi 0,9 N, gdyż jeśli jest ona równa co do wartości sile F, to przyspieszenie wynosi 0.
15.3
Zadanie 16. (SP13)
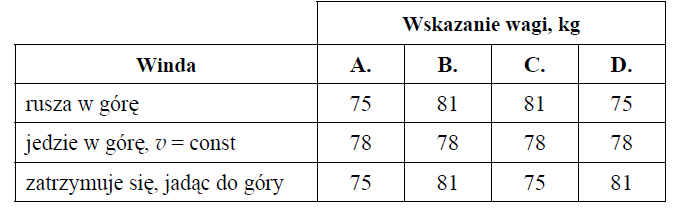
W windzie znajduje się waga łazienkowa (naciskowa), na której stoi człowiek. Zanotowano wskazania wagi podczas ruchu windy. W tabeli wybierz kolumnę, w której dane są zgodne z prawami mechaniki.
Zadanie 17. (SP14)
Na sanki o masie 2 kg poruszające się z prędkością o wartości 6 m/s zaczęła działać stała siła hamująca, która zatrzymała te sanki w czasie 4 s. Wartość siły hamującej wynosi około
A. 1,5 N.
B. 3 N.
C. 4 N.
D. 6 N.
Zadanie 18. (SP14)
Winda jedzie 15 sekund z parteru na trzecie piętro bez zatrzymywania się. Przez pierwsze 2 sekundy winda porusza się ruchem jednostajnie przyspieszonym, potem – ruchem jednostajnym, a przez 2 ostatnie sekundy przed zatrzymaniem – ruchem jednostajnie opóźnionym. Wartości przyspieszenia i opóźnienia windy wynoszą 0,5 m/s2
18.1
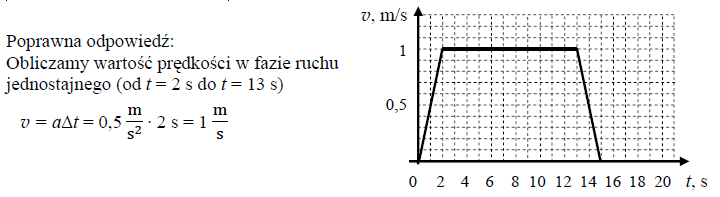
Narysuj wykres zależności wartości prędkości windy od czasu.
18.2
Oblicz wartość siły reakcji podłogi windy działającej na człowieka o masie 65 kg w ciągu pierwszych dwóch sekund ruchu.
18.1
18.2
Zadanie 19. (NP15)
Kulka zawieszona na sznurku porusza się ruchem jednostajnym po okręgu w płaszczyźnie poziomej. Podczas tego ruchu
- ani wektor pędu kulki, ani jej energia kinetyczna się nie zmieniają.
- zarówno wektor pędu kulki, jak i jej energia kinetyczna się zmieniają.
- nie zmienia się wektor pędu kulki, a zmienia się jej energia kinetyczna.
- nie zmienia się energia kinetyczna kulki, a zmienia się wektor jej pędu.
Zadanie 20. (NP17)
Rowerzysta jadący początkowo z prędkością 8 m/s rozpoczął zjazd z górki i przyśpieszył jednostajnie wzdłuż prostego zbocza do prędkości 10 m/s w czasie 4 sekund. Jeżeli łączna masa rowerzysty i roweru była równa 60 kg, to siła wypadkowa powodująca przyśpieszenie była równa
A. 30 N
B. 120 N
C. 150 N
D. 270 N
Zadanie 21. (NP18)
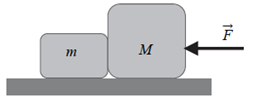
Zestaw dwóch klocków o masach m = 1kg oraz M = 4 kg jest pchany jeden za drugim po poziomym podłożu siłą F (zobacz rysunek). W wyniku tego układ dwóch klocków uzyskał przyspieszenie o wartości 0,4 m/s2. Doświadczenie to jest wykonywane na powierzchni Ziemi, a współczynnik tarcia pomiędzy każdym z klocków i podłożem wynosi 0,2.
Wartość siły reakcji z jaką klocek o masie M działa na klocek o masie m, wynosi około:
A. 10 N
B. 2 N
C. 2,4 N
D. 0,4 N
Zadanie 22. (NP18)
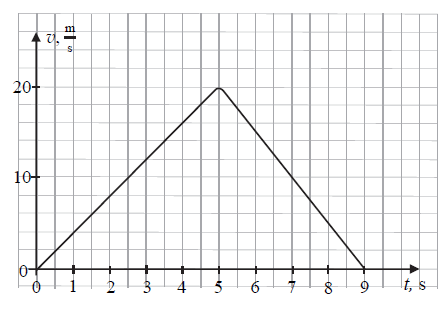
Motocykl ruszył ze skrzyżowania i po 9 sekundach zatrzymał się przed następnym skrzyżowaniem. Na wykresie obok przedstawiono zależność wartości prędkości motocykla od czasu trwania tego ruchu. Przejazd od jednego do drugiego skrzyżowania odbywał się po prostym, poziomym odcinku jezdni, a kierujący pojazdem ma masę 90 kg.
Oblicz wartość poziomej składowej siły, z jaką motocykl działa na motocyklistę w czasie ruchu przyspieszonego (do piątej sekundy). Załóż, że ciało motocyklisty jest skryte za osłoną tak, że siły oporów powietrza działają tylko na tę osłonę i motocykl – tzn. działanie sił oporów na ciało motocyklisty możemy pominąć.
Motocyklista ma takie samo przyspieszenie względem jezdni, jakie ma motocykl, na którym nieruchomo siedzi. Zgodnie z założeniem o pominięciu sił oporów działających na motocyklistę, to siła wypadkowa działająca na niego będzie siłą, z jaką działa nań motocykl. Siłę wypadkową obliczamy z drugiej zasady dynamiki:
Zadanie 23. (NP19)
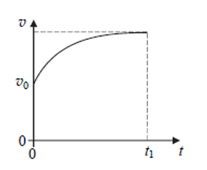
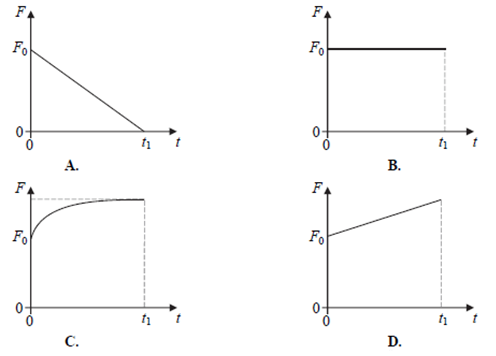
Na ciało poruszające się wzdłuż linii prostej działa siła wypadkowa F. Kierunek i zwrot siły F jest taki sam jak kierunek i zwrot prędkości v ciała. Na rysunku obok przedstawiono wykres zależności wartości prędkości ciała od czasu (od chwili t = 0 do chwili t = t1) – gdy na ciało działa siła. Osie na rysunkach są wyskalowane liniowo.
Poprawną zależność wartości siły wypadkowej od czasu (od chwili t = 0 do chwili t = t1) przedstawia wykres.
Zadanie 24 (SR05)
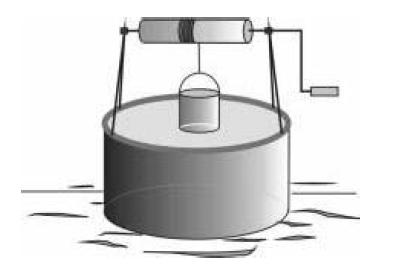
Kołowrót w kształcie walca, którego masa wynosi 10 kg, zamocowany jest nad studnią (rys.).
Na kołowrocie nawinięta jest nieważka i nierozciągliwa linka, której górny koniec przymocowany jest do kołowrotu. Do dolnego końca linki przymocowano wiadro o masie 5 kg, służące do wyciągania wody ze studni.
24.1
Pod wpływem ciężaru pustego wiadra linka rozwija się, powodując ruch obrotowy kołowrotu. Narysuj siły działające w tym układzie oraz oblicz przyspieszenie wiadra. Moment bezwładności walca względem osi obrotu wyraża się wzorem:
Pomiń wpływ sił oporu ruchu oraz korby z rączką na wartość przyspieszenia.

24.2
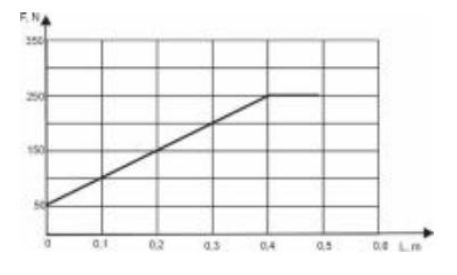
Po nabraniu wody, wiadro ze stanu pełnego zanurzenia (rys.), jest wyciągane ze studni ruchem jednostajnym. Narysuj wykres zależności wartości F sił y naciągu linki od drogi L przebytej przez górny brzeg wiadra ponad lustrem wody w studni. Masa wiadra wypełnionego wodą jest równa 25 kg. Wiadro ma kształt walca o wysokości 0,4 m. Pomijamy objętość blachy, z której zrobione jest wiadro. Poziom wody w studni nie ulega zmianom. Przyjmij przyśpieszenie ziemskie g = 10 m/s2.
24.3
Wyjaśnij, dlaczego parcie wody na dno podczas wyciągania wiadra wypełnionego wodą ze studni ruchem przyspieszonym jest większe niż podczas wyciągania wiadra ruchem jednostajnym.
24.1
Narysowanie sił działających na układ.
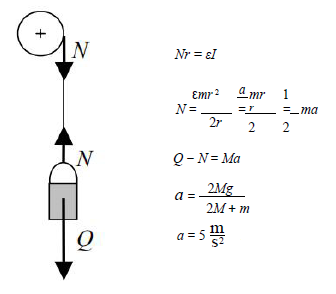
24.2
24.3
Poruszające się ruchem zmiennym wiadro z wodą jest układem nieinercjalnym. W tym układzie działa jeszcze siła bezwładności, mająca ten sam zwrot co siła ciężkości. Siła parcia, będąca wypadkową tych sił, ma większą wartość niż podczas ruchu jednostajnego.
Zadanie 25. (SR06)
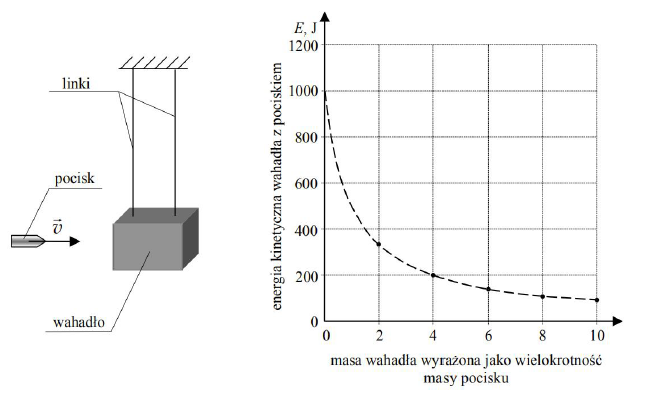
Na rysunku poniżej przedstawiono schematycznie urządzenie do pomiaru wartości prędkości pocisków wystrzeliwanych z broni palnej. Podstawowym elementem takiego urządzenia jest tzw. wahadło balistyczne będące (w dużym uproszczeniu) zawieszonym na linkach klockiem, w którym grzęzną wystrzeliwane pociski. Po trafieniu pociskiem wahadło wychyla się z położenia równowagi i możliwy jest pomiar jego energii kinetycznej.
Punkty na wykresie przedstawiają zależność energii kinetycznej klocka wahadła z pociskiem (który w nim ugrzązł) tuż po uderzeniu pocisku, od masy klocka. Pomiary wykonano dla 5 klocków o różnych masach (linia przerywana przedstawia zależność teoretyczną). Wartość prędkości pocisku, tuż przed trafieniem w klocek wahadła, za każdym razem wynosiła 500 m/s, a odległość od środka masy klocka wahadła do punktu zawieszenia wynosiła 1 m. W obliczeniach pomiń masę linek mocujących klocek wahadła.
25.1
Wykaż, analizując wykres, że masa pocisku jest równa 0,008 kg.
25.2
Oblicz wartość prędkości klocka z pociskiem bezpośrednio po zderzeniu w sytuacji, gdy masa klocka była 499 razy większa od masy pocisku.
25.3
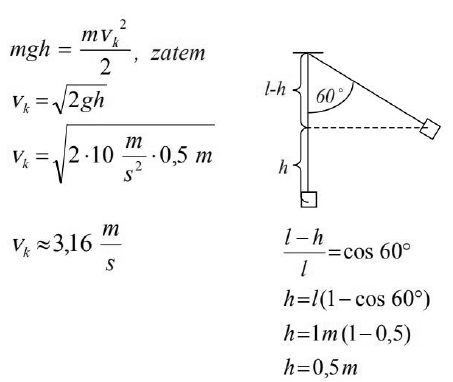
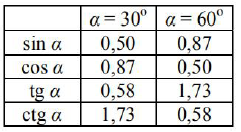
Oblicz, jaka powinna być masa klocka wahadła, aby po wychyleniu z położenia równowagi wahadła o 60o , zwolnieniu go, a następnie trafieniu pociskiem w chwili przechodzenia wahadła przez położenie równowagi, wahadło zatrzymało się w miejscu. Do obliczeń przyjmij, że masa pocisku wynosi 0,008 kg. W obliczeniach możesz skorzystać z podanych poniżej wartości funkcji trygonometrycznych.
25.1
Analizując wykres można zauważyć, że dla masy klocka równej 0 , energia kinetyczna wahadła z pociskiem jest równa 1000 J.
25.2
25.3
Aby wahadło zatrzymało się w miejscu wartości pędów pocisku i klocka muszą być równe.
Korzystając z zasady zachowania energii
Zadanie 26.
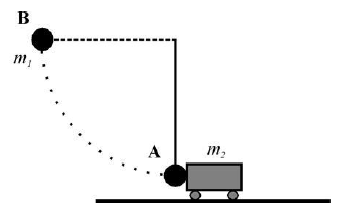
Stalowa kulka o masie 1 kg, wisząca na nici o długości 1,8 m została odchylona od pionu o kąt 90o wzdłuż łuku AB, a następnie zwolniona (rys.). Po zwolnieniu uderzyła w spoczywający stalowy wózek, który zaczął poruszać się po szynach praktycznie bez tarcia. Masa wózka wynosi 2 kg. Przyjmij, że zderzenie ciał było doskonale sprężyste.
26.1
Oblicz pracę , jaką trzeba wykonać powoli odchylając pionowo wiszącą kulkę z położenia A do położenia B.
26.2
Wykaż, że wartość prędkości kulki w chwili uderzenia w wózek wynosi 6 m/s.
26.3
Oblicz wartość siły naciągu nici w momencie gdy kulka uderza w wózek. Przyjmij, że wartość prędkości kulki podczas uderzenia w wózek wynosi 6 m/s.
26.4
Zapisz, korzystając z przyjętych powyżej oznaczeń, równania wynikające z zasad zachowania, które powinny być zastosowane do opisu zderzenia kulki z wózkiem (pozwalające wyprowadzić powyższe zależności).
26.5
Oblicz wartości prędkości jakie uzyskają wózek i kulka w wyniku zderzenia. Wykorzystaj wzory podane w treści zadania. Przyjmij, że kulka uderza w wózek z prędkością o wartości 6 m/s.
26.6
Wózek po uderzeniu kulki odjeżdża, natomiast kulka zaczyna poruszać się ruchem drgającym, w którym nić podczas maksymalnego wychylenia tworzy z pionem kąt 27ᵒ. Podaj, czy w opisanej sytuacji można dokładnie obliczyć okres wahań takiego wahadła korzystając z zależności
Odpowiedź uzasadnij.
26.1
26.2
26.3
26.4
26.5
26.6
W opisanej sytuacji nie można dokładnie obliczyć okres wahań takiego wahadła.
Zależność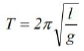
Zadanie 27. (SR08)
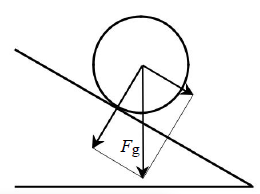
Do hurtowni chemicznej przywieziono transport blaszanych beczek z gipsem. W celu wyładowania beczek z samochodu położono pochylnię, tworząc w ten sposób równię pochyłą. Wysokość, z jakiej beczki staczały się swobodnie bez poślizgu wynosiła 100 cm. Beczki były ściś le wypełnione gipsem, który nie mógł się przemieszczać, i miały kształt walca o średnicy 40 cm. Masa gipsu wynosiła 100 kg.
W obliczeniach przyjmij wartość przyspieszenia ziemskiego równą 10 m/s2, a beczkę potraktuj jak jednorodny walec. Masę blachy, z której wykonano beczkę pomiń.
Moment bezwładności walca, obracającego się wokół osi prostopadłej do podstawy walca i przechodzącej przez jej środek, jest równy I = mr 2 .
27.1
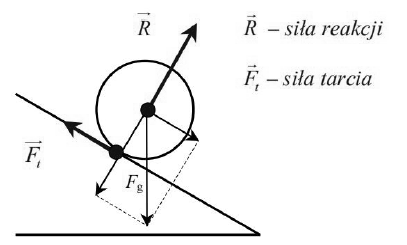
Uzupełnij rysunek o pozostałe siły działające na beczkę podczas jej swobodnego staczania.
Zapisz ich nazwy.
27.2
Oblicz wartość siły nacisku beczki na równię podczas staczania, jeżeli kąt nachylenia pochylni do poziomu wynosi 30o.
27.3
Wykaż, że wartość prędkości liniowej beczki po stoczeniu się z pochylni jest równa 3,65 m/s.
27.4
Oblicz, korzystając ze związku pomiędzy energią i pracą, zasięg toczenia się beczki po poziomej trawiastej powierzchni. Przyjmij, że podczas toczenia się beczki po trawie działa na nią stała siła oporu o wartości 50 N, a wartość prędkości liniowej beczki po stoczeniu się z pochylni jest równa 3,65 m/s.
27.5
Wykaż, że zmiana zawartości beczki z gipsu na cement (o innej niż gips masie), również ściśle wypełniający beczkę, nie spowoduje zmiany wartości przyspieszenia kątowego, z jakim obraca się beczka wokół osi prostopadłej do podstawy beczki i przechodzącej przez jej środek.
27.1
27.2
27.3
27.4
27.5
Moment siły
jest funkcją ciężaru beczki i jest wprost proporcjonalny do masy (M ~ m). Moment bezwładności walca I jest wprost proporcjonalny do masy (I ~ m). Ponieważ ε =
zatem wartość przyspieszenia kątowego ε nie zależy od masy.
Zadanie 28. (SR12)
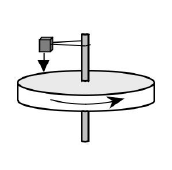
Krążek o momencie bezwładności 0,01 kg·m2 obracał się bez tarcia wokół swojej osi z prędkością kątową 32 rad/s. Na ten krążek spadł ciężarek o masie 0,6 kg, upuszczony bez prędkości początkowej. Ciężarek był połączony z osią krążka nitką ślizgającą się po osi bez tarcia. Po chwili ciężarek zaczął obracać się razem z krążkiem, pozostając w odległości 10 cm od osi obrotu. Rozmiary ciężarka można pominąć.
28.1
Napisz nazwę zasady zachowania, która pozwala wyznaczyć wspólną prędkość kątową krążka i ciężarka. Oblicz wartość tej prędkości kątowej.
28.2
Współczynnik tarcia ciężarka o krążek wynosi 0,3. Ponadto zakładamy, że można pominąć efekty uderzenia przy upadku (tzn. przyjąć, że wysokość spadku była bardzo mała). Korzystając z powyższych informacji, wyprowadź wzór na moment siły oddziaływania ciężarka na krążek oraz oblicz, po jakim czasie od upadku ciężarka jego poślizg ustał i prędkość kątowa krążka osiągnęła wartość końcową 20 rad/s.
28.3
Początkowo ciężarek znajdował się na wysokości 40 cm nad krążkiem. Oblicz całkowitą energię mechaniczną układu:
- w sytuacji początkowej
- po upadku ciężarka oraz zmniejszeniu prędkości kątowej krążka do wartości 20 rad/s.
Oblicz ciepło wydzielone w czasie upadku.
28.4
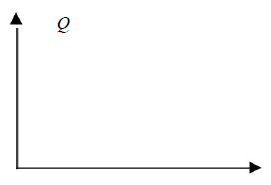
Doświadczenie opisane w informacji wstępnej wykonano kilkakrotnie, zmieniając wysokość spadku ciężarka. Naszkicuj wykres zależności wydzielonego ciepła Q od wysokości spadku h. Na wykresie nie nanoś wartości liczbowych.
28.1.
Jest to zasada zachowania momentu pędu. W opisanej sytuacji Iω1 = (I + mr2)ω2, a po podstawieniu danych obliczamy ω2 = 20 rad/s (lub 20 s–1).
28.2.
28.3.
28.4.
Zadanie 29. (SR13)
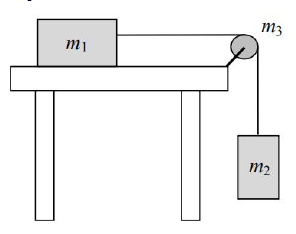
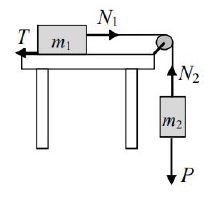
Do krawędzi stołu przymocowany jest blok nieruchomy, będący jednorodnym krążkiem o masie m3, obracającym się bez tarcia. Przez blok przełożona jest bardzo lekka i nierozciągliwa linka, której jeden koniec doczepiony jest do skrzynki o masie m1, a drugi – do skrzynki o masie m2. Pierwsza skrzynka leży na stole, a druga wisi na lince (rys. poniżej). Współczynnik tarcia pierwszej skrzynki o stół oznaczamy jako μ (bez rozróżnienia współczynników tarcia statycznego i kinetycznego). Moment bezwładności jednorodnego krążka (lub walca) względem jego osi wyraża się wzorem , gdzie R jest promieniem krążka, a m – jego masą. W chwili początkowej obie skrzynki były nieruchome.
29.1
Skrzynki zaczęły się poruszać. Dorysuj i opisz wektory sił działających na obydwie skrzynki wzdłuż ich kierunków ruchu.
29.2
Wykaż, że podczas ruchu skrzynek ich przyspieszenie można wyrazić wzorem
Skorzystaj ze wzorów wyrażających II zasadę dynamiki dla bloku, pierwszej i drugiej skrzynki.
29.3
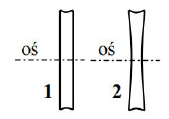
Blok zastąpiono innym – o tej samej masie i promieniu, ale cieńszym bliżej osi, a grubszym na obrzeżu. Oba bloki są wykonane z jednorodnego materiału, a obok zostały przedstawione w przekroju. Określ, czy zastąpienie bloku 1 przez blok 2 spowodowało wzrost przyspieszenia układu, czy spadek, czy też przyspieszenie się nie zmieniło. Uzasadnij odpowiedź.
29.4
Oblicz wartość przyspieszenia określonego wzorem z zadania 6.2 dla następujących danych:
m1 = 2 kg, m2 = 0,4 kg, m3 = 0,5 kg, μ = 0,3.
Zinterpretuj otrzymany wynik, uwzględniając fakt, że skrzynki początkowo spoczywały.
29.5
Oznaczmy przez N1 siłę napięcia poziomego odcinka linki, a przez N2 – siłę napięcia pionowego odcinka linki. Podkreśl właściwe wyrażenia w poniższych zdaniach.
Gdy układ pozostaje w równowadze, siła N1 jest ( większa od siły N2 / mniejsza od siły N2 / równa sile N2 ).
Jeśli wisząca skrzynka (o masie m2) zaczęła opadać, to siła N1 jest ( większa od siły N2 / mniejsza od siły N2 / równa sile N2 ).
29.1.
Na rysunku T jest siłą tarcia, N1 i N2 – siłami naciągu linki (dopuszcza się brak rozróżnienia sił N1 i N2), a P – siłą ciężkości.
29.2.
29.3.
Przyspieszenie układu zmalało, co wynika ze wzrostu momentu bezwładności bloku.
Odp.:
29.4.
Z podstawienia danych otrzymujemy a = –0,74 m/s, co oznacza, że w rzeczywistości układ nie zaczyna się poruszać (a = 0).
29.5.
Podkreślenie w pierwszym zdaniu równa sile N2, a w drugim mniejsza od siły N2.
Zadanie 30. (SR14)
Na ciała spadające w powietrzu działa siła oporu zależna od prędkości. Wartość tej siły najczęściej obliczamy ze wzoru 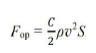
Podczas spadania ciał wraz ze wzrostem prędkości rośnie siła oporu, aż do zrównoważenia ciężaru ciała, kiedy dalszy ruch odbywa się ze stałą prędkością.
30.1
Piłeczka pingpongowa ma masę 2,5 g, a jej promień wynosi 1,7 cm. Gęstość powietrza jest równa 1,3 kg/m. Oblicz prędkość, przy której taka piłeczka będzie spadać ruchem jednostajnym.
30.2
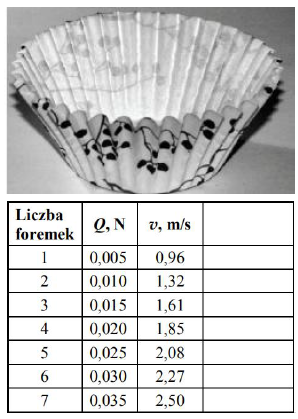
Aby sprawdzić, jak siła oporu powietrza zależy od prędkości, użyto papierowych foremek do ciastek o masie 0,5 g każda.
Doświadczenie polegało na wkładaniu jednej foremki w drugą i pomiarze prędkości v jednostajnego spadku zestawu foremek.
Zakładamy, że cały ruch odbywa się ze stałą prędkością (rozpędzanie foremek do tej prędkości trwa bardzo krótko). Gdy łączymy foremki, zmieniamy ciężar zestawu Q, natomiast nie zmienia się pole poprzecznego przekroju S. Wyniki przedstawiono w poniższej tabeli.
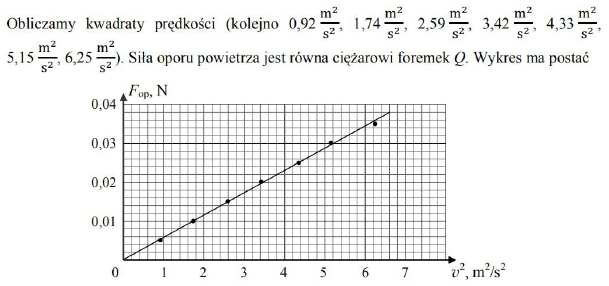
Na podstawie wyników doświadczenia wykonaj wykres zależności siły oporu od kwadratu prędkości foremek. Do zapisu obliczeń możesz wykorzystać wolną kolumnę w tabeli.
Wyjaśnij, dlaczego wykres świadczy o proporcjonalności siły oporu do kwadratu prędkości foremek.
30.1
30.2
Położenie punktów na wykresie jest zgodne z linią prostą przechodzącą przez początek układu współrzędnych, co świadczy o zależności proporcjonalnej między wielkościami odłożonymi na osiach.
Zadanie 31. (NR15)
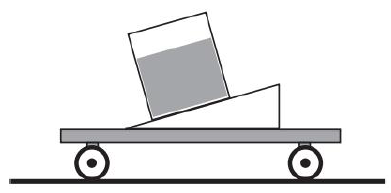
Uczniowie w pracowni fizycznej wykonali następujące doświadczenie. Na wózku zamontowali równię pochyłą, na której zamocowali naczynie z wodą i wprawili wózek w ruch jednostajny prostoliniowy po poziomej powierzchni. Gdy na wózek zaczęła działać dodatkowa siła, po pewnym czasie powierzchnia wody stała się równoległa do powierzchni równi, jak na rysunku obok.
Dokończ poniższe zdanie. Zaznacz właściwe uzupełnienia wybrane spośród A i B oraz spośród 1–3.
Takie ustawienie powierzchni wody jest możliwe, gdy dodatkowa siła działająca na wózek była skierowana
B – 3.
Zadanie 32. (NR15)
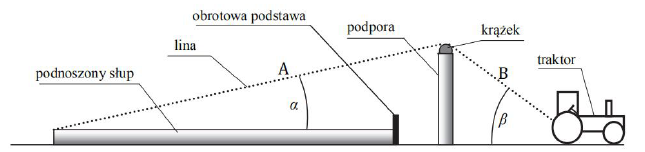
Słupy energetyczne linii przesyłowych wysokiego napięcia można składać z części na powierzchni ziemi, a następnie podnosić je do pozycji pionowej za pomocą liny, podpory z obrotowym krążkiem i na przykład traktora. Do wierzchołka leżącego słupa przyczepia się jeden z końców liny i przerzuca ją przez podporę, natomiast drugi koniec liny jest ciągnięty przez traktor. Drugi koniec słupa opiera się o zakotwiczoną w ziemi obrotową podstawę (rysunek poniżej). Zakładamy, że krążek na podporze obraca się bez tarcia.
32.1.
Oceń prawdziwość poniższych zdań. Zaznacz P, jeśli zdanie jest prawdziwe, lub F – jeśli zdanie jest fałszywe.
- Podczas powolnego podnoszenia słupa siła naciągu liny w części A ma inną wartość niż siła naciągu liny w części B. P F
- W początkowej fazie podnoszenia słupa kąt β między liną a poziomem maleje. P F
- Przy niezmiennej wysokości podpory i niezmiennym położeniu obrotowej podstawy siła naciągu liny konieczna do uniesienia słupa z pozycji poziomej zależy od wysokości (długości) słupa. P F
32.2.
Masa słupa wynosi 2000 kg, a kąt α jest równy 15°. Przyjmujemy, że środek masy słupa znajduje się w połowie jego długości.
Oblicz minimalną wartość siły naciągu liny konieczną do uniesienia leżącego słupa.
32.3.
Słup o długości 12 m był podnoszony bardzo powoli. Gdy był on już w położeniu prawie pionowym, lina odczepiła się od niego. W wyniku tej awarii słup się przewrócił.
Oblicz wartość prędkości liniowej końca słupa w chwili uderzenia o powierzchnię ziemi.
Przyjmij, że słup można potraktować jako cienki jednorodny pręt. Moment bezwładności takiego pręta względem osi prostopadłej do niego i przechodzącej przez jego koniec jest równy
, gdzie m jest masą pręta, a l – jego długością.
31.1.
1 – F,
2 – P,
3 – P.
32.2.
Moment
siły ciężkości działającej na słup musi się równoważyć z momentem
siły naciągu liny N. Oba momenty zapisujemy względem osi przechodzącej przez obrotową podstawę słupa.
Stąd po przekształceniu otrzymujemy
32.3.
Zadanie 33. (NR15)
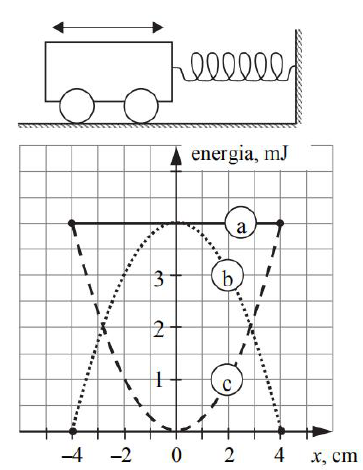
Wózek o masie 200 g jest doczepiony do sprężyny, której drugi koniec jest unieruchomiony (rysunek obok). Wózek wykonuje drgania wzdłuż osi poziomej. Opory ruchu, masę kółek i masę sprężyny pomijamy. Na wykresie poniżej przedstawiono w jednym układzie współrzędnych wykresy zależności energii kinetycznej, potencjalnej i całkowitej układu wózek – sprężyna od wychylenia wózka x.
33.1.
Wpisz do odpowiednich komórek poniższej tabeli obok każdej z nazw energii literę a, b lub c odpowiadającą wykresowi zależności tej energii od wychylenia x.
33.2.
Oceń prawdziwość poniższych zdań. Zaznacz P, jeśli zdanie jest prawdziwe, lub F – jeśli zdanie jest fałszywe.
- Energia kinetyczna wózka jest odwrotnie proporcjonalna do wychylenia x wózka z położenia równowagi. P F
- Energia potencjalna układu przy maksymalnym wychyleniu jest równa energii kinetycznej wózka przy przechodzeniu przez położenie równowagi. P F
- Energia całkowita układu jest zawsze równa maksymalnej energii kinetycznej wózka. P F
33.3.
Oblicz maksymalną prędkość, z jaką porusza się wózek.
33.4.
Oblicz okres drgań wózka.
33.1.
Wpisanie w kolejnych wierszach tabeli b, c i a.
33.2.
1 – F,
2 – P,
3 – P.
Odp.:
33.3.
Z wykresu odczytujemy maksymalną wartość energii kinetycznej wózka
. Tę wartość przyrównujemy do wyrażenia
i obliczamy
33.4.

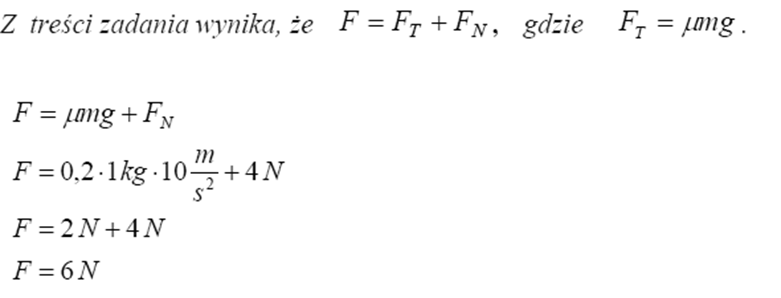
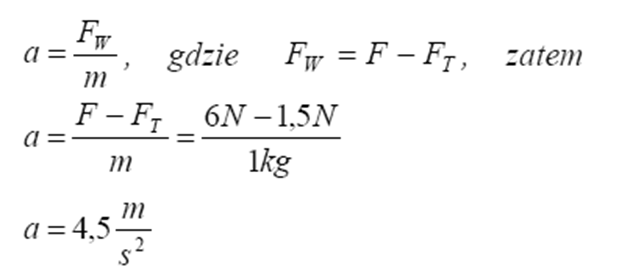
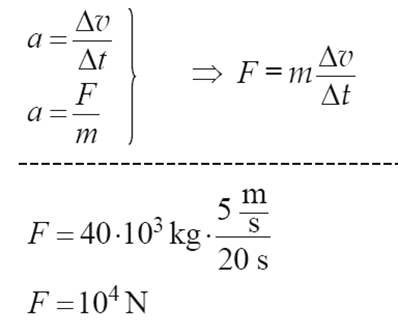
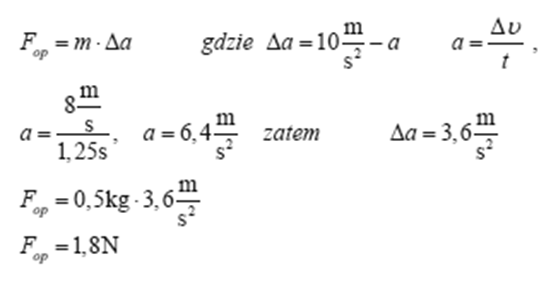

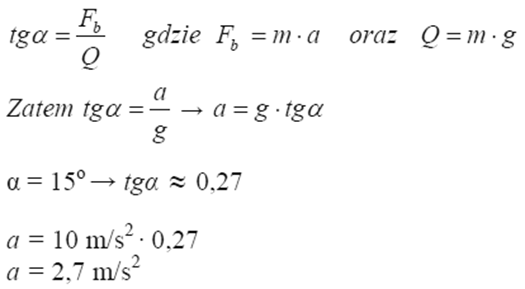

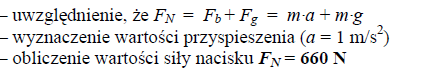


 11.2
11.2