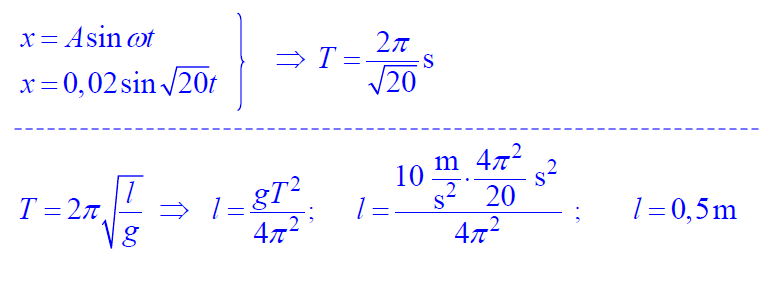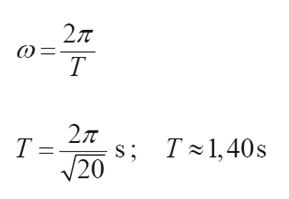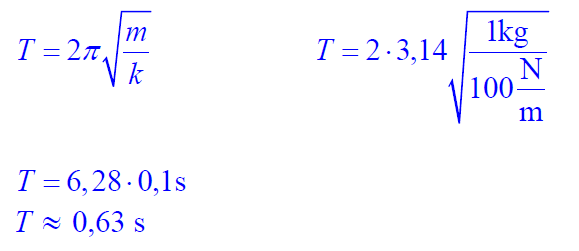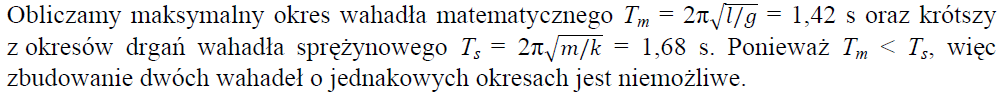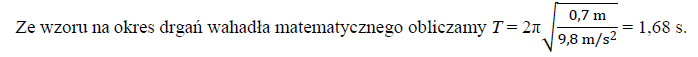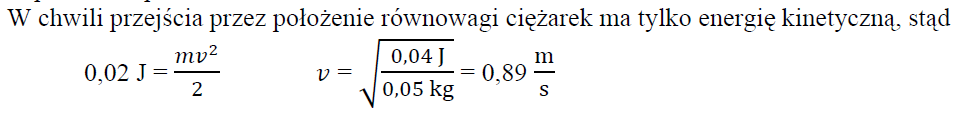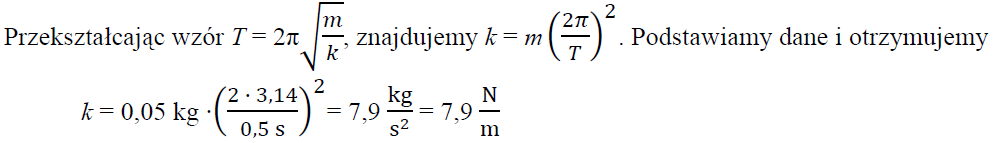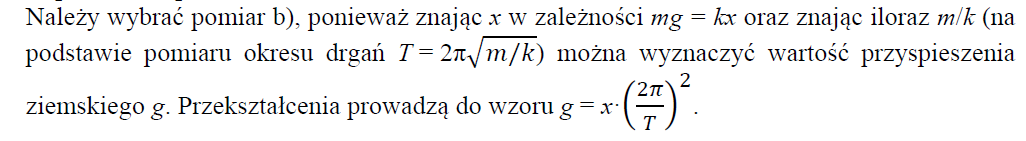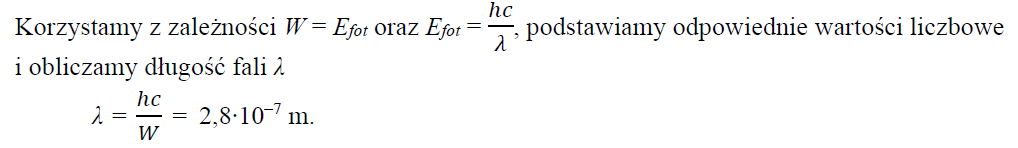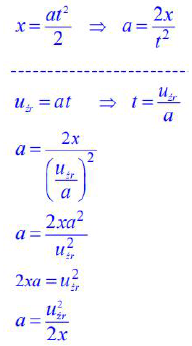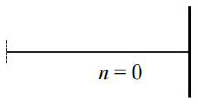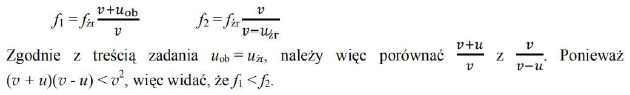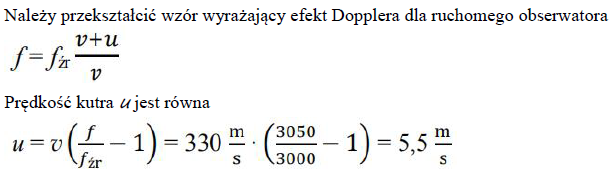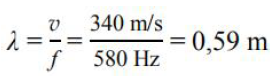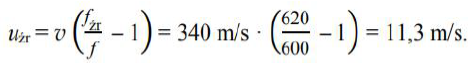Zadania maturalne z Fizyki
Temat: Drgania i fale
Zadania pochodzą z oficjalnych arkuszy maturalnych CKE, które służyły przeprowadzaniu majowych egzaminów. Czteroznakowy kod zapisany przy każdym zadaniu wskazuje na jego pochodzenie: S/N – „stara”/”nowa” formuła; P/R – poziom podstawowy/rozszerzony; np. 08 – rok 2008.
Zbiór zadań maturalnych w formie arkuszy, możesz pobrać >> TUTAJ <<.
Zadanie 1. (SP06)
Na nierozciągliwej cienkiej nici o długości 1,6 m zawieszono mały ciężarek, budując w ten
sposób model wahadła matematycznego.
1.1
Podaj, czy okres drgań takiego wahadła, wychylonego z położenia równowagi o niewielki kąt
ulegnie zmianie, jeśli na tej nici zawiesimy mały ciężarek o dwukrotnie większej masie Odpowiedź uzasadnij, odwołując się do odpowiednich zależności.
1.2
Oblicz liczbę pełnych drgań, które wykonuje takie wahadło w czasie 8 s, gdy wychylono je
o niewielki kąt z położenia równowagi i puszczono swobodnie. W obliczeniach przyjmij, że
wartość przyspieszenia ziemskiego jest równa 10 m/s2.
1.1
1.2
Zadanie 2. (SP06)
Jeżeli dwa jednakowe dźwięki docierają do ucha w odstępie czasu dłuższym niż 0,1 s są słyszane przez człowieka oddzielnie (powstaje echo). Jeśli odstęp czasu jest krótszy od 0,1 s dwa dźwięki odbieramy jako jeden o przedłużonym czasie trwania (powstaje pogłos). Oblicz, w jakiej najmniejszej odległości od słuchacza powinna znajdować się pionowa ściana odbijająca dźwięk, aby po klaśnięciu w dłonie słuchacz usłyszał echo. Przyjmij, że wartość prędkości dźwięku w powietrzu wynosi 340 m/s.
Zadanie 3. (SP07)
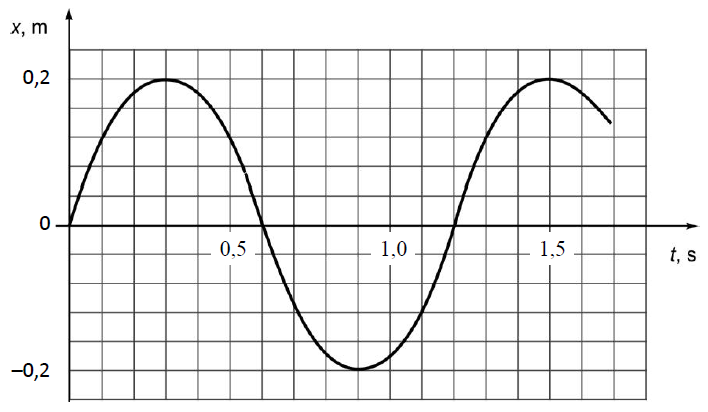
Równanie opisujące zależność wychylenia od czasu, dla małej kulki zawieszonej na cienkiej
nici i poruszającej się ruchem harmonicznym, ma w układzie SI postać: x = 0,02sin 20 t.
Do obliczeń przyjmij, że układ ten można traktować jako wahadło matematyczne oraz, że
wartość przyspieszenia ziemskiego jest równa 10 m/s2.
3.1.
Oblicz długość tego wahadła.
3.2
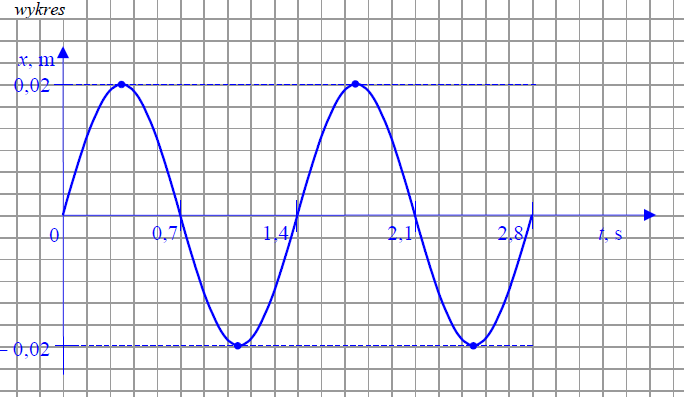
Przedstaw na wykresie zależność wychylenia tego wahadła od czasu. Na wykresie zaznacz
wartości liczbowe amplitudy oraz okresu drgań.
3.1.
3.2
Zadanie 4. (SP08)
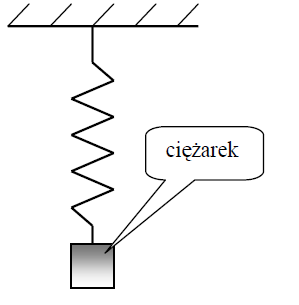
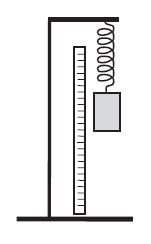
Metalowy ciężarek o masie 1 kg zawieszono na sprężynie jak na rysunku. Po zawieszeniu ciężarka sprężyna wydłużyła się o 0,1 m. Następnie ciężarek wprawiono w drgania w kierunku pionowym o amplitudzie 0,05 m. W obliczeniach przyjmij wartość przyspieszenia ziemskiego równą 10 m/s2, a masę sprężyny i siły oporu pomiń.
4.1
Wykaż, że wartość współczynnika sprężystości sprężyny wynosi 100 N/m.
4.2
Oblicz okres drgań ciężarka zawieszonego na sprężynie, przyjmując, że współczynnik
sprężystości sprężyny jest równy 100 N/m.
4.1
4.2
Zadanie 5. (SP09)
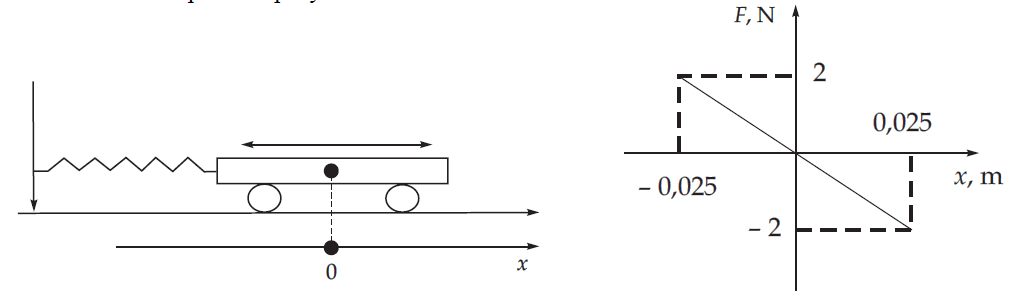
Wózek o masie 0,5 kg, połączony ze ścianą za pomocą sprężyny, wprawiono w drgania (rys.).
Na wykresie przedstawiono zależność siły powodującej ruch wózka od jego przemieszczenia.
W obliczeniach pomiń opory ruchu.
Zadanie 5.1
Oblicz współczynnik sprężystości sprężyny.
Zadanie 5.2
Wykaż, że maksymalna wartość przyspieszenia wózka wynosi 4 m/s2.
5.1
zapisanie zależności: i podstawienie wartości liczbowych odczytanych z wykresu
obliczenie współczynnika sprężystości sprężyny k = 80 N/m
5.2
zapisanie zależności i obliczenie maksymalnej wartości przyspieszenia amax = 4 m/s2
Zadanie 6. (SP11)
Ciało wykonuje prosty ruch harmoniczny. W momencie, w którym prędkość ciała jest
maksymalna, jego
- energia potencjalna jest maksymalna, a przyspieszenie równe zero.
- energia potencjalna jest minimalna, a przyspieszenie równe zero.
- energia potencjalna jest minimalna, a przyspieszenie jest maksymalne.
- energia potencjalna i przyspieszenie przyjmują wartości maksymalne.
Zadanie 7. (SP11)
Dwie koleżanki chciały wyznaczyć masę arbuza. Nie miały wagi kuchennej, ale wykorzystały
sprężynę, linijkę i paczkę cukru o masie 1 kg. Zawieszenie paczki cukru na sprężynie spowodowało wydłużenie sprężyny o 4 cm. Zawieszenie arbuza wydłużyło ją o 9 cm.
7..1
Wyznacz wartość stałej sprężystości sprężyny.
7.2
Wyznacz masę arbuza.
7..1
Przyrównujemy siłę ciężkości mg do siły sprężystości kx i przekształcamy do postaci
k = mg/x. Podstawiamy dane (poprawna jest zarówno wartość g = 10 m/s2, jak g = 9,81 m/s2) i obliczamy k. Poprawny wynik: k = 2,5 N/cm, lub 2,45 N/cm, lub 250 N/m, lub 245 N/m.
7.2
Masa arbuza wynosi 2,25 kg (od 2,2 kg do 2,3 kg), wynik otrzymany na podstawie wzoru
mg = kx lub proporcji m1/m2 = x1/x2.
Zadanie 8. (SP12)
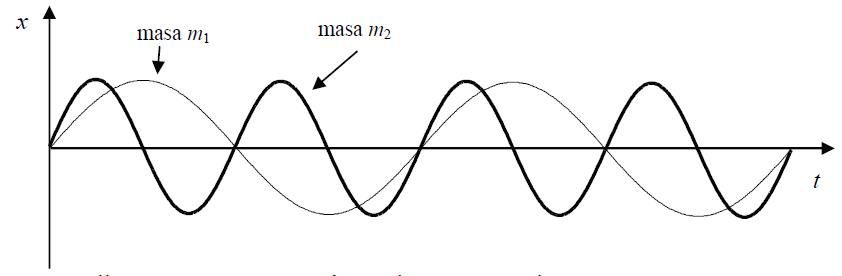
Wykres przedstawia zależność wychylenia od czasu dla dwóch mas m1 lub m2 zawieszonych kolejno na tej samej sprężynie.
Z wykresu wynika, że masa m2 w porównaniu z masą m1 jest
- 4 razy większa.
- 2 razy większa.
- 2 razy mniejsza.
- 4 razy mniejsza.
Zadanie 9. (SP12)
Uczeń chce zbudować dwa wahadła: matematyczne i sprężynowe, o takim samym okresie drgań. Dysponuje lekką sprężyną o współczynniku sprężystości równym 7 N/m, dwoma małymi ciężarkami o masie 500 g każdy oraz nicią o długości 0,5 m (którą można skrócić w razie potrzeby).
9.1
Wykaż, wykonując obliczenia, że uczniowi nie uda się zrealizować tego pomysłu.
9.2
Oprócz przedmiotów wymienionych wyżej uczeń otrzymał trzeci ciężarek o masie 500 g, który można zawiesić razem z jednym z dwóch poprzednich. Czy teraz zbudowanie zaplanowanych wahadeł jest możliwe? Napisz i uzasadnij odpowiedź.
9.1
9.2
Dodatkowy ciężarek nie zmieni okresu wahadła matematycznego, a wydłuży okres wahadła sprężynowego, zatem zbudowanie wahadeł o równych okresach drgań będzie nadal niemożliwe.
Zadanie 10. (SP13)
W pociągu zawieszono małe ciężarki na niciach o różnych długościach. Koła pociągu,
przejeżdżając przez złączenia szyn, powodowały wstrząsy wagonu i wychylenia ciężarków
z położenia równowagi. Jeden z ciężarków wychylał się z amplitudą znacznie większą
od pozostałych.
10.1
Podaj nazwę zjawiska, które spowodowało większą wartość amplitudy wahań tego ciężarka.
10.2
Wykaż, wykonując obliczenia, że okres wahań ciężarka zawieszonego na nici o długości
70 cm wynosi 1,68 s.
10.3
Długość szyn na tym odcinku toru wynosi 25 m. Przyjmijmy, że podczas przejazdu wagonu
przez złączenie szyn następował jeden wstrząs wpływający na wychylenie ciężarka, a kolejne
wstrząsy następowały w odstępach czasu równych okresowi wahań ciężarka zawieszonego na
nici o długości 70 cm. Wiedząc, że okres wahań tego ciężarka wynosi 1,68 s, oblicz prędkość
pociągu. Wynik podaj w km/h.
10.1
Zjawiskiem tym jest rezonans.
10.2
10.3
Z podzielenia drogi 25 m przez czas 1,68 s, po przeliczeniu jednostek, obliczamy prędkość równą 53,6 km/h.
Zadanie 11. (SP14)
Dwoje uczniów ogląda film, w którym załoga statku kosmicznego podczas bitwy w przestrzeni międzyplanetarnej widzi wybuch innego statku i po chwili słyszy odgłos wybuchu. Uczniowie uważają, że nie jest to realne. Uczniowie
- mają rację, ponieważ fale dźwiękowe nie przenikają przez kadłub statku kosmicznego.
- mają rację, ponieważ fale dźwiękowe nie rozchodzą się w próżni.
- mają rację, ponieważ w próżni dźwięk biegnie z prędkością równą prędkości światła.
- nie mają racji, ponieważ odgłos wybuchu byłby rzeczywiście słyszalny.
Zadanie 12. (SP14)
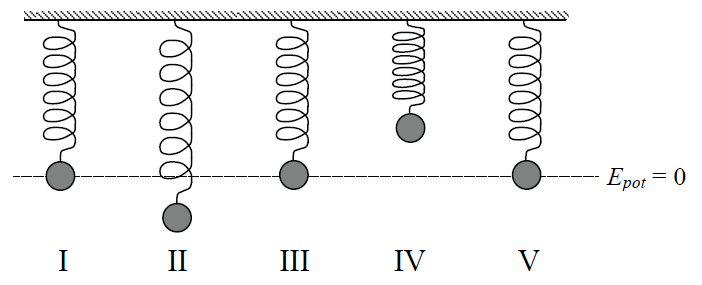
Ciężarek o masie 0,05 kg zawieszono na sprężynie i wzbudzono drgania harmoniczne.
Na rysunku pokazano kolejne położenia ciężarka w odstępach czasu co 0,5 s. W chwili I
ciężarek znajdował się w położeniu równowagi, a w chwili II miało miejsce maksymalne
wychylenie.
12.1
Napisz wartość okresu drgań tego ciężarka.
12.2
Całkowita energia mechaniczna tego ciężarka wynosi 0,02 J. Oblicz wartość prędkości ciężarka przy przejściu przez położenie równowagi.
12.3
Ciężarek zawieszono na innej sprężynie, dla której okres drgań ciężarka był równy 0,5 s.
Oblicz współczynnik sprężystości tej sprężyny.
12.1
Okres drgań ciężarka wynosi 2 s.
12.2
12.3
Zadanie 13. (NP15)
Uczeń przeprowadził doświadczenie polegające na pomiarze okresu drgań pewnego wahadła.
Pomiary wykonywał dwoma sposobami:
a) mierzył czas trwania jednego okresu,
b) mierzył łączny czas trwania 10 kolejnych okresów i wynik pomiaru dzielił przez 10.
Napisz, który sposób pozwalał uzyskać dokładniejszą wartość okresu drgań tego wahadła.
Swój wybór krótko uzasadnij.
Dokładniejszą wartość okresu drgań można otrzymać sposobem b), gdyż wtedy zmniejszona jest niepewność związana z reakcją ucznia na ruch wahadła.
Zadanie 14. (NP15)
Na wykresie przedstawiono zależność wychylenia od czasu dla ciężarka zawieszonego na
sprężynie. Współczynnik sprężystości sprężyny jest równy 10 N/m.
14.1
Oblicz częstotliwość drgań ciężarka oraz jego masę.
14.2
Oszacuj wartość prędkości ciężarka w chwili, gdy przechodzi on przez położenie równowagi.
Możesz skorzystać z definicji prędkości chwilowej.
14.1
14.2
Zadanie 15. (NP16)
Jeżeli długość wahadła matematycznego wzrośnie cztery razy, to częstotliwość drgań harmonicznych tego wahadła
- zmaleje dwukrotnie.
- zmaleje czterokrotnie.
- wzrośnie dwukrotnie.
- wzrośnie czterokrotnie.
Zadanie 16. (NP16)
Sprężyna rozciąga się o 1 cm, gdy działamy na nią siłą o wartości 1 N. Tę sprężynę przyczepiono do klocka o masie 1 kg poczywającego na poziomej powierzchni i działano na jej koniec siłami o różnej wartości, próbując wprawić klocek w ruch.
16.1
Prawy koniec sprężyny pociągnięto, wskutek czego rozciągnęła się ona o 5 cm, ale klocek
nadal pozostawał w spoczynku. Nazwij wszystkie siły działające na klocek w kierunku
poziomym i oblicz ich wartości.
16.2
Oblicz maksymalne wydłużenie sprężyny, przy którym klocek pozostaje w spoczynku, jeśli współczynnik tarcia statycznego klocka o podłoże wynosi 0,65.
16.3
Po wprawieniu klocka w ruch możemy go przesuwać ze stałą prędkością, działając poziomą siłą o wartości 5 N. Oblicz współczynnik tarcia kinetycznego.
16.1
Na klocek działają siły sprężystości i tarcia (lub tarcia statycznego), każda o wartości 5 N.
16.2
Ze wzoru T = μmg obliczamy maksymalną siłę tarcia T = 6,4 N. Tyle samo wynosi siła
sprężystości, zatem wydłużenie sprężyny wynosi 6,4 cm.
16.3
Do wzoru FT = μFN podstawiamy FT = 5 N i FN = mg = 9,8 N. Obliczamy μ = 0,51.
Zadanie 17. (NP16)
Jeżeli ma się do dyspozycji sprężynkę, ciężarek, linijkę, statyw i stoper, to można wyznaczyć przyspieszenie ziemskie bez najomości zarówno masy ciężarka, jak i stałej sprężystości sprężynki. W tym celu należy w pierwszym pomiarze zawiesić ciężarek na sprężynce zob. rysunek), wprowadzić go w drgania pionowe i zmierzyć okres drgań. W drugim pomiarze należy wykorzystać linijkę do jednego z dwóch celów:
a) pomiar amplitudy drgań ciężarka,
b) pomiar długości sprężynki wiszącej bez ciężarka, zawieszenie na niej ciężarka bez wzbudzania drgań i pomiar wydłużenia sprężynki.
17.1
Napisz, który z wymienionych pomiarów a) i b) należy wybrać, aby na jego podstawie oraz na podstawie pomiaru okresu drgań wyznaczyć przyspieszenie ziemskie. Uzasadnij dokonany wybór. Wyprowadź wzór, z którego można obliczyć przyspieszenie ziemskie, korzystając z wyników tych pomiarów.
17.2
Podaj dwie możliwe przyczyny niepewności wartości przyspieszenia ziemskiego obliczonego na podstawie opisanych pomiarów. Dla każdej z nich podaj metodę zmniejszenia jej wpływu na niepewność wyniku.
Przyczyna 1: ……………………………………….
Zmniejszenie niepewności można osiągnąć następującą metodą:
Przyczyna 2: ……………………………………….
Zmniejszenie niepewności można osiągnąć następującą metodą:
17.1
17.2
Przyczynami niepewności wartości przyspieszenia ziemskiego mogą być np.: niedokładność odczytu wydłużenia sprężyny wg linijki i niedokładność pomiaru czasu stoperem. Zmniejszenie niepewności można osiągnąć np. metodą kilkakrotnego powtórzenia pomiarów i obliczenia średniej lub mierząc czas 10 drgań i dzieląc wynik pomiaru przez 10.
Zadanie 18. (NP17)
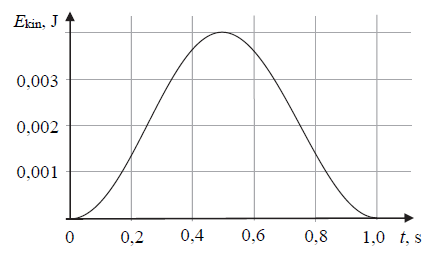
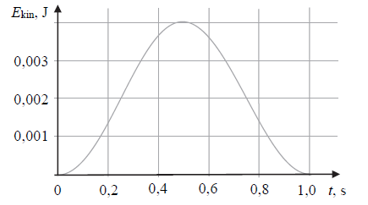
Wahadło, które jest dobrym przybliżeniem wahadła matematycznego, zbudowano z ciężarka o masie 0,1 kg zawieszonego na długiej, cienkiej i nierozciągliwej nici. Na wykresie przedstawiono zależność energii kinetycznej wahadła od czasu.
18.1
Ustal, korzystając z informacji na wykresie, okres drgań wahadła i oblicz jego długość.
18.2
Ustal i zapisz, w których chwilach t w przedziale czasu widocznym na wykresie wychylenie wahadła jest równe połowie amplitudy drgań. Skorzystaj z podanego w zadaniu wykresu zależności energii kinetycznej wahadła od czasu.
18.3
Drgania wahadła odbywają się w powietrzu i dlatego niektóre wielkości opisujące drgania wahadła mogą się zmieniać. Zakładamy przy tym, że opory powietrza tłumiące te drgania są na tyle małe, że okres takich drgań można uznać za równy okresowi wahadła matematycznego (w rzeczywistości jest nieco większy).
18.1
a) W obwodzie wystąpił przepływ prądu, gdyż światło padające na płytkę wybiło z niej elektrony (lub wystąpiło jawisko fotoelektryczne).
b) Oświetlono płytkę P, ponieważ jest ona dołączona do ujemnego bieguna źródła napięcia, czyli wybite elektrony będą przepływać do drugiej płytki.
18.2
18.3
Zadanie 19. (NP18)
W powietrzu, przy tych samych warunkach atmosferycznych, rozchodzą się dwie fale
dźwiękowe. Pierwsza z nich ma częstotliwość f, a druga – częstotliwość 2f. Z tego wynika, że
druga fala ma
- dwukrotnie większą prędkość niż fala pierwsza.
- dwukrotnie mniejszą prędkość niż fala pierwsza.
- dwukrotnie większą długość niż fala pierwsza.
- dwukrotnie mniejszą długość niż fala pierwsza.
Zadanie 20. (NP19)
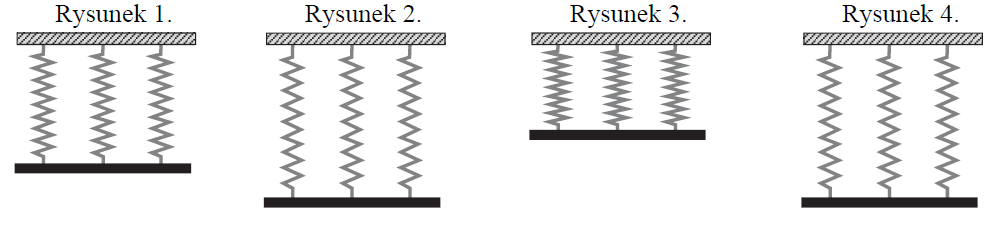
Pręt zawieszono poziomo na trzech identycznych, bardzo lekkich sprężynach, których górne końce przymocowano do sufitu (zobacz rysunek 1.). Następnie ten pręt wychylono w kierunku pionowym z położenia równowagi sił, po czym puszczono. Skutkiem tego pręt wraz z układem sprężyn został wprawiony w drgania o kierunku pionowym tak, że położenie chwilowe pręta zawsze było poziome (zobacz rysunki 2.–4.). Okres drgań opisanego układu był równy T1.
Zadanie 21. (SR06)
Laser o mocy 0,1 W emituje w próżni monochromatyczną wiązkę światła o długości fali 633 nm i kołowym przekroju.
Oblicz najwyższy rząd widma, jaki można zaobserwować po skierowaniu tej wiązki prostopadle na siatkę dyfrakcyjną posiadającą 400 rys/mm.
Zadanie 22. (SR07)
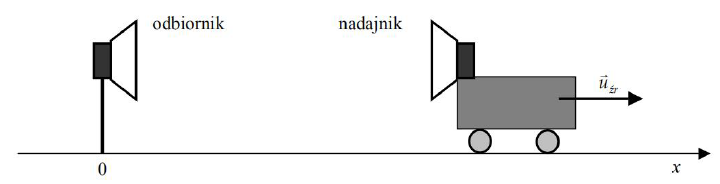
Wózek z nadajnikiem fal ultradźwiękowych, spoczywający w chwili t = 0, zaczyna oddalać się od nieruchomego odbiornika ruchem jednostajnie przyspieszonym.
22.1
Napisz, jakim ruchem i w którą stronę powinien poruszać się nieinercjalny układ odniesienia, aby opisywany w tym układzie wózek pozostawał w spoczynku.
22.2
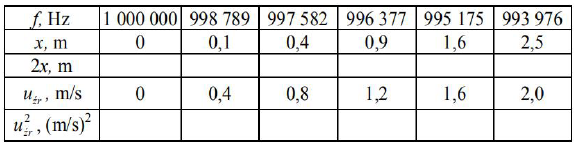
W tabeli przedstawiono wyniki pomiarów częstotliwości odbieranej przez odbiornik, położenia oraz wartości prędkości dla poruszającego się wózka, dokonanych za pomocą automatycznego układu Przyjmij, że wartość prędkości ultradźwięków w powietrzu wynosi 330 m/s.
Uzupełnij tabelę, wykonując niezbędne obliczenia.
22.3
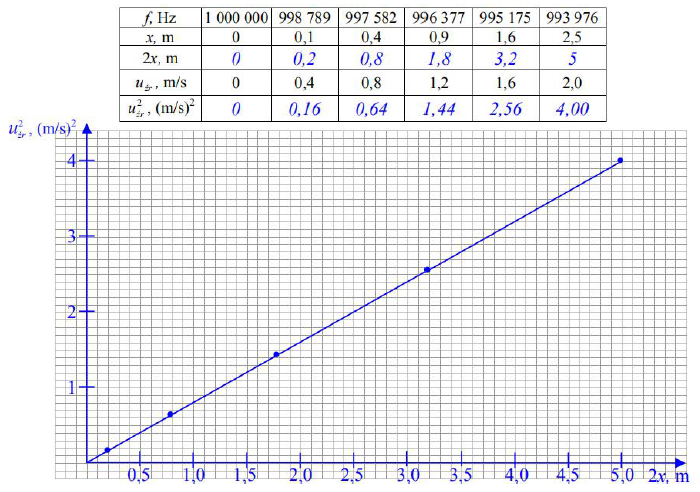
Narysuj wykres zależności uź2r od 2x obliczając i uzupełniając brakujące wartości w tabeli.
22.4
Wyprowadź zależność matematyczną pozwalają cą obliczyć wartość przyspieszenia wózka.
Przyjmij, że dane są tylko położenie x i prędkość uźr wózka.
22.5
Oblicz wartość przyspieszenia wózka.
22.1
Nieinercjalny układ odniesienia powinien poruszać się ruchem jednostajnie przyspieszonym. Układ odniesienia powinien poruszać się w prawo.
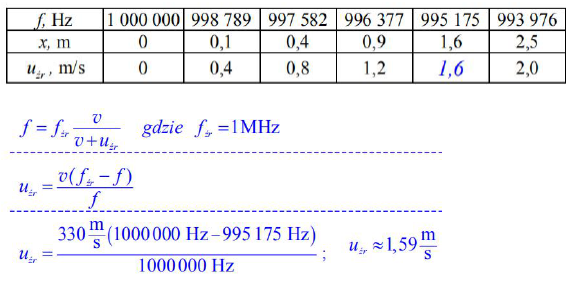
22.2
22.3
22.4
22.5
Zadanie 23. (SR12)
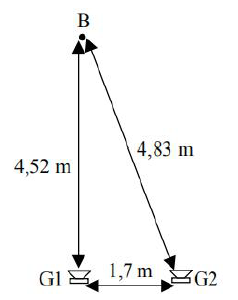
Dwa głośniki G1 i G2 są podłączone do tego samego generatora sygnału harmonicznego (sinusoidalnego) o częstotliwości 2200 Hz. Głośniki ustawiono w odległości 1,7 m od siebie, a mikrofon w punkcie B – jak na rysunku. Zestaw znajduje się w powietrzu, w którym prędkość dźwięku wynosi 340 m/s. Głośniki i mikrofon są bardzo małe.
Zadanie 23.1
Wykaż, wykonując obliczenia, że efektem nałożenia na siebie fal dźwiękowych w B jest ich wzmocnienie.
Zadanie 23.2
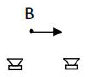
W punkcie B natężenie dźwięku jest duże. W którym kierunku należy przesunąć mikrofon, aby na jak najkrótszej drodze przejść do punktu, gdzie natężenie dźwięku jest małe? Narysuj strzałkę od B we właściwym kierunku.
Informacja do zadań 23.3–23.5
Przesunięto mikrofon i okazało się, że w nowym położeniu C natężenie dźwięku jest znacznie mniejsze niż w B.
Zadanie 23.3
Zmieniono biegunowość przyłączenia głośnika G2 do generatora. Po tej zmianie, gdy membrana G1 porusza się w przód, membrana G2 cofa się i odwrotnie. Opisz zmianę natężenia dźwięku w punktach B i C i podaj jej przyczynę.
Zadanie 23.4
Wybierz poprawne zakończenie poniższego zdania, podkreślając właściwe wyrażenie.
Gdy zwiększono częstotliwość sygnału generatora, odległość od punktu, w którym dźwięk jest wzmocniony, do najbliższego punktu, w którym jest osłabiony
wzrosła zmalała nie zmieniła się.
Uzasadnij swój wybór.
Zadanie 23.5
Wybierz poprawne zakończenie poniższego zdania, podkreślając właściwe wyrażenie.
Gdy zwiększono odległość między głośnikami G1 i G2, odległość od punktu, w którym dźwięk jest wzmocniony, do najbliższego punktu, w którym jest osłabiony
wzrosła zmalała nie zmieniła się.
23.1
Różnica odległości głośników od punktu B wynosi s = 0,31 m, a długość fali dźwiękowej jest równa λ = 0,155 m. Ponieważ s jest całkowitą wielokrotnością λ, to fazy obu fal są zgodne, czyli następuje wzmocnienie.
23.2
23.3
Po odwróceniu biegunowości zasilania głośnika G2 nastąpi osłabienie dźwięku (interferencja destruktywna) w punkcie B i wzmocnienie (interferencja konstruktywna) w punkcie C, ponieważ odwrócenie biegunowości spowodowało odwrócenie fazy jednej z fal.
23.4
Odległość od punktu, w którym dźwięk jest wzmocniony, do najbliższego punktu, w którym jest osłabiony zmalała. Wynika to stąd, że wzrost częstotliwości powoduje skrócenie długości fali.
23.5
Odległość od punktu, w którym dźwięk jest wzmocniony, do najbliższego punktu, w którym jest osłabiony zmalała.
Zadanie 24. (SR14)
Zadanie 24.1
Uczniowie mają do dyspozycji: źródło światła białego (żarówkę), siatkę dyfrakcyjną o znanej odległości między szczelinami (rysami), ekran, linijkę oraz przesłonę z wąską szczeliną. Ich zadaniem jest wyznaczenie zakresu długości fal światła widzialnego, z wykorzystaniem widma rzędu n = 1.
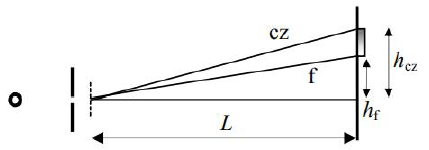
Na poniższym rysunku dorysuj przesłonę we właściwym położeniu (pozwalającym obserwować widmo na ekranie) oraz bieg promieni czerwonego i fioletowego. Zaznacz wielkości potrzebne do wyznaczenia zakresu długości fal światła widzialnego.
Napisz wzory pozwalające obliczyć największą i najmniejszą długość fali światła białego z wykorzystaniem wprowadzonych wielkości. Możesz przyjąć, że kąty są małe (tg α = sin α).
Zadanie 24.2
Na rysunku do zadania 24.1 zaznacz padający na ekran promień rzędu zerowego i oznacz ten promień „n = 0”. Napisz, dlaczego w rzędzie n = 0 obserwujemy na ekranie plamę białego światła, a nie – kolorowy pasek (jak w innych rzędach).
Zadanie 24.3
Dla światła możemy obserwować zjawisko polaryzacji. Napisz, dlaczego nie obserwuje się polaryzacji fal dźwiękowych rozchodzących się w powietrzu.
24.1
Odległości hcz i hf na ekranie są powiązane z kątami ugięcia promieni αcz i αf wzorami hcz = L tg αcz, hf = L tg αf.
Podstawiamy tg α = sin α i n = 0 do równania nλ = d sin α (d – odległość między rysami siatki) i otrzymujemy
24.2
W rzędzie n = 0 nie ma różnicy dróg optycznych. Kąt ugięcia promienia jest równy 0 dla wszystkich długości fali.
24.3
Nie obserwuje się polaryzacji fal dźwiękowych w powietrzu, ponieważ dźwięk w powietrzu jest falą podłużną, a polaryzacja może zachodzić tylko dla fal poprzecznych.
Zadanie 25. (SR14)
W poniższych zadaniach przyjmujemy, że nie ma wiatru (powietrze jest nieruchome względem ziemi), a rozpatrywane ruchy zachodzą wzdłuż prostej, na której leżą zarówno źródło, jak i odbiornik dźwięku.
Zadanie 25.1
Podkreśl poprawne uzupełnienia zdań 1 i 2.
- Jeżeli źródło dźwięku o stałej częstotliwości oddala się ruchem jednostajnym od nieruchomego odbiornika, to częstotliwość odbierana przez odbiornik jest (stała / rosnąca /malejąca) i (większa od / mniejsza od / równa) częstotliwości dźwięku emitowanego przez źródło.
- Częstotliwość dźwięku syreny karetki docierającego do ucha przechodnia jest (większa / mniejsza) wtedy, gdy przechodzień biegnie do stojącej karetki, niż wtedy, gdy karetka zbliża się z prędkością o tej samej wartości do stojącego przechodnia.
Powołując się na odpowiednie wzory, uzasadnij wybór dokonany w zdaniu 2.
Zadanie 25.2
Podczas mgły buczek (syrena) nieruchomego statku wysyła sygnały dźwiękowe o częstotliwości 3000 Hz. Rybak znajdujący się na kutrze płynącym w stronę statku odbiera sygnał o częstotliwości 3050 Hz. Oblicz wartość prędkości, z jaką porusza się kuter. Prędkość dźwięku w powietrzu wynosi 330 m/s.
Zadanie 25.3
Natężenie dźwięku to średnia moc fali przypadająca na jednostkę pola powierzchni.
Syrena alarmowa emituje dźwięk o mocy 10 W. Oblicz natężenie dźwięku w odległości 5 km od syreny, zakładając, że dźwięk ten rozchodzi się jednakowo we wszystkich kierunkach. Czy dźwięk ten będzie słyszalny w tej odległości, jeśli niezbędny do tego poziom natężenia wynosi 30 dB? Napisz odpowiedź i ją uzasadnij.
Dane są wzory na pole powierzchni kuli S = 4πr
objętość kuli V =
πr
.
25.1
Podkreślenia w zdaniu 1: stała, mniejsza od. Podkreślenie w zdaniu 2: mniejsza.
Oznaczmy częstotliwość słyszaną przez przechodnia biegnącego do stojącej karetki przez f1, a częstotliwość słyszaną przez nieruchomego przechodnia, do którego zbliża się karetka, przez f2. Efekt Dopplera dla tych przypadków jest opisany wzorami
25.2
25.3
Zadanie 26. (SR15)
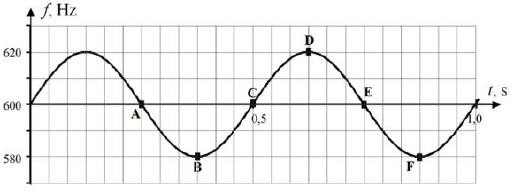
Głośnik podłączony przewodami do generatora napięcia przemiennego o częstotliwości 600 Hz wprawiono w ruch jednostajny po okręgu w płaszczyźnie poziomej. W dużej odległości od głośnika nieruchomy obserwator (znajdujący się na tej samej wysokości co głośnik) zarejestrował fale dźwiękowe o zmieniającej się częstotliwości. Zależność częstotliwości odbieranych fal od czasu przedstawiono na wykresie poniżej. W obliczeniach przyjmij, że prędkość rozchodzenia się fali dźwiękowej w powietrzu równa jest 340 m/s.
Zadanie 26.1.
Oblicz największą długość fali odbieranej przez obserwatora.
Zadanie 26.2.
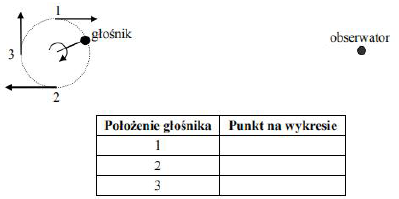
Na rysunku zaznaczono położenie obserwatora oraz wektory prędkości głośnika dla jego trzech różnych położeń. Wpisz do tabeli, które punkty na wykresie (A, B, C, D, E, F) odpowiadają poszczególnym położeniom głośnika.
Zadanie 26.3.
Korzystając z informacji zawartych na wykresie, wykaż, że wartość prędkości głośnika wynosiła około 11 m/s.
Zadanie 26.4.
Wartość prędkości głośnika wynosiła 11 m/s. Oblicz promień okręgu, po jakim się on poruszał.
Zadanie 26.5.
Głośnik wysyła dźwięk jednakowo we wszystkich kierunkach, a jego moc akustyczna wynosi 2 W. Oblicz, w jakiej odległości powinien znajdować się obserwator, żeby poziom natężenia odbieranego przez niego dźwięku wynosił 70 dB.
26.1
Największa długość fali odpowiada najniższej częstotliwości, czyli 580 Hz. Obliczamy
26.2
Do tabeli wpisujemy w położeniu 1 – D, w położeniu 2 – B lub F, a w położeniu 3 – C, A lub E.
26.3
Z wykresu odczytujemy maksymalną częstotliwość 620 Hz, odpowiadającą najszybszemu zbliżaniu głośnika do obserwatora, albo też minimalną 580 Hz, odpowiadającą najszybszemu oddalaniu. Do analizy zjawiska Dopplera wykorzystujemy wzór gdzie
minus w mianowniku odpowiada maksymalnej częstotliwości, a plus – minimalnej. Jeśli wybierzemy minus i maksymalną częstotliwość, to
26.4
Z wykresu odczytujemy okres ruchu T = 0,5 s i obliczamy promień okręgu
26.5
Zadanie 27. (NR15)
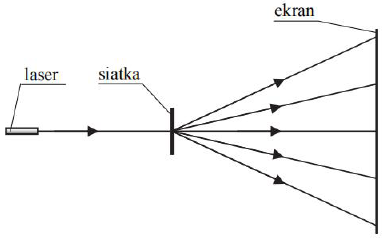
Laser, siatkę dyfrakcyjną oraz ekran umieszczono w ustalonych wzajemnych odległościach (rysunek obok). Po włączeniu lasera na ekranie zaobserwowano świecące punkty.
Zaznacz właściwe uzupełnienie poniższego zdania wybrane spośród A–C oraz uzasadnienie wybrane spośród 1–3.
Po całkowitym zanurzeniu siatki oraz ekranu w wodzie i oświetleniu siatki światłem tego samego lasera odległość pomiędzy kolejnymi punktami na ekranie
C – 3