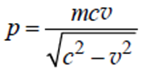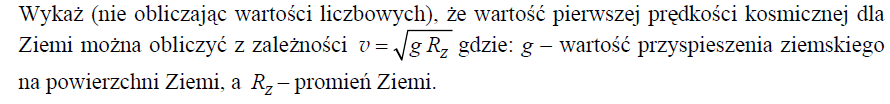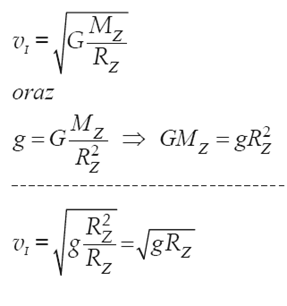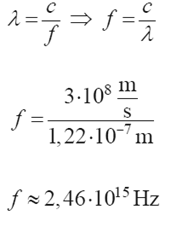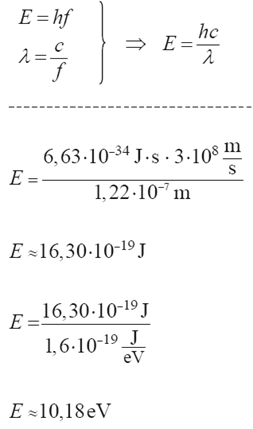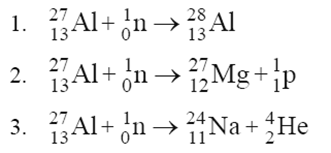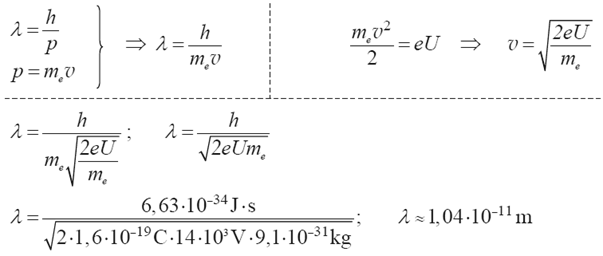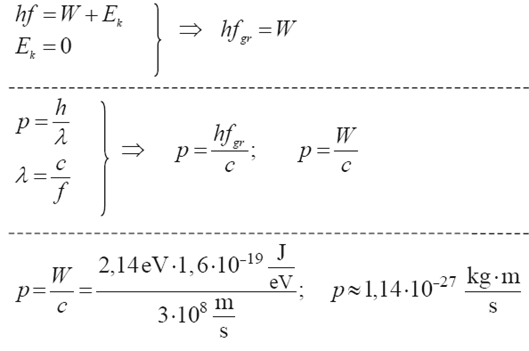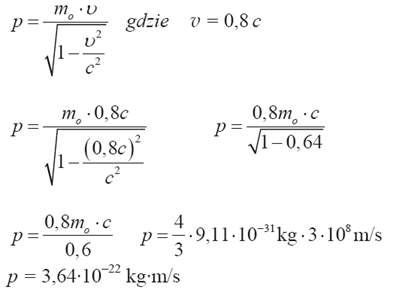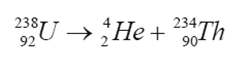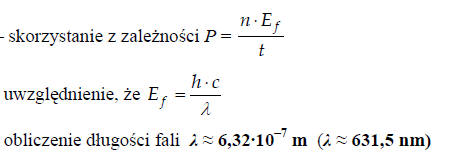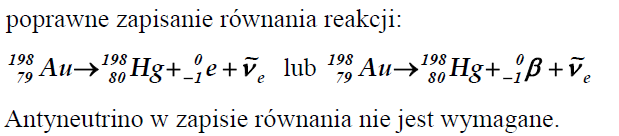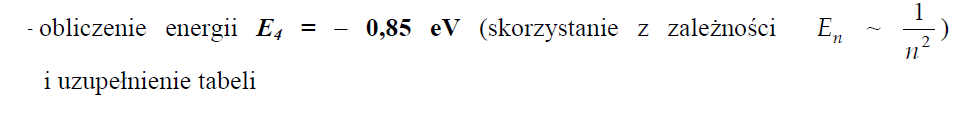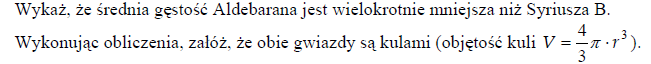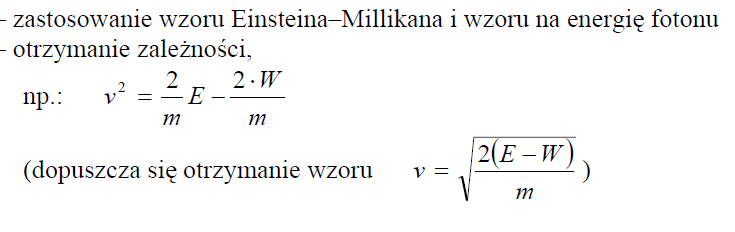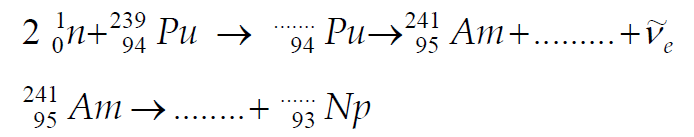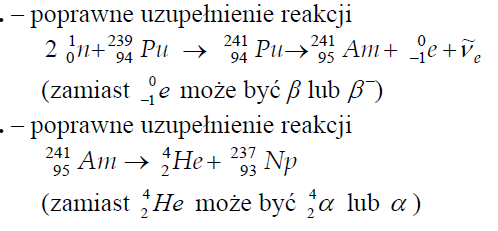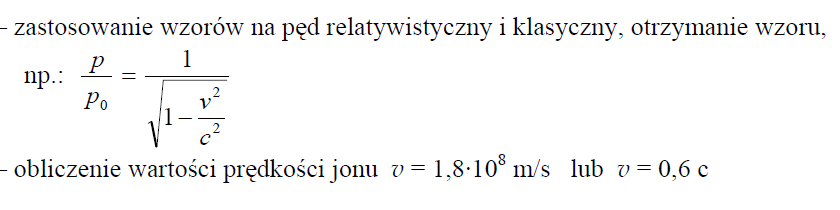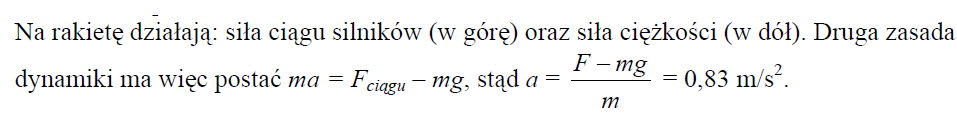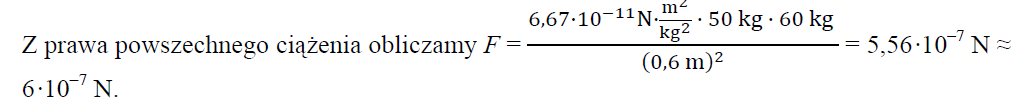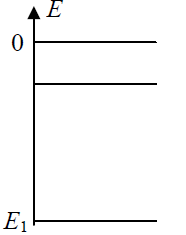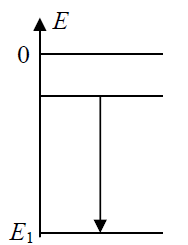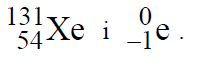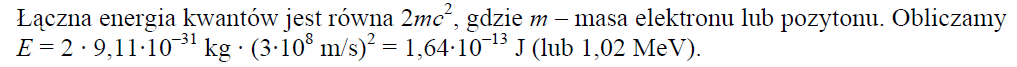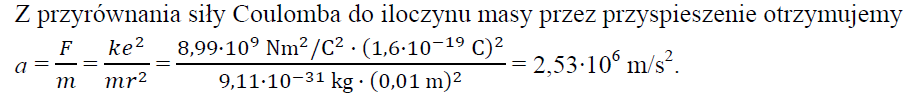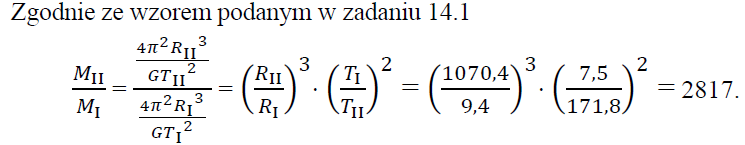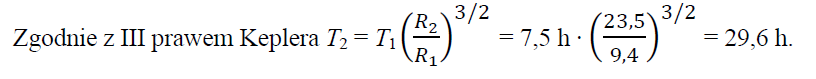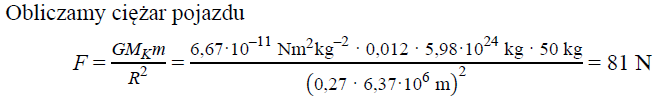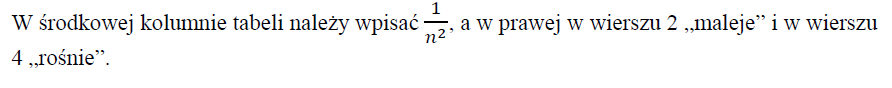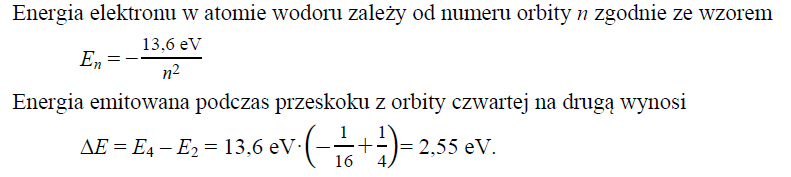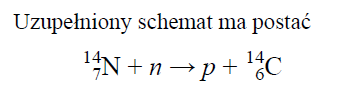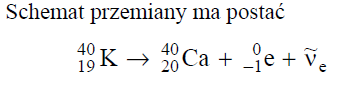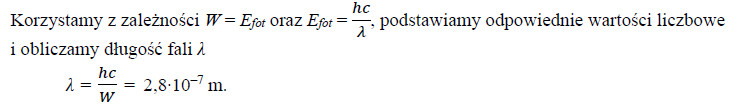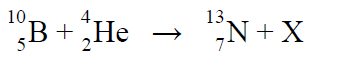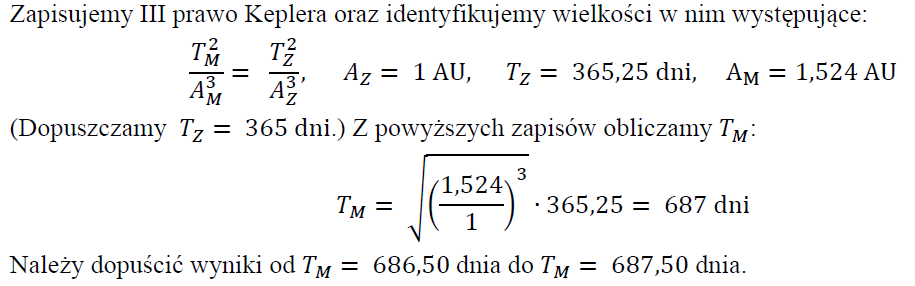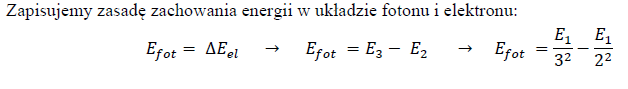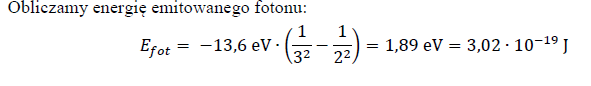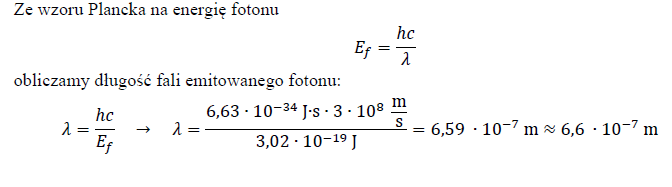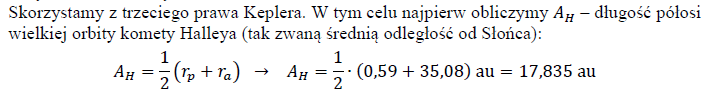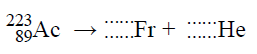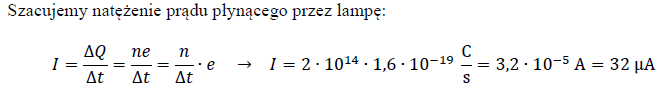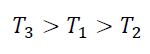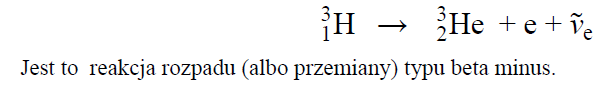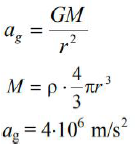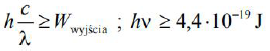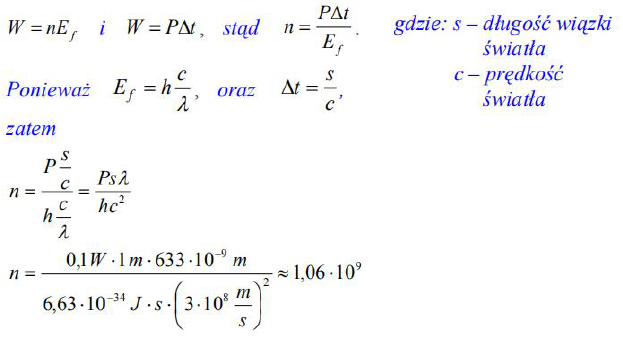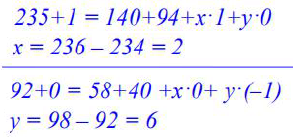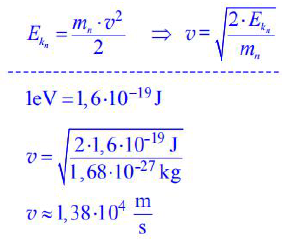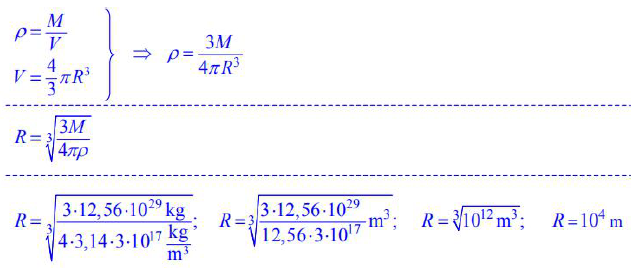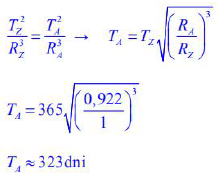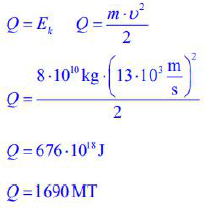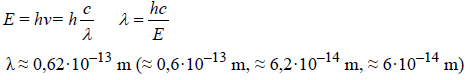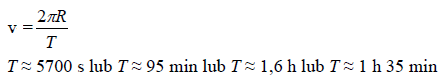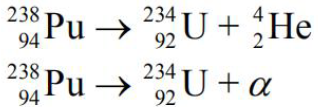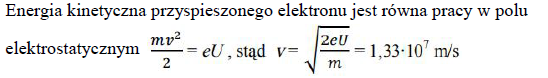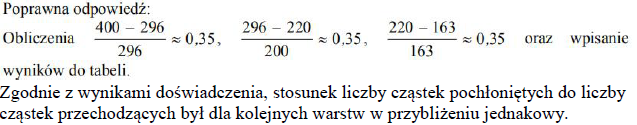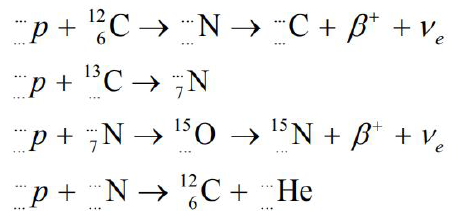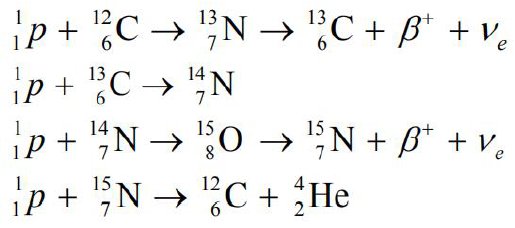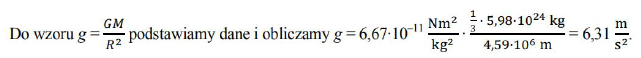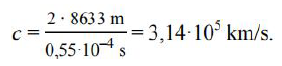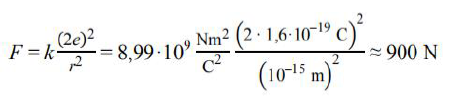Zadania maturalne z Fizyki

Temat: Fizyka kwantowa i astronomia

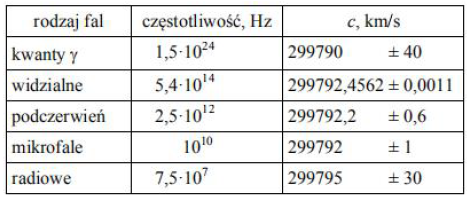
Zadania pochodzą z oficjalnych arkuszy maturalnych CKE, które służyły przeprowadzaniu majowych egzaminów. Czteroznakowy kod zapisany przy każdym zadaniu wskazuje na jego pochodzenie: S/N – „stara”/”nowa” formuła; P/R – poziom podstawowy/rozszerzony; np. 08 – rok 2008.

Zbiór zadań maturalnych w formie arkuszy, możesz pobrać >> TUTAJ <<.

Zadanie 1. (SP05)

Nasza Galaktyka

1. jest galaktyką spiralną i kształtem przypomina spłaszczony dysk.
2. jest nazywana Drogą Mleczną, a Słońce znajduje się w jej środku.
3. jest największą galaktyką kołową w Układzie Lokalnym.
4. jest jedyną galaktyką na naszym niebie, widoczną jako pojedynczy obiekt.

Zadanie 2. (SP05)

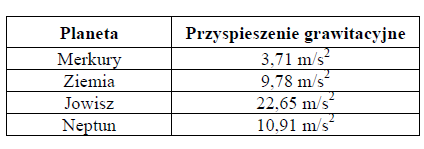
W tabeli zamieszczono przyspieszenia grawitacyjne na powierzchni wybranych planet Układu Słonecznego.

Długość wahadła matematycznego o okresie drgań równym 1 s, będzie największa na

1. Merkurym.
2. Ziemi.
3. Jowiszu.
4. Neptunie.

Zadanie 3. (SP05)
Wartość pędu cząstki o masie spoczynkowej m poruszającej się z prędkością o wartości v, porównywalnej z prędkością światła c, wyraża się wzorem:

Na tej podstawie możemy stwierdzić, że:

1. wartość pędu cząstki nie zależy od wartości prędkości.
2. wartość pędu cząstki jest wprost proporcjonalna do wartości prędkości.
3. wartość pędu cząstki rośnie ze wzrostem wartości prędkości.
4. wartość pędu cząstki maleje ze wzrostem wartości prędkości.

Zadanie 4. (SP05)

W laboratorium fizycznym przeprowadzono doświadczenia, podczas których zaobserwowano dyfrakcję wiązek: światła, elektronów, neutronów. Doświadczenia te potwierdzają, że

1. wszystkie wiązki użyte w doświadczeniu są falami elektromagnetycznymi.
2. wszystkie wiązki przenoszą ładunek.
3. wiązki te można opisać za pomocą teorii korpuskularnej i teorii falowej.
4. żadna z tych wiązek nie wywołuje zjawiska fotoelektrycznego.

Zadanie 5. (SP05)

Zadanie 6. (SP05)

Europejskie Laboratorium Fizyki Cząstek Elementarnych CERN znajduje się na granicy francusko . szwajcarskiej niedaleko Genewy. Z poniżej zamieszczonych stwierdzeń wybierz nieprawdziwe.

1. CERN jest największym międzynarodowym ośrodkiem badawczym fizyki cząstek w Europie.
2. W CERN.ie za pomocą akceleratorów i detektorów cząstek bada się strukturę materii.
3. Badania przeprowadzane w CERN-ie mają na celu uzyskanie odpowiedzi na pytanie, co działo się z materią w czasie Wielkiego Wybuchu.
4. W CERN.ie prowadzi się obserwacje astronomiczne.

Zadanie 7. (SP05)

Satelita geostacjonarny porusza się wokół Ziemi po orbicie o promieniu około 42000 km.

Oszacuj wartość prędkości liniowej, z jaką porusza się satelita.

Zadanie 8. (SP05)

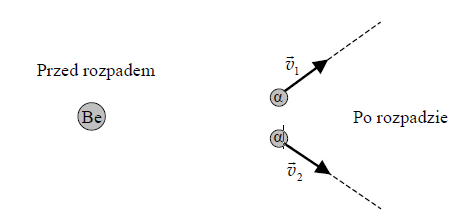
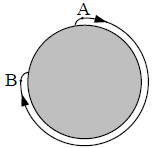
Spoczywające jądro berylu ⁸Be uległo rozpadowi na dwie cząstki α.

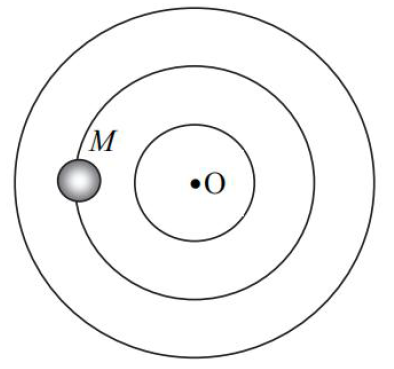
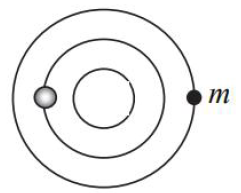
Określ, czy po rozpadzie jądra berylu powstałe cząstki α mogą poruszać się, tak jak pokazano to na rysunku? Uzasadnij swoją odpowiedź.

Zadanie 9. (SP05)

Prędkość w ruchu jednostajnie przyspieszonym można obliczyć, posługując się wzorem:

v²= vo² + 2as

gdzie: v . prędkość w danej chwili, vo . prędkość początkowa, a . przyspieszenie, s . droga.

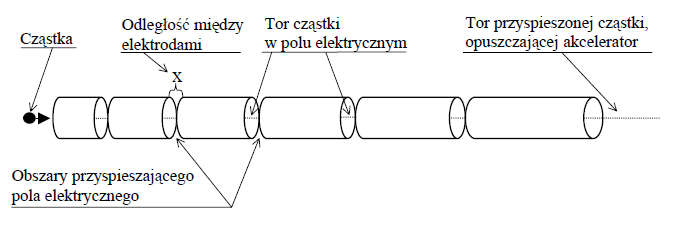
W akceleratorze liniowym w celu zwiększenia prędkości naładowanej cząstki przepuszcza się ją przez jednakowe obszary pola elektrycznego, wytworzonego pomiędzy metalowymi elektrodami w kształcie rur. Przyjmij, że prędkość początkowa cząstki wprowadzonej do akceleratora jest tak mała, że możemy ją uznać za równą zeru.

Zadanie 10. (SP05)

Proton, którego długość fali de Broglie.a wynosi 10-11 m, wpada w obszar jednorodnego pola magnetycznego i porusza się w nim po okręgu o promieniu 2·10-2 m. Oblicz wartość indukcji magnetycznej tego pola. Pomiń efekty relatywistyczne.

Zadanie 11. (SP05)

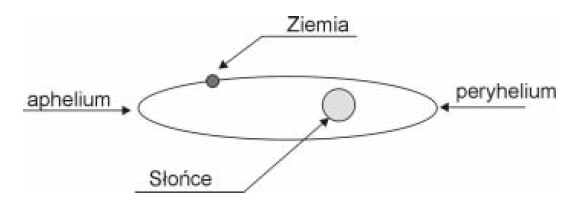
Ziemia, podczas ruchu wokół Słońca po eliptycznej orbicie, raz znajduje się najbliżej Słońca (peryhelium), a raz najdalej (aphelium).

Zapisz, w którym punkcie orbity wartość prędkości liniowej Ziemi jest największa, a w którym najmniejsza? Uzasadnij odpowiedź.

Zadanie 12. (SP05)

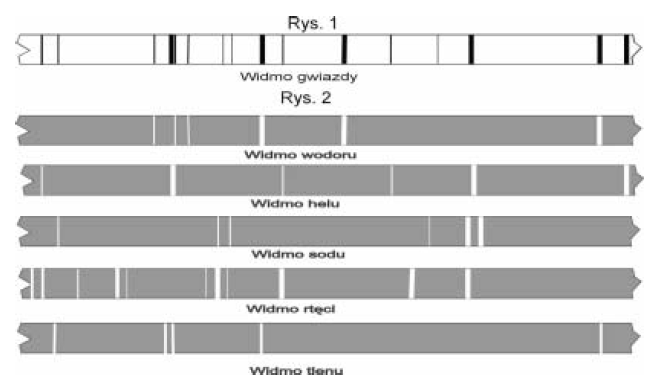
Na rys. 1. przedstawiono linie spektralne w widmie absorpcyjnym odległej gwiazdy otrzymane za pomocą spektrografu siatkowego. Poniżej na rys. 2. zamieszczono widma emisyjne charakterystyczne dla wybranych atomów.

Po analizie widma gwiazdy i widm emisyjnych atomów stwierdzono, że w składzie chemicznym gwiazdy występują atomy wodoru i helu. Wyjaśnij, na czym polega analiza widmowa i dlaczego można było zapisać taki wniosek.

Zadanie 13. (SP06)

Zadanie 14. (SP06)

Energia elektromagnetyczna emitowana z powierzchni Słońca powstaje w jego wnętrzu w procesie

1. syntezy lekkich jąder atomowych.
2. rozszczepienia ciężkich jąder atomowych.
3. syntezy związków chemicznych.
4. rozpadu związków chemicznych.

Zadanie 15. (SP06)

Optyczny teleskop Hubble’a krąży po orbicie okołoziemskiej w odległości około 600 km od powierzchni Ziemi. Umieszczono go tam, aby

1. zmniejszyć odległość do fotografowanych obiektów.
2. wyeliminować zakłócenia elektromagnetyczne pochodzące z Ziemi.
3. wyeliminować wpływ czynników atmosferycznych na jakość zdjęć.
4. wyeliminować działanie sił grawitacji.

Zadanie 16. (SP06)

Satelita krąży po orbicie kołowej wokół Ziemi. Podaj, czy następujące stwierdzenie jest prawdziwe:

„Wartość prędkości liniowej tego satelity zmaleje po przeniesieniu go na inną orbitę kołową o większym promieniu”.

Odpowiedź uzasadnij, odwołując się do odpowiednich zależności.

Zadanie 17. (SP06)

Wykres przedstawia przybliżoną zależność energii wiązania jądra przypadającej na jeden nukleon od liczby masowej jądra.

17.1

Oblicz wartość energii wiązania jądra izotopu radonu (Rn) zawierającego 86 protonów i 134 neutrony. Wynik podaj w megaelektronowoltach.

17.2

Wyjaśnij krótko pojęcie jądrowego niedoboru masy („deficytu masy”). Zapisz formułę matematyczną pozwalającą obliczyć wartość niedoboru masy, jeśli znana jest energia wiązania jądra.

Zadanie 18. (SP07)

Zasada nieoznaczoności Heisenberga stwierdza, że

1. im dokładniej ustalimy wartość pędu cząstki, tym dokładniej znamy jej położenie.
2. im dokładniej ustalimy wartość pędu cząstki, tym mniej dokładnie znamy jej położenie.
3. nie ma związku pomiędzy dokładnościami ustalenia wartości pędu i położenia cząstki.
4. im mniej dokładnie znamy wartość pędu cząstki, tym mniej dokładnie możemy ustalić jej położenie.

Zadanie 19. (SP07)

Trzy czwarte początkowej liczby jąder pewnego izotopu promieniotwórczego ulega

rozpadowi w czasie 24 godzin. Okres połowicznego rozpadu tego izotopu jest równy

1. 2 godziny.
2. 4 godziny.
3. 8 godzin.
4. 12 godzin.

Zadanie 20. (SP07)

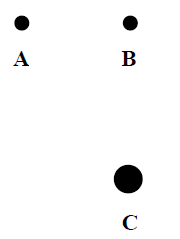
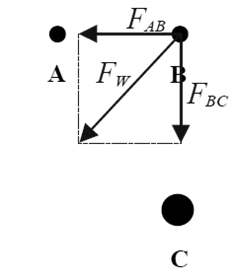
Dwie małe jednorodne kule A i B o jednakowych masach umieszczono w odległości 10 cm od siebie. Kule te oddziaływały wówczas siłą grawitacji o wartości 6,67·10-9 N. Obok tych kul umieszczono małą jednorodną kulę C tak, jak pokazano na rysunku (widok z góry). Masa kuli C jest czterokrotnie większa od masy kuli B, a odległość pomiędzy kulą B i C wynosi 20 cm.

Oblicz wartość wypadkowej siły grawitacji działającej na kulę B.

Zadanie 21. (SP07)

Zadanie 22. (SP07)

Planuje się, że do 2020 roku zostanie założona na powierzchni Marsa baza dla kosmonautów. Większość czasu podczas lotu na Marsa statek kosmiczny będzie podróżował z wyłączonymi silnikami napędowymi.

22.1

Ustal, czy podczas lotu na Marsa (z wyłączonymi silnikami) kosmonauci będą przebywali w stanie nieważkości. Odpowiedź krótko uzasadnij, odwołując się do praw fizyki.

22.2

Wykaż, korzystając z danych w tabeli i wykonując niezbędne obliczenia, że dla księżyców Marsa spełnione jest III prawo Keplera.

Zadanie 23. (SP07)

Elektron w atomie wodoru przechodzi z orbity drugiej na pierwszą. Atom emituje wówczas światło, którego długość fali w próżni wynosi 1,22⋅10-7 m.

23.1

Oblicz częstotliwość fali wysyłanej podczas tego przejścia.

23.2

Oblicz energię emitowanego fotonu. Wynik podaj w eV.

Zadanie 24. (SP07)

1. ………………………………………………………………………………………………………………………………
2. ………………………………………………………………………………………………………………………………
3. ………………………………………………………………………………………………………………………………

Zadanie 25. (SP07)

Elektrony w kineskopie telewizyjnym są przyspieszane napięciem 14 kV.

Oblicz długość fali de Broglie′a dla padającego na ekran elektronu. Efekty relatywistyczne pomiń.

Zadanie 26. (SP07)

Oblicz minimalną wartość pędu fotonu, który padając na wykonaną z cezu katodę fotokomórki spowoduje przepływ prądu. Praca wyjścia elektronów z cezu wynosi 2,14 eV.

Zadanie 27. (SP08)

Ziemia pozostaje w spoczynku względem

1. Słońca.
2. Księżyca.
3. Galaktyki.
4. satelity geostacjonarnego.

Zadanie 28. (SP08)

Ziemia krąży wokół Słońca w odległości w przybliżeniu 4 razy większej niż Merkury. Korzystając z trzeciego prawa Keplera można ustalić, że okres obiegu Ziemi wokół Słońca jest w porównaniu z okresem obiegu Merkurego dłuższy około

1. 2 razy.
2. 4 razy.
3. 8 razy.
4. 16 razy.

Zadanie 29. (SP08)

Jądro izotopu uległo rozpadowi promieniotwórczemu. Powstało nowe jądro zawierające o jeden proton więcej i o jeden neutron mniej niż jądro wyjściowe. Przedstawiony powyżej opis dotyczy rozpadu

1. alfa.
2. gamma.
3. beta plus.
4. beta minus.

Zadanie 30. (SP08)

Przyrząd służący do uzyskiwania i obserwacji widma promieniowania elektromagnetycznego to

1. kineskop.
2. mikroskop.
3. oscyloskop.
4. spektroskop.

Zadanie 31. (SP08)

Oblicz końcową, relatywistyczną wartość pędu elektronu przyspieszanego w akceleratorze do prędkości 0,8 c. Załóż, że początkowa wartość prędkości przyspieszanego elektronu jest znikomo mała.

Zadanie 32. (SP08)

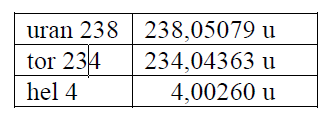
Jądro uranu (92U) rozpada się na jądro toru (Th) i cząstkę alfa.

W tabeli obok podano masy atomowe uranu, toru i helu.

32.1

Zapisz, z uwzględnieniem liczb masowych i atomowych, równanie rozpadu jądra uranu.

32.2

Oblicz energię wyzwalaną podczas opisanego powyżej rozpadu jądra. Wynik podaj w MeV.

W obliczeniach przyjmij, że 1 u ↔ 931,5 MeV.

Zadanie 33. (SP08)

Wyjaśnij, dlaczego astronomowie i kosmolodzy prowadząc obserwacje i badania obiektów we Wszechświecie, obserwują zawsze stan przeszły tych obiektów.

Zadanie 34. (SP09)

Poniżej przedstawiono informacje dotyczące masy (M) jądra berylu ⁹₄Be . Wskaż, która z informacji jest prawdziwa. (przez mp i mn oznaczono odpowiednio masę swobodnego protonu i masę swobodnego neutronu)

1. M > 4 mp + 5 mn
2. M < 4 mp + 5 mn
3. M = 4 mp + 9 mn
4. M = 4 mp + 5 mn

Zadanie 35. (SP09)

Satelita krąży wokół Ziemi po orbicie kołowej. Jeżeli satelita ten zostanie przeniesiony na orbitę kołową o dwukrotnie większym promieniu, to wartość jego prędkości liniowej na tej orbicie

1. wzrośnie 2 razy.
2. wzrośnie 2 razy.
3. zmaleje 2 razy.
4. zmaleje 2 razy.

Zadanie 36. (SP09)

Proton i cząstka alfa poruszają się w próżni z prędkościami o tych samych wartościach.

Długości fal de Broglie’a odpowiadające protonowi (λp) i cząstce alfa (λα) spełniają zależność

1. λα ≅ 0,25 λp
2. λα ≅ 0,5 λp
3. λα ≅ 2 λp
4. λα ≅ 4 λp

Zadanie 37.  (SP09)

Laser helowo neonowy o mocy 0,02 W wysyła w ciągu jednej sekundy 6,35·10¹⁶ fotonów .Oblicz długość fali światła emitowanego przez ten laser.

Zadanie 38. (SP09)

38.1

Zapisz równanie opisanej reakcji rozpadu.

38.2

Zadanie 39. (SP09)

W tabeli przedstawiono wartości całkowitej energii atomu wodoru (En) oraz promieni orbit (rn), po których elektron może się poruszać w zależności od numeru orbity (n).

39.1

Uzupełnij tabelę, wykonując konieczne obliczenia.

39.2

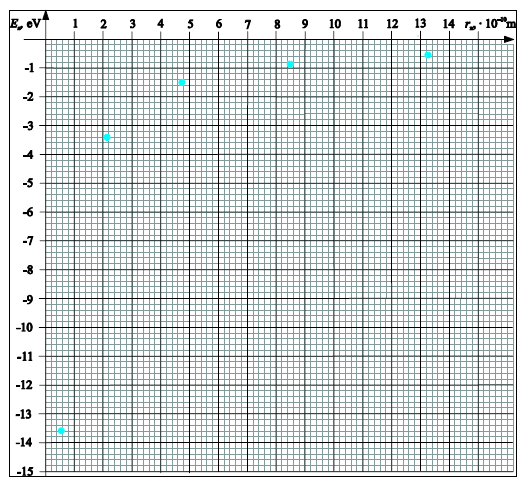
Przedstaw na wykresie związek energii atomu wodoru z promieniem orbity. Uwzględnij fakt, że energia atomu jest skwantowana.

39.3

Korzystając z postulatu Bohra, oblicz wartość prędkości elektronu na pierwszej orbicie.

Zadanie 40. (SP09)

Gwiazda Syriusz B to biały karzeł, a Aldebaran to czerwony olbrzym. W tabeli przedstawiono wybrane informacje dotyczące tych gwiazd.

40.1

Oblicz energię wypromieniowywaną w czasie 1h przez białego karła opisanego w tabeli, wiedząc, że całkowita moc promieniowania Słońca wynosi 3,83·10²⁶ W.

40.2

Zadanie 41. (SP10)

W satelicie krążącym po kołowej orbicie na wysokości znacznie mniejszej od promienia Ziemi, uruchomiony został silnik i wartość prędkości względem Ziemi wzrosła do 11,2 km/h.

Satelita ten

1. będzie poruszał się po orbicie eliptycznej wokół Ziemi.
2. będzie dalej poruszał się po tej samej orbicie wokół Ziemi.
3. opuści orbitę okołoziemską a następnie naszą Galaktykę.
4. opuści orbitę okołoziemską i pozostanie w Układzie Słonecznym.

Zadanie 42. (SP10)

Jednym z izotopów stosowanych do sterylizacji żywności jest izotop kobaltu ⁶⁰₂₇Co. Jest to izotop nietrwały i ulega samorzutnie przemianie β –. Wskutek tego rozpadu powstaje jądro pierwiastka, którego liczba protonów w jądrze wynosi

A. 26.

B. 28.

C. 32.

D. 33.

Zadanie 43. (SP10)

Spośród przedstawionych poniżej zestawów jednostek wybierz ten, który zawiera tylko podstawowe jednostki układu SI.

1. mila, kilogram, godzina
2. kilometr, gram, godzina
3. metr, kilogram, sekunda
4. centymetr, gram, sekunda

Zadanie 44. (SP10)

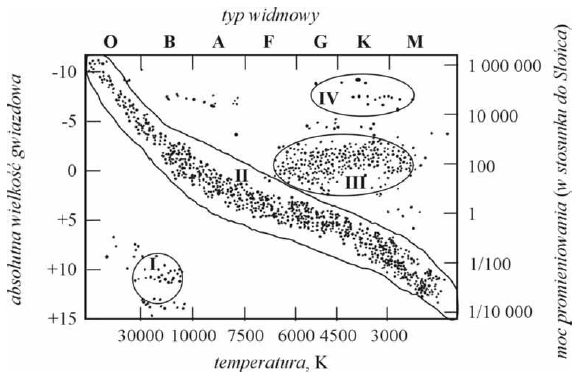
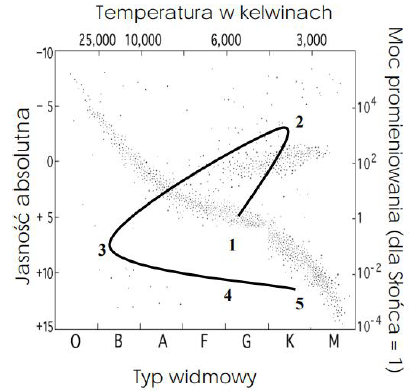
Wszystkie gwiazdy podzielone zostały na 7 zasadniczych typów widmowych. Oznaczone zostały one wielkimi literami O, B, A, F, G, K, M, których kolejność odpowiada malejącej temperaturze gwiazd. Gwiazdami należącymi do typów K i M mogą być

1. pulsary.
2. białe karły.
3. czarne dziury.
4. czerwone olbrzymy.

Zadanie 45. (SP10)

W najnowszych nagrywarkach i odtwarzaczach stosuje się tzw. błękitny laser (Blue Ray). Dotychczas w urządzeniach tych wykorzystywano lasery czerwone, które emitują fale o długości 605 nm. Fale wytwarzane przez błękitny laser są krótsze, mają długość 405 nm, co pozwala zapisywać więcej danych na jednej płycie.

45.1

Oblicz, ile razy energia jednego kwantu promieniowania wysyłanego przez błękitny laser jest większa od energii jednego kwantu wysyłanego przez laser czerwony.

45.2

Wiązkę światła z błękitnego lasera skierowano prostopadle na siatkę dyfrakcyjną, na której wykonano 500 szczelin na 1 mm długości siatki. Ustal najwyższy rząd widma, który można uzyskać za pomocą takiej siatki dyfrakcyjnej.

Zadanie 46. (SP10)

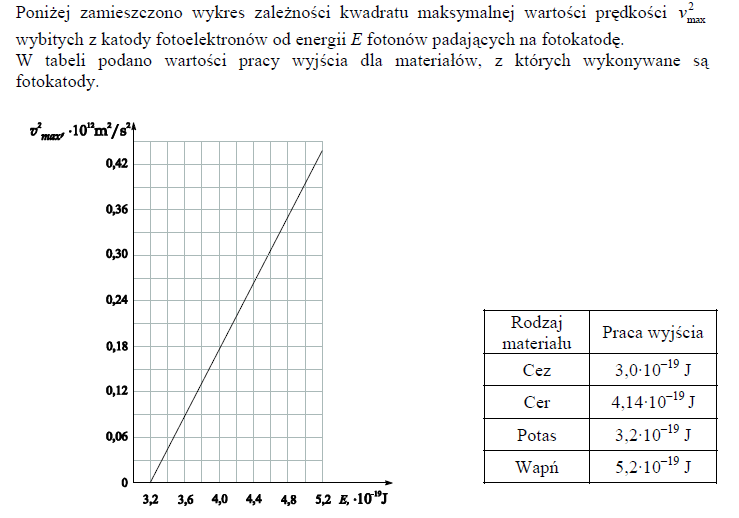
46.1

Ustal, analizując wykres, z jakiego materiału wykonano fotokatodę. Podkreśl w tabeli obok wykresu nazwę tego materiału.

46.2

Wyprowadź wzór, za pomocą którego można obliczyć wartości liczbowe konieczne do wykonania powyższego wykresu. Przyjmij, że znane są energie padających fotonów i praca wyjścia materiału fotokatody.

Zadanie 47. (SP10)

47.1

Korzystając z podanych informacji, uzupełnij poniższe równania reakcji.

47.2

Zadanie 48. (SP10)

Akcelerator to urządzenie, w którym można przyśpieszać do dużych prędkości cząstki obdarzone ładunkiem elektrycznym.

48.1

Bardzo często przyspieszanymi w akceleratorach cząstkami są jony. Uzupełnij poniższe zdania, wpisując właściwe dokończenia spośród niżej podanych.

(przyspiesza jony, zakrzywia tor ruchu jonów).

W akceleratorze pole elektryczne …………………………………………………………………………………..,

a pole magnetyczne ……………………………………………………………………………………

48.2

Oblicz wartość prędkości, jaką uzyskał jon przyspieszany w akceleratorze, jeśli wartość stosunku p/p0 wynosi 5/4 (p – wartość pędu obliczana relatywistycznie, p0 – wartość pędu obliczana klasycznie).

Zadanie 49. (SP10)

Ruch obrotowy Ziemi wokół własnej osi powoduje zmianę wartości ciężaru ciała na różnych szerokościach geograficznych.

Ustal i podkreśl w zamieszczonej poniżej tabeli, w którym miejscu wpływ ruchu obrotowego Ziemi wokół własnej osi na ciężar ciała jest największy.

Zadanie 50. (SP11)

Ludzie poszukujący silnych wrażeń mogą wykonać skok spadochronowy z asekuracją instruktora, do którego skaczący „pasażer” jest w czasie lotu przypięty od spodu. Zaraz po opuszczeniu samolotu, przed otwarciem spadochronu, siła wzajemnego oddziaływania skoczków (przekazywana przez pasy ich spinające) jest

1. równa ciężarowi pasażera.
2. nieco większa od ciężaru pasażera.
3. nieco mniejsza od ciężaru pasażera.
4. bliska zeru.

Zadanie 51. (SP11)

Izotopami nazywamy

1. wszystkie atomy, w których liczba elektronów jest mniejsza od liczby protonów.
2. wszystkie naturalne pierwiastki promieniotwórcze.
3. jądra o tych samych liczbach neutronów, ale różnych liczbach atomowych.
4. jądra o tych samych liczbach atomowych, ale o różnych liczbach neutronów.

Zadanie 52. (SP11)

Księżyc stale zwraca ku Ziemi tę samą stronę, druga strona może być obserwowana tylko przez okrążające Księżyc sondy kosmiczne. Odwrotna strona Księżyca

1. jest stale oświetlona promieniami słonecznymi.
2. nigdy nie jest oświetlona promieniami słonecznymi.
3. jest częściowo oświetlona promieniami słonecznymi, a wielkość części oświetlonej zależy od fazy Księżyca.
4. jest częściowo oświetlona promieniami słonecznymi, a wielkość części oświetlonej zależy od pory roku.

Zadanie 53. (SP11)

Diagram H–R (Hertzsprunga–Russella) pozwala

1. klasyfikować gwiazdy.
2. klasyfikować galaktyki.
3. określać lub szacować wiek Wszechświata.
4. określać lub szacować rozmiary Wszechświata.

Zadanie 54. (SP11)

Planetoida Ida ma własnego satelitę o nazwie Daktyl, którego średnica wynosi 1,4 km. Daktyl krąży po orbicie w przybliżeniu kołowej o promieniu 108 km z okresem obiegu około 37 godzin. Odkryto go podczas przelotu sondy Galileo (28 sierpnia 1993 roku).

54.1

Wykaż, że prędkość Daktyla na orbicie wynosi około 5,1 m/s.

 54.2

Na podstawie podanych informacji oblicz masę planetoidy Ida. Przyjmij, że planetoidę można traktować jako obiekt punktowy (pomiń jej kształt i rozmiary).

Zadanie 55. (SP11)

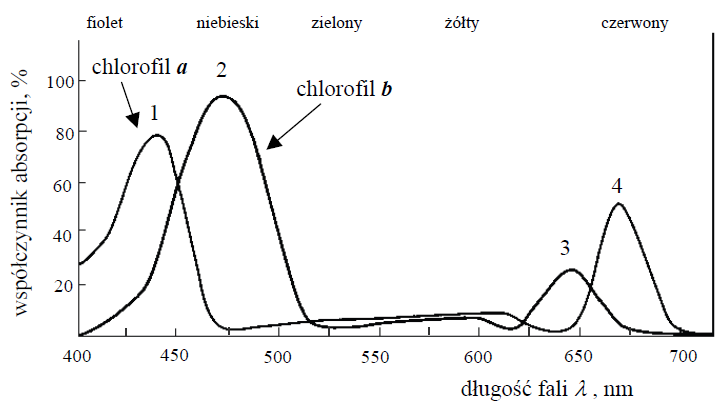
Poniższy wykres przedstawia zależność współczynnika absorpcji od długości fali promieniowania dla dwóch rodzajów chlorofilu. Na osi pionowej wykresu odłożono współczynnik absorpcji światła, tzn. stosunek pochłoniętej energii promieniowania świetlnego do energii promieniowania padającego, wyrażony w procentach.

55.1

Odczytaj z wykresu i zapisz długość fali światła, które chlorofil a pochłania w obszarze krótkofalowym widma w maksymalnym stopniu.

55.2

Zapisz numer tego maksimum absorpcji spośród czterech zaznaczonych na wykresie, dla którego energia jednego fotonu jest najmniejsza. Uzasadnij swój wybór.

55.3

Korzystając z powyższego wykresu, wyjaśnij, dlaczego chlorofil nadaje roślinom zieloną barwę.

Zadanie 57. (SP11)

Rakieta wynosząca satelitę na orbitę ma całkowitą masę startową 3,0⋅106 kg. Podczas pracy silników wyrzucane są z prędkością 2500 m/s gazy spalinowe w ilości 13000 kg w ciągu sekundy. Siła ciągu silników wynosi 3,25⋅107 N. Przyspieszenie ziemskie ma wartość 10 m/s2.

57.1

Oblicz przyspieszenie rakiety podczas startu.

57.2

Czy przyspieszenie rakiety po starcie w miarę upływu czasu będzie rosło, malało, czy też pozostanie stałe? Napisz odpowiedź i ją uzasadnij.

Zadanie 60 (SP11)

60.1

Zapisz równanie przemiany jądra jodu w jądro ksenonu.

60.2

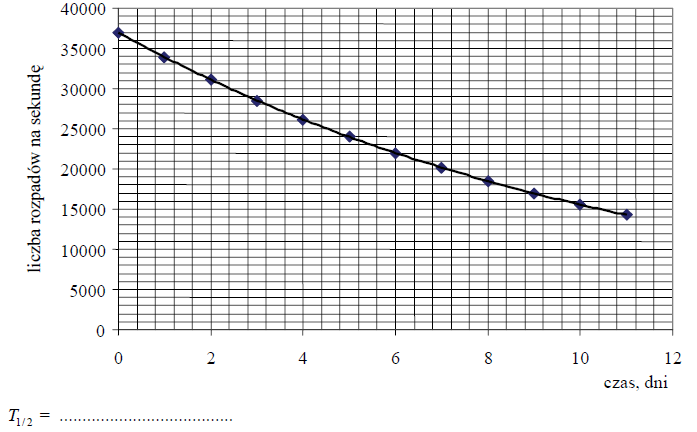
Poniższy wykres przedstawia zależność liczby rozpadów w próbce od czasu. Wyznacz na jego podstawie okres połowicznego zaniku tego izotopu jodu.

60.3

Początkowa masa promieniotwórczego izotopu jodu wynosi 8·10–11 g. Korzystając z wykresu, wyznacz masę jodu po 6 dniach.

Zadanie 61. (SP12)

Sztuczny satelita Ziemi porusza się z prędkością v po orbicie kołowej. Jeśli v1 oznacza wartość pierwszej prędkości kosmicznej, a v2 – drugiej prędkości kosmicznej, to prawidłowa jest relacja

1. v1 < v < v2
2. v1 > v > v2
3. v < v1 < v2
4. v1 < v2 < v

Zadanie 62. (SP12)

Karłowata planeta Pluton porusza się po wydłużonej orbicie eliptycznej. Jej prędkość jest największa przy najmniejszej odległości od Słońca (peryhelium), a najmniejsza przy odległości największej (aphelium). Całkowita energia mechaniczna Plutona jest

1. równa jego maksymalnej energii kinetycznej.
2. jednakowa w każdym punkcie orbity.
3. największa, gdy Pluton jest w aphelium.
4. największa, gdy Pluton jest w peryhelium.

Zadanie 63.  (SP12)

Deterministyczny (przyczynowy) opis zjawisk fizycznych nie stosuje się do

1. całkowitego wewnętrznego odbicia światła.
2. rozpadu α jądra atomowego.
3. ruchu planet wokół Słońca.
4. topnienia lodu.

Zadanie 64.  (SP12)

Para zakochanych o masach 50 kg i 60 kg siedzi na ławce w parku. Odległość między środkami ich mas wynosi 0,6 m.

64.1

Oblicz przybliżoną wartość siły ich wzajemnego oddziaływania grawitacyjnego.

64.2

Wyjaśnij, dlaczego dokładne obliczenie siły oddziaływania grawitacyjnego zakochanych nie jest możliwe, jeśli dysponujemy tylko danymi wymienionymi wyżej i danymi zawartymi w karcie wzorów.

Zadanie 65. (SP12)

Metalowy krążek jest osadzony na główce elektroskopu. Pod wpływem padającego światła nadfioletowego krążek elektryzuje się i dodatkowo ogrzewa.

65.1

a) Wyjaśnij przyczynę elektryzowania się krążka.

 b) Podaj znak ładunku uzyskanego przez krążek. Uzasadnij odpowiedź.

65.2

Jeśli światło pada na krążek przez długi czas, jego ładunek po pewnym czasie przestaje rosnąć (ustala się). Wyjaśnij, dlaczego dalsze naświetlanie krążka nie zwiększa jego ładunku.

65.3

Mikrofale są falami elektromagnetycznymi, których długość jest znacznie większa, niż promieni nadfioletowych. Uzupełnij poniższe zdanie, podkreślając właściwe słowa.

Gdybyśmy zamiast światła nadfioletowego użyli mikrofal, krążek (naelektryzowałby / ogrzałby) się, ale nie (naelektryzował / ogrzał).

Uzasadnij powyższy wybór.

Zadanie 66. (SP12)
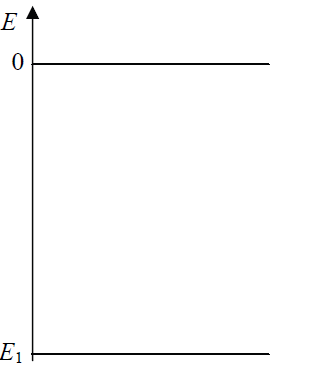
Na przedstawionym rysunku na osi pionowej odłożono energię elektronu w atomie wodoru. W stanie podstawowym elektron ma  najniższą możliwą energię, równą E1 = –13,6 eV.

66.1

Zaznacz linią poziomą na właściwej wysokości pierwszy stan wzbudzony.

66.2

Zaznacz strzałką pionową przejście elektronu odpowiadające jednej z linii w widmie emisyjnym wodoru.

Zadanie 67.  (SP12)

Poniżej zamieszczono obrazy uzyskane na kliszy fotograficznej po skierowaniu wiązki neutronów i wiązki promieni rentgenowskich (jest to krótkofalowe promieniowanie elektromagnetyczne) na kryształ soli kuchennej. Kryształ soli stanowił w doświadczeniach trójwymiarową siatkę dyfrakcyjną. Kliszę fotograficzną umieszczono za kryształem.

67.1

Napisz, o jakiej naturze neutronów świadczy fotografia 1.

67.2

Załóżmy, że układ plamek na obu powyższych fotografiach jest identyczny (co z pewnych drugorzędnych powodów niezupełnie się zgadza z obserwacjami), a pomiar kątów odchylenia wiązki dał dla każdej plamki jednakowe wyniki w obu przypadkach. Uzupełnij poniższe zdanie, wpisując nazwę jednej z wielkości: masa, prędkość, pęd, energia kinetyczna. Wnioskiem z wymienionych obserwacji jest to, że neutrony miały tę samą (ten sam) …………………………, co kwanty promieniowania rentgenowskiego. Uzasadnij swój wybór.

Zadanie 68. (SP13)

Księżyc, naturalny satelita Ziemi, obiega Ziemię po orbicie o promieniu 9 razy większym od promienia orbity sztucznego satelity Ziemi. Zakładając kołowy kształt torów obu satelitów, można stwierdzić, że prędkość orbitalna Księżyca jest, w porównaniu do prędkości orbitalnej sztucznego satelity,

1. 3 razy mniejsza.
2. 3 razy większa.
3. 9 razy mniejsza.
4. 9 razy większa.

Zadanie 69. (SP13)

Które z wymienionych poniżej urządzeń nie służy do przyspieszania cząstek naładowanych?

1. synchrotron
2. cyklotron
3. akcelerator liniowy
4. akumulator

Zadanie 70. (SP13)

Jurij Gagarin przebywał w statku kosmicznym Wostok-1 na orbicie okołoziemskiej ok. 68 minut, co odpowiada torowi od punktu A do punktu B na rysunku obok. Gdyby Gagarin wykonał pełne okrążenie, to trwałoby ono 89 minut. Wysokość lotu orbitalnego nad powierzchnią Ziemi przyjmijmy jako stałą i równą 240 km. Oblicz, z jaką prędkością poruszał się Wostok-1 i jaką przebył drogę.

Zadanie 71. (SP13)

Do sprawdzania banknotów stosuje się lampę wysyłającą promieniowanie ultrafioletowe o mocy 4 W i długości fali 312 nm. Oblicz, ile fotonów wytwarza ta lampa w czasie 1 sekundy.

Zadanie 72. (SP13)

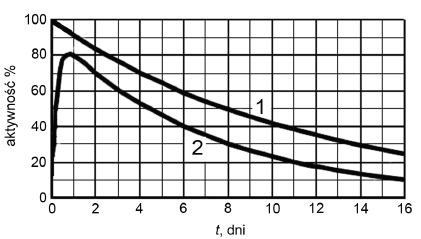
Medycyna nuklearna zajmuje się bezpiecznym zastosowaniem izotopów promieniotwórczych w terapii oraz diagnostyce medycznej. Ważnym parametrem, który decyduje o zastosowaniu izotopu jest jego efektywny czas połowicznego zaniku – czas, w którym aktywność promieniotwórczej substancji w żywym organizmie zmniejsza się do połowy. Na ten efektywny czas połowicznego zaniku wpływa m.in. wydalanie jodu z organizmu. W diagnostyce i leczeniu schorzeń tarczycy stosuje się izotop jodu ¹³¹ I .

Na wykresie przedstawiono zależność aktywności jodu ¹³¹ I od czasu:

1 – zmierzonej w próbce kontrolnej, pozostającej cały czas w probówce.

2 – zmierzonej w tarczycy pacjenta.

72.1

• efektywny czas połowicznego zaniku w tarczycy pacjenta z wykresu 2; zauważ, że maksimum aktywności jodu w tarczycy jest przesunięte.

72.2

Zadanie 73. (SP13)

Pozyton jest antycząstką elektronu, mającą masę równą masie elektronu, a ładunek równy ładunkowi elektronu co do wartości bezwzględnej i przeciwny co do znaku.

73.1

W efekcie zderzenia elektronu z pozytonem następuje zjawisko anihilacji, w wyniku którego te cząstki ulegają przemianie w dwa kwanty promieniowania elektromagnetycznego. Oblicz łączną energię tych kwantów. Przyjmij, że prędkości obu cząstek w chwili zderzenia były niewielkie.

73.2

Oblicz wartość przyspieszenia, z jakim będą poruszać się elektron i pozyton, jeżeli znajdą się one w odległości 1 cm od siebie. Uwzględnij tylko siłę wzajemnego przyciągania elektrostatycznego tych cząstek.

Zadanie 74. (SP14)

Zadanie 75 (SP14)

Dane dotyczące księżyców dwóch planet Układu Słonecznego zamieszczono w tabeli.

Zakładamy, że orbity tych księżyców są okręgami.

75.1

Korzystając z odpowiednich wzorów i praw fizycznych, udowodnij, że wzór pozwalający obliczyć masę M planety w zależności od odległości R księżyca od planety oraz od czasu obiegu T księżyca wokół planety ma postać

75.2

Korzystając ze wzoru podanego w zadaniu 14.1, oblicz, ile razy masa planety II jest większa od masy planety I.

75.3

Planeta I ma – oprócz wymienionego w tabeli – jeszcze jeden księżyc. Odległość tego księżyca od środka planety wynosi 23,5 tys. km. Korzystając z odpowiedniego prawa Keplera, oblicz czas pełnego obiegu tego księżyca wokół planety I.

Zadanie 76 (SP14)

O własnościach substancji, ich budowie wewnętrznej i poziomach energetycznych atomów dowiadujemy się z wyników doświadczeń, takich jak:

1. Badanie zjawiska fotoelektrycznego.
2. Badanie widma emisyjnego gazów.
3. Badanie widma absorpcyjnego gazów.
4. Badanie dyfrakcji elektronów na krysztale.

76.1

Wpisz odpowiednio wszystkie wymienione doświadczenia, które dotyczą:

 wyznaczenia pracy wyjścia dla metalu

………………………………………………………………………………………………..

 badania struktury kryształu

………………………………………………………………………………………………..

 wyznaczenia poziomów energetycznych atomów

……………………………………………………………………………………………….

76.2

Podczas lekcji fizyki nauczyciel przygotował następujące przyrządy:

• rurkę szklaną z dwiema elektrodami, zawierającą rozrzedzony gaz
• zwierciadło wklęsłe
• siatkę dyfrakcyjną
• laser (źródło światła monochromatycznego)
• ekran
• źródło wysokiego napięcia
• przesłonę ze szczeliną.

Zadaniem uczniów było zaprojektowanie doświadczenia polegającego na obserwowaniu widma emisyjnego gazu. Napisz, które z przygotowanych przyrządów powinni wybrać uczniowie do wykonania doświadczenia.

Zadanie 77(SP14)

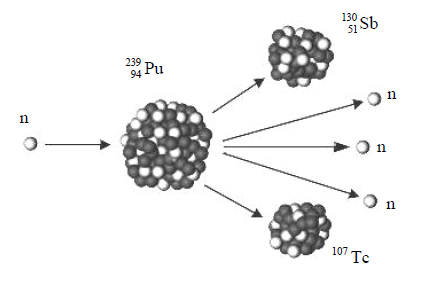
Poniższy rysunek przedstawia sytuację zapoczątkowaną wniknięciem neutronu w głąb jądra plutonu.

77.1

Napisz nazwę reakcji jądrowej przedstawionej na tym rysunku.

77.2

Zapisz równanie reakcji przedstawionej na rysunku, uwzględniając liczby masowe i liczby atomowe (porządkowe) wszystkich jąder i cząstek.

Zadanie 78. (NP15)

Syriusz B jest białym karłem, a więc gwiazdą o wysokiej temperaturze oraz

1. dużej mocy promieniowania i dużej gęstości.
2. małej mocy promieniowania i dużej gęstości.
3. dużej mocy promieniowania i małej gęstości.
4. małej mocy promieniowania i niewielkiej gęstości.

Zadanie 79. (NP15)

W tabelce podane są informacje dotyczące Księżyca.

 79.1

Wykaż, że wartość prędkości Księżyca na orbicie wokół Ziemi jest około 7,8 razy mniejsza od wartości pierwszej prędkości kosmicznej dla Ziemi.

79.2

Oblicz wartość siły, z jaką Księżyc przyciąga pojazd księżycowy o masie 50 kg. Przyjmij, że Księżyc jest jednorodną kulą.

Zadanie 80. (NP15)

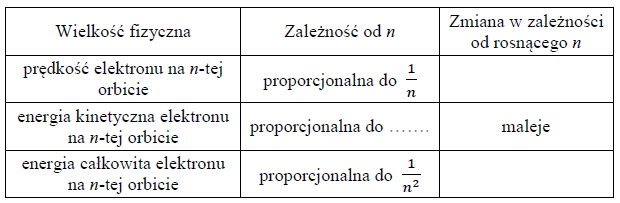
Skwantowanie wielkości fizycznych w modelu Bohra opisującym budowę atomu wodoru można zapisać wzorami na prędkość elektronu, jego energię kinetyczną lub energię całkowitą.

Skwantowanie oznacza, że dana wielkość fizyczna może przyjmować wyłącznie określone wartości liczbowe, w zależności od liczby naturalnej n.

80.1

Uzupełnij tabelę: wstaw w zakropkowane miejsce w środkowej kolumnie wyrażenie zawierające n, a w wolnych miejscach prawej kolumny wpisz określenia zmiany (rośnie, maleje lub nie zmienia się).

80.2

Oblicz energię emitowaną przez atom wodoru podczas przeskoku elektronu z orbity czwartej na orbitę drugą. Energia jonizacji atomu wodoru dla stanu podstawowego jest równa 13,6 eV.

Zadanie 81. (NP15)

81.1

81.2

 81.3

Uzupełnij tabelę, wpisując symbol odpowiedniego izotopu.

Zadanie 82. (NP16)

Pierwsze cztery planety Układu Słonecznego według rosnącej odległości od Słońca to:
Merkury, Wenus, Ziemia, Mars. Te same planety uszeregowane według wzrastającej masy to:
Merkury, Mars, Wenus, Ziemia. Jeżeli przyjmiemy, że planety poruszają się po orbitach kołowych, to poprawną relacją między prędkościami liniowymi tych planet jest

1. vMer < vWen < vZiem < vMars
2. vMer > vWen > vZiem > vMars
3. vMer < vMars < vWen < vZiem
4. vMer > vMars > vWen > vZiem

Zadanie 83. (NP16)

Jedną z zalet umieszczenia teleskopu optycznego na orbicie okołoziemskiej w porównaniu z obserwacjami z powierzchni Ziemi jest to, że

1. do teleskopu na orbicie nie docierają fale radiowe wytwarzane przez ludzi, które na Ziemi zakłócają odbiór sygnałów.
2. promieniowanie kosmiczne może być wykorzystane do zasilania urządzeń teleskopu.
3. w atmosferze Ziemi występują drgania powietrza, które zakłócają bieg promieni świetlnych.
4. w ten sposób zbliżamy teleskop do planet i gwiazd, co powiększa otrzymywane obrazy.

Zadanie 84. (NP16)

Według modelu Bohra elektrony krążą wokół jądra pod wpływem sił

1. elektrycznych.
2. magnetycznych.
3. grawitacyjnych.
4. jądrowych.

Zadanie 85. (NP16)

Deterministycznego (przyczynowego) opisu przyrody nie potwierdza

1. całkowite wewnętrzne odbicie światła.
2. rozpad α jąder atomowych.
3. ruch planet wokół Słońca.
4. topnienie lodu.

Zadanie 86. (NP16)

W szklanej bańce próżniowej umieszczono dwie metalowe płytki (P i Q) wykonane z tego samego materiału, które połączono ze źródłem napięcia tak, jak pokazano na rysunku obok. W obwód włączono czuły amperomierz. Gdy jedną z płytek oświetlono, amperomierz wskazał przepływ prądu w obwodzie, natomiast podczas oświetlania drugiej płytki tym samym strumieniem światła przepływ prądu nie nastąpił.

86.1

a) Wyjaśnij, dlaczego w pierwszym przypadku w obwodzie nastąpił przepływ prądu.
b) Napisz, którą płytkę oświetlono, gdy w obwodzie popłynął prąd. Uzasadnij dokonany wybór.

86.2.

Oblicz maksymalną długość fali promieniowania, które może spowodować przepływ prądu w przedstawionym obwodzie. Przyjmij, że płytki wykonane są z metalu, dla którego praca wyjścia wynosi 7,2·10^–19 J.

Zadanie 87. (NP16)

Zadanie 88. (NP16)

Poniżej przedstawiono schemat reakcji jądrowej.

Napisz nazwę cząstki X i uzasadnij swoją decyzję.

Zadanie 89. (NP16)

Hipoteza Wielkiego Wybuchu jest obecnie powszechnie przyjętym przez astrofizyków opisem początków Wszechświata. Zgodnie z tą hipotezą około 14 miliardów lat temu cała obecnie obserwowana materia Wszechświata była bardzo gorąca i skupiona w niewielkim obszarze przestrzeni. Podaj jeden z dostępnych dzisiaj faktów obserwacyjnych potwierdzających hipotezę Wielkiego Wybuchu.

Zadnie 90.  (NP17)

Jeżeli różne jądra atomowe wpadają w to samo pole magnetyczne z taką samą prędkością skierowaną prostopadle do linii pola magnetycznego, to po okręgu o najmniejszym promieniu będzie poruszać się jądro

Zadanie 91. (NP17)

Na skutek pochłonięcia fotonu przez atom wodoru elektron przeszedł z orbity pierwszej, odległej od jądra o w przybliżeniu 50 pm, na orbitę drugą. Odległość elektronu od jądra wzrosła do

1. 100 pm
2. 150 pm
3. 200 pm
4. 250 pm

Zadanie 92. (NP17)

Na katodę fotokomórki pada światło o ustalonej częstotliwości, wysyłane przez laser.
W wyniku tego przez fotokomórkę płynie prąd. Jeżeli zwiększymy natężenie światła lasera, to

1. wzrośnie natężenie prądu płynącego przez fotokomórkę.
2. zmniejszy się praca wyjścia elektronów wybijanych z katody.
3. natężenie prądu płynącego przez fotokomórkę zmaleje do zera.
4. wzrośnie energia elektronów wybijanych z katody fotokomórki.

Zadanie 93. (NP17)

Niedoborem (deficytem) masy jądra atomowego nazywamy różnicę pomiędzy

1. masą protonu a masą neutronu.
2. sumą mas protonów a sumą mas neutronów tworzących jądro atomowe.
3. sumą mas nukleonów tworzących jądro atomowe a masą jądra atomowego.
4. masą atomu a masą jego jądra.

Zadanie 94. (NP17)

Zadanie 95.  (NP17)

Średnia odległość od Słońca do Marsa jest 1,524 razy większa niż średnia odległość od Słońca do Ziemi. Średnia odległość planety od Słońca oznacza długość półosi wielkiej orbity eliptycznej, po której ta planeta okrąża Słońce. Oblicz, korzystając z prawa Keplera, ile dni ziemskich trwa obieg Marsa wokół Słońca.

Zadanie 96.  (NP17)

Jądro izotopu radu ²²⁴Ra ulega rozpadowi alfa z czasem połowicznego zaniku około 3,7 dnia, zgodnie ze schematem:

Suma mas jądra radonu i jądra helu jest o 0,0062 u mniejsza od masy jądra radu, gdzie u jest jednostką masy atomowej.

96.1

Udowodnij, że w układzie odniesienia, w którym jądro radu spoczywało, stosunek energii kinetycznej uzyskanej przez jądro ⁴He do energii kinetycznej uzyskanej przez jądro radonu jest równy około 55.

 96.2

Próbkę zawierającą izotop ²²⁴Ra zbadano po upływie 13 dni od dostarczenia do laboratorium i ustalono, że po tym czasie próbka zawierała 0,75 mg tego izotopu. Oszacuj masę tego izotopu w chwili dostarczenia do laboratorium.

Zadanie 97.  (NP17)

Energia elektronu znajdującego się w stanie podstawowym w atomie wodoru wynosi
E₁ = −13,6 eV.

 97.1

Oblicz energię fotonu emitowanego podczas przejścia elektronu w atomie wodoru z orbity trzeciej na drugą.

97.2

Oblicz długość fali promieniowania powstałego podczas przejścia elektronu w atomie wodoru z orbity trzeciej na drugą.

Zadanie 98. (NP18)

Energia fotonu padającego na płytkę metalową jest czterokrotnie większa od pracy wyjścia elektronu z tego metalu. Maksymalna energia kinetyczna, którą może mieć elektron wybity z powierzchni tego metalu, w stosunku do energii fotonu padającego na płytkę, stanowi

1. 12,5%
2. 25%
3. 50%
4. 75%

Zadanie 99. (NP18)

Elektron w atomie wodoru przechodzi ze stanu energetycznego opisanego liczbą kwantową n = 3 do stanu podstawowego. W wyniku tego przejścia emitowany jest foton. Jeżeli energia, jaką ma elektron w stanie podstawowym, wynosi E?= – 13,6 eV, to zgodnie z modelem atomu wodoru według Bohra, energia emitowanego fotonu jest równa:

Zadanie 100. (NP18)

Planety P1 i P2 okrążają pewną gwiazdę po orbitach kołowych. Okres obiegu planety P2 dookoła tej gwiazdy jest 8 razy większy od okresu obiegu planety P1 wokół tej gwiazdy. Z tego wynika, że promień orbity, po której porusza się planeta P2, jest

1. 16 razy większy od promienia orbity, po której porusza się planeta P1.
2. 8 razy większy od promienia orbity, po której porusza się planeta P1.
3. 4 razy większy od promienia orbity, po której porusza się planeta P1.
4. 2 razy większy od promienia orbity, po której porusza się planeta P1.

Zadanie 101. (NP18)

Siły jądrowe działające pomiędzy dwoma protonami są

1. większe od sił elektrycznych działających pomiędzy tymi protonami, niezależnie od odległości pomiędzy nimi.
2. na odległościach rzędu 10-15 m większe od sił elektrycznych działających pomiędzy tymi protonami, a na dużo większych odległościach są mniejsze od sił elektrycznych.
3. mniejsze od sił elektrycznych działających pomiędzy tymi protonami, niezależnie od odległości pomiędzy nimi.
4. na odległościach rzędu 10-15 m mniejsze od sił elektrycznych działających pomiędzy tymi protonami, a na dużo większych odległościach są większe od sił elektrycznych.

Zadanie 102. (NP18)

Średnią odległością ciała niebieskiego od Słońca nazywa się długość wielkiej półosi orbity eliptycznej, po której to ciało krąży wokół Słońca. Ta odległość jest równa połowie odległości od punktu aphelium do punktu peryhelium orbity okołosłonecznej. Aphelium jest punktem na orbicie ciała niebieskiego, który leży w największej odległości od Słońca, natomiast peryhelium jest punktem na orbicie ciała niebieskiego leżącym najbliżej Słońca. Dla orbit kołowych średnia odległość ciała od Słońca jest długością promienia tej orbity. Kometa Halleya okrąża Słońce po bardzo wydłużonej orbicie. Gdy kometa znajduje się w peryhelium orbity, to jej odległość do środka Słońca wynosi 0,59 jednostki astronomicznej, natomiast gdy znajduje się w aphelium – to jej odległość od środka Słońca wynosi 35,08 jednostki astronomicznej.

Na podstawie powyższej informacji oraz trzeciego prawa Keplera oblicz okres obiegu komety Halleya dookoła Słońca. Wynik podaj w latach ziemskich z dokładnością do dziesiętnych części roku.

Zadanie 103. (NP18)

103.1

Uzupełnij liczby atomowe i masowe w poniższym zapisie reakcji rozpadu aktynu. Zapisz, jak nazywa się ten typ rozpadu.

 103.2

Oszacuj, ile czasu potrzeba, aby rozpadło się 94% pierwotnej liczby jąder próbki, która początkowo zawierała wyłącznie aktyn.

103.3

Zadanie 104. (NP18)

W lampie próżniowej napięcie między katodą a anodą wynosi 2 000 V. W wyniku rozgrzania katody do wysokiej temperatury emituje ona 2·1014 elektronów na sekundę. Elektrony przyspieszane dalej w polu elektrycznym padają na anodę. Przyjmij, że prędkości początkowe oderwanych od katody elektronów wynoszą zero.

 104.1

Oblicz stosunek energii kinetycznej elektronu padającego na anodę do jego energii spoczynkowej. Na podstawie tego stosunku ustal, czy w tym przypadku do obliczeń można stosować wzory mechaniki klasycznej, czy może należy stosować wzory mechaniki relatywistycznej. Uzasadnij odpowiedź.

 104.2

Oszacuj natężenie prądu płynącego przez lampę.

Zadanie 105. (NP19)

Na metalową płytkę padł foton o energii 4,6 eV. Ten foton został całkowicie pochłonięty przez elektron znajdujący się w paśmie przewodnictwa tego metalu. W wyniku tego elektron został wybity z powierzchni metalu, a jego energia kinetyczna w chwili tuż po opuszczeniu metalu wynosiła 0,4 eV. Praca wyjścia elektronu z tego metalu wynosi około

1. 6,7·10^–19 J
2. 8·10^–19 J
3. 7,4·10^–19 J
4. 0,64·10^–19 J

Zadanie 106.  (NP19)

Zadanie 107. (NP19)

Pewne jądro atomowe X znajdujące się w stanie o najniższej energii przechodzi do stanu wzbudzonego X* (tzn. stanu o większej energii) na skutek pochłonięcia kwantu promieniowania elektromagnetycznego. Energia wiązania jądra X* w stanie wzbudzonym w porównaniu do energii wiązania jądra w stanie podstawowym jest

1. większa.
2. mniejsza.
3. taka sama.
4. większa lub mniejsza – zależnie od energii pochłoniętego fotonu.

Zadanie 108.  (NP19)

Zadanie 109.  (NP19)

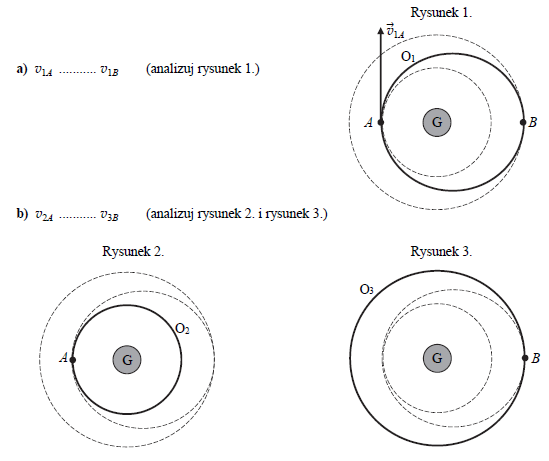
109.1

Poniżej w wykropkowane miejsca wpisz właściwe relacje: większy, równy, mniejszy (>, =, <), między wartościami prędkości planet w danych punktach na poszczególnych orbitach.

109.2
Okresy orbitalne planet poruszających się po orbitach O1, O2 i O3 oznaczymy odpowiednio T1, T2, T3. Wpisz poniżej w każde z wyznaczonych miejsc po jednym z okresów orbitalnych planet tak, aby zapisana relacja między wszystkimi okresami była prawdziwa.

……………….. > …………….. > ……………..

Zadanie 110. (NP19)

Elektron w atomie wodoru znajdował się na trzecim poziomie energetycznym (n = 3). Na ten elektron padł foton o częstotliwości f = 2,33·1014 Hz. Ten foton został całkowicie pochłonięty przez elektron, w wyniku czego elektron przeszedł z poziomu n = 3 na wyższy poziom energetyczny. Energia elektronu na pierwszym poziomie energetycznym w atomie wodoru wynosi E1= –13,6 eV. Określ numer poziomu energetycznego, na który przeszedł elektron w opisanym zjawisku.

Zadanie 111.  (NP19)

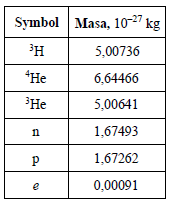
Nietrwały izotop wodoru tryt H₁³ ulega przemianie, w wyniku której powstaje jądro pewnego izotopu helu oraz emitowane są cząstki: elektron oraz antyneutrino elektronowe. Neutrina i antyneutrina mają zerowy ładunek elektryczny, a ich masa w porównaniu do masy elektronu jest pomijalnie mała. Tabela obok przedstawia przybliżone masy wybranych cząstek i jąder. Niektóre z nich wykorzystaj w punkcie b) zadania.

a) Uzupełnij liczby atomowe i masowe w poniższym zapisie reakcji rozpadu trytu. Zapisz, jak nazywa się ten typ rozpadu.

b) Oszacuj całkowitą energię kinetyczną wszystkich produktów przemiany opisanej w zadaniu 19. Masę odpowiednich jąder i cząstek znajdź w tabeli powyżej. Przyjmij, że jądro trytu początkowo spoczywało. Wynik podaj z dokładnością do jednej cyfry znaczącej.

Zadanie 112. (SR05)

Zimą najjaśniejszą gwiazdą naszego nocnego nieba jest Syriusz. Pod tą nazwą kryje się układ dwóch gwiazd poruszających się wokół wspólnego środka masy. Syriusz A jest gwiazdą ciągu głównego, a Syriusz B jest białym karłem i nie można go zobaczyć gołym okiem.

112.1

Na podstawie tekstu i własnej wiedzy wymień dwie charakterystyczne cechy białych karłów.

1. ————————————————————————————————————

2. ————————————————————————————————————

112.2

Średnia gęstość Syriusza B wynosi 2,4⋅10⁹ m/kg³ , a jego promień 5,9⋅10⁶ m. Oblicz wartość przyspieszenia grawitacyjnego na powierzchni Syriusza B, pomijając wpływ Syriusza A.

112.3

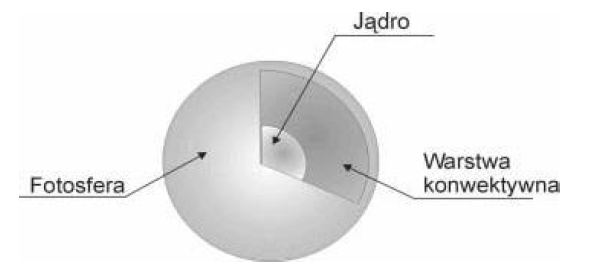
Na rysunku przedstawiono budowę wnętrza Syriusza A.

Energia zawarta w jądrze gwiazdy transportowana jest na powierzchnię przez warstwę konwektywną, a z powierzchni fotosfery wypromieniowana w przestrzeń kosmiczną. Zapisz, czym różni się transport energii w wyniku konwekcji od transportu poprzez promieniowanie.

112.4

Głównym źródłem energii Syriusza A są reakcje termojądrowe polegające na zamianie wodoru w hel za pośrednictwem węgla i tlenu (tzw. cykl CNO).

1. Uzupełnij równanie reakcji będącej częścią cyklu CNO.
   ¹⁴₇ N + …………→¹⁵₈O + γ
2. Poniżej zamieszczono równania dwóch przemian jądrowych cyklu CNO. Obok równań reakcji zapisz nazwę tego typu procesu jądrowego.
   ¹²₆C+₁¹H →¹³₇N + γ              ————————————————————–
   ¹³₇ N →¹³₆C + e⁺                      ————————————————————–

112.5

W zachodzącym w jądrze Syriusza A cyklu CNO najwięcej energii wydziela się podczas reakcji zamiany węgla w azot.

¹³₆C+₁¹H =¹⁴₇N +γ

Oblicz, ile jąder węgla w Syriuszu A musiałoby ulec tego typu reakcji, by wytworzona energia mogła w normalnych warunkach stopić 1 g lodu. Ciepło topnienia lodu wynosi
3,34·10⁵ J/kg. Masy jąder wodoru, węgla i azotu mają wartości odpowiednio równe:

m_H = 1,673⋅10^-27 kg, m_C = 21,586⋅10^-27 kg, m_N = 23,245⋅10^-27 kg

Zadanie 113. (SR05)

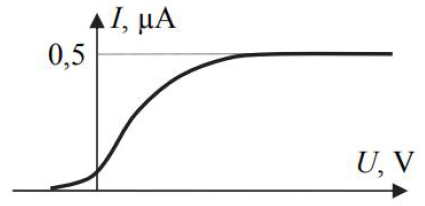
Katoda fotokomórki oświetlana jest wiązką światła laserowego o długości fali 330 nm.

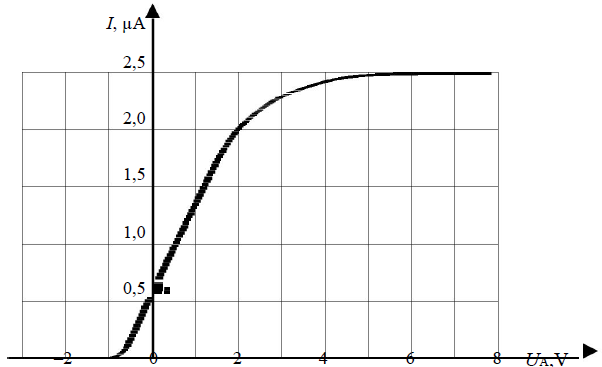
Charakterystykę prądowo-napięciową tej fotokomórki przedstawiono poniżej na wykresie.

113.1

Korzystając z wykresu oblicz (w dżulach) pracę wyjścia elektronów z katody fotokomórki.

113.2

Tę samą fotokomórkę oświetlamy światłem o innej długości fali. Zapisz, jaki warunek musi być spełniony, aby po przyłożeniu odpowiedniego napięcia przez fotokomórkę popłynął prąd?

113.3

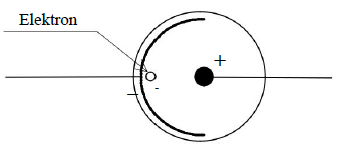
W przestrzeni między elektrodami rozważanej fotokomórki wytworzone jest pole elektryczne.

Katoda jest częścią sfery, a anoda znajduje się w środku tej sfery.

Zapisz, jakim ruchem i po jakim torze  (zaznacz  na  rysunku) będzie  poruszać  się  elektron wybity przez foton, jeżeli jego prędkość początkowa wynosiła zero.

Uzasadnij swoją odpowiedź.

113.4

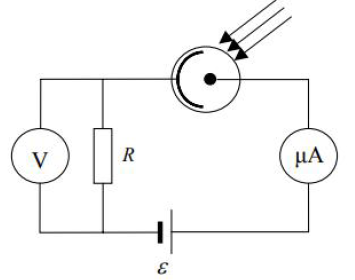
Fotokomórkę włączono w przedstawiony na rysunku obwód prądu elektrycznego.

Woltomierz, mierzący napięcie na zaciskach opornika, wskazał wartość 4 V, a amperomierz 2 µA. Oba przyrządy są idealne (tzn. opór woltomierza jest nieskończenie duży, a opór amperomierza zerowy). Oblicz opór opornika oraz siłę elektromotoryczną źródła prądu. Opór wewnętrzny źródła prądu jest mały więc go pomiń.

Czy zwiększenie siły elektromotorycznej ogniwa spowoduje proporcjonalne zwiększenie natężenia prądu w obwodzie? Odpowiedź uzasadnij.

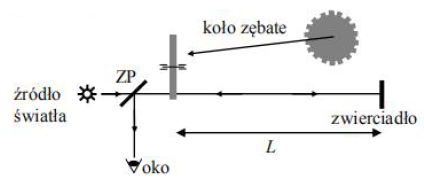
Zadanie 114. (SR06)

W pracowni fizycznej wykonano doświadczenie mające na celu badanie zjawiska fotoelektrycznego i doświadczalne wyznaczenie wartości stałej Plancka. W oparciu o wyniki pomiarów sporządzono poniższy wykres. Przedstawiono na nim zależność maksymalnej energii kinetycznej uwalnianych elektronów od częstotliwości światła padającego na fotokomórkę.

114.1

Odczytaj z wykresu i zapisz wartość częstotliwości granicznej promieniowania dla tej fotokatody.

114.2

Oblicz, korzystając z wykresu, pracę wyjścia elektronów z fotokatody. Wynik podaj w elektronowoltach.

114.3

Oblicz doświadczalną wartość stałej Plancka, wykorzystując tylko dane odczytane z wykresu oraz zależność h ⋅ν = W + E_k .

114.4

Narysuj schemat układu elektrycznego pozwalającego wyznaczyć doświadczalnie wartość napięcia hamowania fotoelektronów. Masz do dyspozycji elementy przedstawione poniżej oraz przewody połączeniowe.

Zadanie 115. (SR06)

Laser o mocy 0,1 W emituje w próżni monochromatyczną wiązkę światła o długości fali 633 nm i kołowym przekroju.

115.1

Oszacuj liczbę fotonów zawartych w elemencie wiązki światła o długości jednego metra.

115.2

Oblicz wartość siły, jaką wywierałaby ta wiązka światła laserowego padająca w próżni prostopadle na wypolerowaną metalową płytkę. Do obliczeń przyjmij, że w ciągu jednej sekundy na powierzchnię płytki pada 10¹⁷ fotonów. Załóż, że płytka odbija w całości padające na nią promieniowanie.

Zadanie 116. (SR07)

Spośród pierwiastków występujących naturalnie w Ziemi największą liczbę atomową ma uran.
W uranie naturalnym występują głównie dwa izotopy ²³⁵U i ²³⁸ W wyniku rozpadów promieniotwórczych uran ²³⁸U przechodzi w tor ²³⁴Th, a następnie w proaktyn ²³⁴Pa.

116.1

Uzupełnij zapisy poniższych reakcji jądrowych.

Rozszczepienie jądra uranu ²³⁵₉₂ U można spowodować bombardując jądra uranu powolnymi neutronami o energii około 1 eV. W reakcji tej uwalnia się energia około 210 MeV.

Jedną z możliwych reakcji rozszczepienia uranu ²³⁵U przedstawiono poniżej: Przez x i y oznaczono odpowiednio liczbę neutronów i liczbę elektronów

116.2

Oblicz liczbę neutronów x oraz liczbę elektronów y, w reakcji rozszczepienia uranu ²³⁵U.

116.3

Oblicz wartość prędkości neutronu wywołującego rozszczepienie uranu ²³⁵U.

116.4

Podaj dwa warunki, które muszą być spełnione, aby w materiale zawierającym uran ²³⁵U mogło dojść do reakcji łańcuchowej.

116.5

Oblicz liczbę jąder uranu ²³⁵U, które powinny ulec rozszczepieniu, aby uwolniona w reakcji energia wystarczyła do ogrzania 1 litra wody od temperatury 20^oC do 100^oC. Do obliczeń przyjmij ciepło właściwe wody równe 4200 J/kg·K.

Zadanie 117. (SR07)

117.1

Zapisz dwie cechy sił jądrowych.

117.2

Wykaż, że średnia gęstość materii jądrowej jest niezależna od liczby masowej. Wykorzystaj założenia podane poniżej.

1. Jądro atomowe można traktować jako kulę (objętość kuli V = π R³ ).
2. Empiryczny wzór określający promień jądra atomowego ma postać
   R = r ³  A ,    gdzie r = 1,2·10^-15 m, zaś A jest liczbą masową.
3. Masę jądra atomu można szacować jako iloczyn liczby masowej i masy neutronu.

117.3

Oszacuj promień gwiazdy neutronowej o masie 12,56·10²⁹ kg i średniej gęstości równej 3·10¹⁷ kg/m³

117.4

Masywna gwiazda w wyniku ewolucji utworzyła obiekt o masie 12,56·10²⁹ kg i promieniu 1 km. Oszacuj wartość drugiej prędkości kosmicznej dla tego obiektu. Oceń, czy ten obiekt może być „czarną dziurą”. Odpowiedź uzasadnij.

Zadanie 118. (SR08)

Amerykańska agencja kosmiczna (NASA) przygotowuje plany umożliwiające lądowanie na asteroidzie. NASA chce sprawdzić, czy jest możliwa zmiana kursu takiego ciała w przypadku, gdyby zmierzało ono w kierunku Ziemi. Naszej planecie może w 2029 roku zagrozić stosunkowo niewielka asteroida Apophis o masie 8·10 Astronomowie oceniają, że asteroida mija naszą planetę w niewielkiej odległości raz na 1500 lat. Podczas jednego obiegu wokół Słońca orbita Apophis dwukrotnie przecina się z orbitą Ziemi. Najbliższe zbliżenie do Ziemi nastąpi w piątek 13 kwietnia 2029 roku. Astronomowie szacują, że wartość prędkości asteroidy względem Ziemi w momencie potencjalnego zderzenia będzie wynosiła około 13 km/s.

Na podstawie:

http://neo.jpl.nasa.gov/news/news146.html

http://en.wikipedia.org/wiki/99942_Apophis

118.1  

Oszacuj wartość przyspieszenia grawitacyjnego na powierzchni asteroidy. W obliczeniach przyjmij, że asteroida jest jednorodną kulą.

118.2

Podaj, w którym położeniu (peryhelium czy aphelium) wartość prędkości obiegu asteroidy wokół Słońca jest najmniejsza. Odpowiedź uzasadnij, odwołując się do odpowiedniego prawa i podając jego treść.

118.3  

Oszacuj okres obiegu asteroidy wokół Słońca. Wynik podaj w dniach ziemskich.

Podczas obliczeń przyjmij, że asteroida porusza się po orbicie kołowej, rok ziemski trwa 365 dni, a średnia odległość Ziemi od Słońca jest równa 1 AU

118.4  

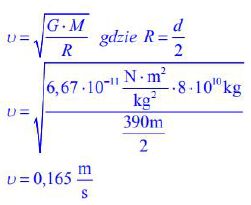
Wykaż, że wartość pierwszej prędkości kosmicznej dla asteroidy Apophis wynosi około 0,165 m/s.

118.5

Oblicz maksymalną energię, jaka może wydzielić się w momencie zderzenia asteroidy z powierzchnią Ziemi. Wyraź tę energię w megatonach (MT), przyjmując, że 1 MT ≈ 4·J.

Zadanie 119. (SR09)

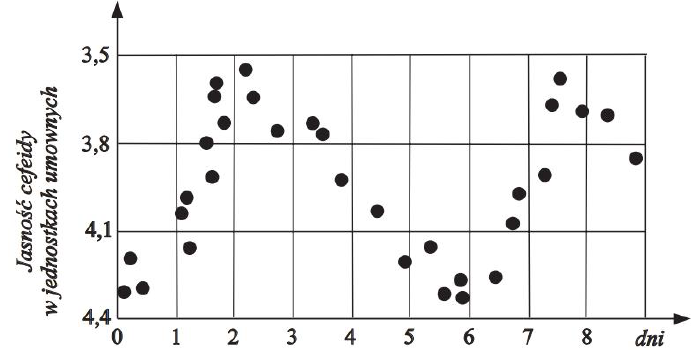
Cefeidy to regularnie zmieniające swoją jasność gwiazdy, nawet dziesięć tysięcy razy jaśniejsze od Słońca. Każda cefeida okresowo zmienia swoje rozmiary i temperaturę powierzchni. Własności cefeid wykorzystywane są do wyznaczania odległości do galaktyk, w których się znajdują. Swoją nazwę zawdzięczają gwieździe δ Cephei w gwiazdozbiorze Cefeusza. Jej rozmiary są kilkadziesiąt razy większe od Słońca, jej temperatura zmienia się od 6800 K w maksimum blasku do 5500 K w minimum, a moc jej promieniowania osiąga średnią wartość ok. 2000 razy większą niż Słońce.

W obliczeniach przyjmij, że moc promieniowania Słońca wynosi 3,82·10²⁶ W.

Poniżej przedstawiono diagram Hertzsprunga-Russella klasyfikujący gwiazdy, na którym zaznaczono obszary I, II, III, IV. Wykres dotyczy zadań 119.1 i 119.2.

Zadanie 119.1

Zapisz, w którym z zaznaczonych obszarów I, II, III, IV na diagramie Hertzsprunga-Russella znajduje się cefeida δ Cephei.

Zapisz nazwę gwiazd znajdujących się w obszarze I.

Odp.:

obszar III

białe karły

Zadanie 119.2

Oszacuj (w watach), w jakim przedziale zawiera się moc promieniowania gwiazd leżących na ciągu głównym.

Odp.:

Pmin ≈ 4·10W

Pmax ≈ 4·10W

Wykres przedstawia zmiany jasności w czasie dla pewnej cefeidy.

Zadanie 119.3

Oszacuj i zapisz okres zmian jasności tej cefeidy. Wykorzystaj dane zawarte na wykresie.

Odp.:

T ≈ 5,5 dnia

Zadanie 119.4

Moc promieniowania emitowanego z jednostki powierzchni gwiazdy zależy od temperatury jej powierzchni. Wyjaśnij, dlaczego cefeida δ Cephei emituje znacznie więcej energii niż Słońce, mimo podobnej temperatury powierzchni.

Odp.:

Cefeida ma większe rozmiary niż Słońce (promień, pole powierzchni) i dlatego

całkowita wypromieniowana moc jest większa..

Zadanie 119.5

Odległości do galaktyk, w których zidentyfikowano cefeidy, można wyznaczać, wykorzystując zależność pomiędzy okresem zmian jasności dla różnych cefeid i ich średnią mocą promieniowania. Na wykresie poniżej przedstawiono zależność między średnią mocą promieniowania a okresem zmian jasności.

Oblicz średnią moc promieniowania cefeidy o okresie zmian jasności 10 dni, korzystając z informacji zawartych w tekście wprowadzającym oraz na wykresie.

Odp.:

– odczytanie z wykresu mocy promieniowania cefeidy (ok. 4000 razy większa od mocy promieniowania Słońca)

– obliczenie mocy cefeidy P ≈ 1,5·10W

Zadanie 119.6

Strumień energii Φ (wyrażony w W/m²) padający prostopadle na jednostkową powierzchnię obliczamy  ze  wzoru: Φ =

, gdzie  P  jest  mocą  promieniowania  gwiazdy, a r jest odległością od gwiazdy. Na podstawie pomiarów ustalono, że średnia moc promieniowania pewnej cefeidy wynosi 12,56·10²⁸ W, a strumień energii docierający od tej cefeidy w pobliże Ziemi jest równy 1·10^–12 W/m².

Oblicz odległość tej cefeidy od Ziemi.

Odp.:

r =

r = 1·10m

Zadanie 119.7

Odległości wyznaczane opisaną powyżej metodą są bardzo duże i podaje się je w latach świetlnych lub w parsekach.

Wyraź odległość 10¹⁷ km w latach świetlnych.

Zadanie 120. (SR10)

GLAST (Gamma-ray Large Area Space Telescope) jest kosmicznym obserwatorium promieniowania gamma. Krąży po kołowej orbicie okołoziemskiej o promieniu 6920 km z prędkością około 7,6 km/s. Obserwatorium ma masę około 4300 kg i jest wyposażone w akumulatory oraz dwa panele baterii słonecznych o mocy około 3120 W.

Najważniejszym instrumentem satelity jest teleskop LAT, który może rejestrować co 10 µs pojedyncze fotony o energiach w zakresie od 20 MeV do 300 GeV. W jego wnętrzu znajdują się warstwy folii wolframowej, w której, w wyniku absorpcji fotonu, powstaje elektron i pozyton. Tory tych cząstek śledzone są za pomocą detektorów krzemowych. Cząstki oddają swoją energię w kalorymetrze, co umożliwia pomiar energii fotonu.

Na podstawie: „Świat Nauki” I/2008 oraz http://fermi.gsfc.nasa.gov/

120.1

Zapisz nazwy dwóch zasad zachowania, jakie są spełnione podczas rejestrowania fotonów.

120.2

Określ prawdziwość zdań, wpisując w odpowiednich miejscach wyraz: prawda lub fałsz.

Pomiar energii wydzielonej w kalorymetrze umożliwia wyznaczenie długości fali fotonu γ rejestrowanego w teleskopie LAT. ……………………………………

Teleskop LAT umożliwia śledzenie torów fotonów przy pomocy detektorów krzemowych. ……………………………………

120.3

Oblicz maksymalną liczbę fotonów, jaka może być zarejestrowana w ciągu jednej sekundy przez teleskop LAT.

120.4

Oblicz największą długość fali odpowiadającą fotonom rejestrowanych w teleskopie.

W obliczeniach przyjmij, że 1 eV = 1,6·10^–19 J.

 120.5

Oblicz okres obiegu satelity GLAST wokół Ziemi.

120.6

Zapisz nazwę urządzenia, które dostarcza energii elektrycznej do urządzeń satelity podczas przebywania satelity w cieniu Ziemi.

120.7

Wyjaśnij pojęcie czarna dziura.

Zadanie 121. (SR11)

Statek kosmiczny o masie 50 t po wyłączeniu silników przeleciał w pobliżu Marsa. W pewnej chwili t₀ statek przelatywał na wysokości 500 km nad powierzchnią planety. Masa Marsa wynosi 6,4·10²³ kg, a jego promień 3,4·10⁶ m.

121.1

Oblicz wartość przyspieszenia swobodnego spadku na powierzchni Marsa.

121.2

Oblicz prędkość ucieczki statku (minimalną prędkość początkową, jaką statek musiałby uzyskać na podanej wysokości 500 km, aby oddalić się z wyłączonymi silnikami na dowolnie dużą odległość od Marsa). Oblicz prędkość ruchu statku po orbicie kołowej na tej wysokości.

Jeśli początkowa prędkość statku miała wartość v₀ = 4·10³ m/s i była skierowana poziomo (prostopadle do prostej poprowadzonej do środka Marsa), to czy w miarę upływu czasu (t > t₀) odległość statku od planety będzie:

–    pozostawała stała,        –        rosła stale,

–    malała,        –        rosła, a potem malała?

Podkreśl właściwą spośród czterech powyższych możliwości i szczegółowo uzasadnij swój wybór.

Informacja do zadań 121.3 i 121.4

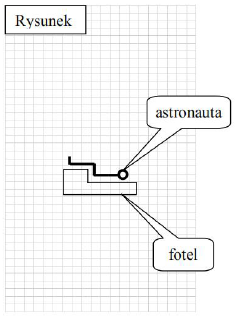
Od statku kosmicznego odłącza się lądownik z astronautą. W końcowej fazie lądowania (blisko powierzchni planety) lądownik porusza się pionowo z opóźnieniem równym 11 m/s².

121.3 

Narysuj, oznacz i opisz wszystkie siły działające na astronautę w końcowej fazie lądowania. Długości wektorów powinny przedstawiać zależności między ich wartościami. Narysuj siłę wypadkową (oznacz ją jako W), a jeśli jest ona równa zeru, to napisz, że W = 0.

121.4

Masa astronauty wynosi 80 kg, a natężenie pola grawitacyjnego Marsa ma wartość 3,7 N/kg. Oblicz wartość siły nacisku astronauty na fotel.

121.5

Na Marsie natężenie pola grawitacyjnego jest mniejsze, niż na Ziemi. Astronauci dokonują tam pomiaru okresu drgań pionowych ciężarka na sprężynie (wahadła sprężynowego) i okresu drgań ciężarka zawieszonego na nitce (wahadła matematycznego). Na Ziemi okresy drgań obydwu wahadeł były jednakowe. Czy na Marsie będą one także jednakowe, a jeśli nie, to dla którego wahadła okres drgań będzie dłuższy? Uzasadnij odpowiedź.

Zadanie 122. (SR11)

Sonda New Horizons została wystrzelona w 2006 roku w celu zbadania między innymi Jowisza i Plutona. Do zasilania sondy w energię elektryczną użyto generatora radioizotopowego z 11 kg preparatu promieniotwórczego zawierającego pluton ²³⁸Pu, którego okres połowicznego zaniku wynosi około 88 lat. Proces rozpadu promieniotwórczego ²³⁸Pu z emisją cząstek α powoduje znaczny wzrost temperatury preparatu. Wydzielane ciepło jest zamieniane na energię elektryczną przez specjalne urządzenie.

122.1

Uzupełnij schemat reakcji rozpadu plutonu.

122.2  

Uzupełnij schemat przemian energii zachodzących w generatorze radioizotopowym, wpisując w prostokątach, we właściwej kolejności, literę odpowiadającą danemu rodzajowi energii.

 A – energia elektryczna C – energia jądrowa

B – energia kinetyczna cząstek α D – ciepło

Informacja do zadań 122.3 i 122.5

Na początku wyprawy w 2006 roku generator dostarczał energię elektryczną o mocy 240 W. W miarę upływu lat moc dostarczana maleje: podczas przelotu koło Jowisza wynosiła 234 W, a szacuje się, że podczas przelotu koło Plutona (co ma nastąpić w roku 2015) moc spadnie do około 200 W.

122.3

Wyjaśnij, odwołując się do praw fizyki jądrowej, dlaczego moc generatora maleje z upływem czasu.

122.4  

Energia oddawana w formie ciepła przez preparat tylko w części może być przekształcana w energię elektryczną. Podaj nazwę prawa fizycznego, z którego wynika to stwierdzenie. Zapisz, dokąd i w jakiej formie zostaje przekazana pozostała część energii oddanej przez preparat (która nie została przekształcona w energię elektryczną).

122.5  

Sprawnością generatora nazywamy stosunek wytwarzanej energii elektrycznej do ciepła oddawanego przez preparat. Czy dla generatora sondy New Horizons z upływem lat sprawność rośnie, maleje, czy pozostaje stała? Podaj odpowiedź i uzasadnij ją na podstawie danych liczbowych wymienionych w informacjach na stronach 8 i 9 lub na podstawie praw fizyki.

122.6

Energia kinetyczna cząstki α emitowanej podczas rozpadu plutonu (Pu) wynosi 5,5 MeV, a prędkość cząstki, obliczona na podstawie wzoru E = , wynosi około 16300 km/s. Wybierz i podkreśl w tabeli prawidłowe zakończenie poniższego zdania.

Prędkość cząstki α emitowanej podczas rozpadu plutonu, obliczona z relatywistycznego wzoru na energię kinetyczną, w porównaniu z wynikiem obliczonym powyżej będzie

Uzasadnij dokonany wybór.

Zadanie 123. (SR12)

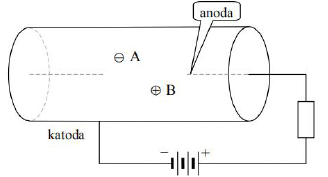
Detekcja promieniowania jądrowego jest możliwa dzięki zdolności cząstek promieniowania do jonizacji materii. Na tej zasadzie działa licznik Geigera–Müllera, który jest zbudowany ze szklanego cylindra i umieszczonej w nim rurki metalowej (katoda) oraz odizolowanego od niej cienkiego drutu znajdującego się na osi rurki (anoda). Cylinder wypełniony jest mieszaniną gazów pod niskim ciśnieniem. Atomy gazu ulegają jonizacji pod wpływem promieniowania jądrowego.

123.1  

Wyjaśnij krótko, na czym polega zjawisko jonizacji materii.

Informacja do zadań 123.2–123.3

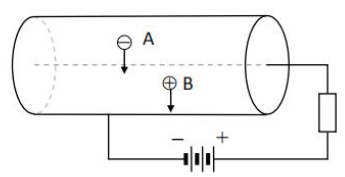
Rysunek przedstawia schemat budowy licznika. Wewnątrz licznika znajduje się elektron A oraz jon dodatni B. Wzajemne oddziaływanie cząstek A i B jest zaniedbywalnie małe.

123.2  

Na powyższym rysunku narysuj wektory sił elektrostatycznych działających na elektron A i jon B.

123.3

Elektron A i jon B znajdują się w tej samej odległości od anody. Która z tych cząstek zacznie się poruszać z większym przyspieszeniem, czy też przyspieszenia będą jednakowe? Napisz odpowiedź i ją uzasadnij.

123.4

Oblicz prędkość, jaką osiągnie początkowo spoczywający elektron przyspieszony w próżni napięciem 500 V. Pomiń efekty relatywistyczne.

Informacja do zadań 123.5–123.6

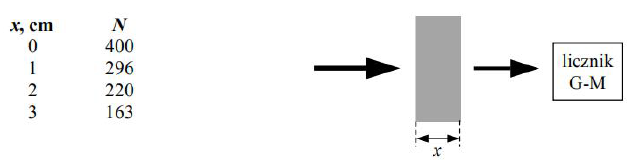
Za pomocą licznika Geigera-Müllera przeprowadzono pomiary natężenia promieniowania przechodzącego przez warstwę materiału pochłaniającego, przy ustalonym natężeniu promieniowania padającego, a różnej grubości materiału x. Wyniki (liczby impulsów na sekundę N) przedstawia tabela poniżej.

123.5

Wykonując odpowiednie obliczenia, ustal i napisz, czy poniższe stwierdzenie jest prawdziwe.

Liczba cząstek przechodzących przez materiał pochłaniający jest odwrotnie proporcjonalna do grubości x warstwy tego materiału.

123.6  

Oblicz stosunek liczby cząstek pochłoniętych do liczby cząstek przechodzących dla każdej kolejnej warstwy o ustalonej grubości 1 cm. Wyniki wpisz do poniższej tabeli.

Sformułuj wniosek wynikający z przeprowadzonych badań, podkreślając właściwe wyrażenie w nawiasie w poniższym zdaniu.

Zgodnie z wynikami doświadczenia, stosunek liczby cząstek pochłoniętych do liczby cząstek przechodzących był dla kolejnych warstw ( w przybliżeniu jednakowy / różny ).

Zadanie 124. (SR13)

Przypuszcza się, że Słońce powstało około 4,6 miliarda lat temu z obłoku gazu i pyłu nazywanego protogwiazdą. Po trwającym kilkadziesiąt milionów lat okresie kurczenia się obłoku Słońce stało się gwiazdą ciągu głównego. Zawartość wodoru w jądrze młodego Słońca wynosiła ok. 73%, a obecnie w wyniku ciągu reakcji termojądrowych spadła do 40%. Około 98% energii w Słońcu jest produkowane w cyklu p-p, w którym z czterech protonów powstaje jądro helu. Cykl ten jest wydajniejszy w temperaturach jądra gwiazdy rzędu 10 ⁷ K, natomiast w wyższych temperaturach (występujących w gwiazdach o masach większych niż Słońce) bardziej wydajny jest cykl CNO (węglowo-azotowy). Gdy zapasy wodoru się wyczerpią, co nastąpi po kolejnych 5 mld lat, Słońce zmieni się w czerwonego olbrzyma i po odrzuceniu zewnętrznych warstw tworzących mgławicę planetarną zacznie zapadać się pod własnym ciężarem, przeistaczając się w białego karła. Następnie przez wiele miliardów lat będzie nadal stygło, stając się brązowym, a później czarnym karłem.

124.1

Na wykresie Hertzsprunga-Russella przedstawiono ewolucję Słońca. Uzupełnij opis, wpisując w odpowiedniej kolejności właściwe nazwy etapów ewolucji, odpowiadające numerom na wykresie.

1. ……………………………………………..
2. ……………………………………………..
3. ……………………………………………..
4. ……………………………………………..
5. ……………………………………………..

124.2

Uzupełnij schematy reakcji jądrowych cyklu CNO.

124.3

Zawarty we wprowadzeniu do zadania opis cyklu p-p „z czterech protonów powstaje jądro helu” jest uproszczeniem, w którym pominięto pewne inne cząstki uczestniczące w tym cyklu.

a) Z czterech protonów nie może powstać tylko jądro helu, ani tylko jądro helu oraz energia w postaci kwantów promieniowania elektromagnetycznego lub neutrin. Napisz nazwę prawa fizycznego, które opisuje to ograniczenie.

b) Napisz nazwy dwóch różnych rodzajów lekkich cząstek, które oprócz jądra helu powstają z czterech protonów.

124.4

Odwołując się do budowy jąder atomowych, wyjaśnij:

a) dlaczego reakcje syntezy mogą zachodzić tylko w wysokich temperaturach.

b) dlaczego cykl CNO wymaga wyższych temperatur niż cykl p-p.

 124.5 (2 pkt)

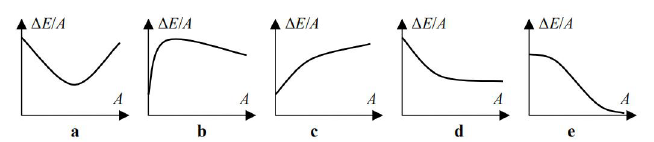
Iloraz energii wiązania jądra atomowego ΔE przez liczbę masową jądra A nazywamy właściwą energią wiązania jądra. Wybierz i podkreśl poprawny wykres przedstawiający schematycznie zależność właściwej energii wiązania od liczby masowej jąder atomowych.

Napisz, dlaczego energię jądrową możemy uzyskiwać w procesach rozpadu jąder ciężkich

Zadanie 125. (SR14)

Jądro neodymu Nd ulega rozpadowi α i przechodzi w jądro ceru Ce według schematu:

Masy jąder biorących udział w tej reakcji wynoszą odpowiednio:

mNd = 143,9099 u,

mCe = 139,9053 u,

mHe = 4,0026 u,

gdzie u jest jednostką masy atomowej.

125.1

Wykaż, że podczas powyższej reakcji wyzwala się energia równa 2,988·10J lub 1,867 MeV.

125.2

Oblicz energię kinetyczną jądra helu, które powstało w wyniku rozpadu spoczywającego jądra neodymu. Dana jest energia wyzwolona w rozpadzie jądra neodymu, równa 1,867 MeV. Prędkości jąder ceru i helu są znacznie mniejsze od prędkości światła. Należy uwzględnić fakt, że podczas rozpadu spełniona jest zasada zachowania pędu.

125.3  

W wyniku bombardowania jądra berylu Be cząstkami α można otrzymać jądro węgla C oraz jedną z cząstek elementarnych. Uzupełnij schemat opisanej reakcji.

125.4  

Przeprowadzenie reakcji opisanej w zadaniu 5.3 wymaga użycia cząstek α o dostatecznie dużej energii kinetycznej. Sprawdź, wykonując odpowiednie obliczenia, czy cząstka α o energii 4,8 MeV może pokonać odpychanie elektrostatyczne i zbliżyć się do jądra berylu na odległość porównywalną z promieniem tego jądra. Przyjmij, że jądro berylu pozostaje nieruchome, a jego promień wynosi 2,5·10

${}^{–15}$

m.

Zadanie 126. (SR14)

Przypuśćmy, że w pewnej galaktyce astronauci odkryli kulistą planetę, której masa jest dokładnie 3 razy mniejsza od masy Ziemi. Zmierzono promień planety 4,59·10m oraz okres drgań wahadła matematycznego o długości 1 m na równiku i na biegunie tej planety. Otrzymane wyniki pomiarów zamieszczono w środkowej kolumnie tabeli.

126.1

Wykaż, że podana wartość przyspieszenia swobodnego spadku na biegunie jest zgodna z zamieszczonymi wyżej informacjami o planecie.

126.2  

Wykaż, że podana wartość przyspieszenia swobodnego spadku na równiku jest zgodna z odpowiednim okresem wahadła.

126.3

Przyczyną różnicy między wartościami przyspieszenia swobodnego spadku na równiku i na biegunie jest obrót planety wokół własnej osi. Korzystając z wyników zamieszczonych w tabeli, oblicz okres obrotu tej planety.

126.4

Krótko po starcie z powierzchni planety statek kosmiczny uzyskał prędkość o wartości 8 km/s. Wykonując niezbędne obliczenia, sprawdź, czy ta prędkość wystarczy, aby statek mógł oddalić się od planety na dowolnie dużą odległość.

Zadanie 127. (SR15)

Pomysł pomiaru prędkości światła zrodził się już u Galileusza. Pierwszy laboratoryjny pomiar prędkości światła wykonał w 1849 r. francuski fizyk A. Fizeau. Schemat układu pomiarowego przedstawiono na rysunku poniżej. Światło wysłane przez źródło przechodziło przez zwierciadło półprzepuszczalne ZP, następnie przez szczelinę między zębami koła, odbijało się od zwierciadła odległego o L = 8633 m i – jeśli koło obracało się powoli – po odbiciu ponownie przechodziło przez tę samą szczelinę i po odbiciu od zwierciadła półprzepuszczalnego trafiało do obserwatora. Gdy stopniowo zwiększano częstotliwość obrotów koła, obraz ulegał zaciemnieniu (odbite światło trafiało na ząb koła), a następnie rozjaśnieniu (odbite światło trafiało w kolejną szczelinę).

127.1.  

Podaj główną przyczynę tego, że bezpośredni pomiar prędkości światła jest znacznie trudniejszy niż np. pomiar prędkości dźwięku w powietrzu.

127.2.  

Oblicz, jaką wartość prędkości światła otrzymał Fizeau, jeżeli pierwsze zaciemnienie wystąpiło, gdy koło obróciło się o jeden ząb (tzn. ząb przeszedł w położenie następnego zębu) w czasie 1,1∙10

${}^{–4}$

sekundy.

127.3.

Podaj dwie możliwe przyczyny niedokładności wyniku otrzymanego przez Fizeau.

127.4.  

Zanim uznano prędkość fali elektromagnetycznej w próżni za stałą znaną dokładnie, wykonywano pomiary tej wielkości dla różnych zakresów tych fal. Uzyskano wartości zamieszczone w tabeli.

Czy wyniki tych pomiarów są zgodne z hipotezą, że prędkość fali elektromagnetycznej w próżni nie zależy od jej częstotliwości? Napisz odpowiedź i jej krótkie uzasadnienie.

127.5.

W eksperymencie Michelsona–Morleya porównywano wartość prędkości światła biegnącego w próżni w różnych kierunkach. Wynik tego doświadczenia był jednym z najważniejszych w historii fizyki. Powołując się na obowiązującą obecnie teorię, napisz i uzasadnij, jaka powinna być różnica pomiędzy prędkością światła wysyłanego zgodnie i przeciwnie do zwrotu ruchu Ziemi. Laboratorium pomiarowe porusza się razem z Ziemią z prędkością jej ruchu orbitalnego, równą 30 km/s.

127.6.

Prędkość światła w próżni można wyznaczyć z teorii Maxwella. Sprawdź zgodność jednostek i na tej podstawie ustal, który ze wzorów jest poprawny.

127.7.  

W jaki sposób można w warunkach pracowni szkolnej wyznaczyć prędkość światła w wodzie? Przedstaw krótko zasadę pomiaru. Zakładamy, że prędkość światła w powietrzu jest znana.

Zadanie 128. (SR15)

Gdy gwiazda zużyje zapasy wodoru znajdujące się w jej jądrze, nadal może zachodzić proces syntezy termojądrowej w zewnętrznej helowej warstwie gwiazdy. Rezultatem tego procesu jest powstawanie jąder węgla w tzw. cyklu 3α. Połączenie dwóch cząstek α prowadzi do utworzenia jądra berylu, które zderza się z kolejną cząstką α, a w wyniku powstaje jądro węgla.

128.1.

Uzupełnij liczby atomowe i masowe w schemacie przemiany jąder helu (cząstek α) w jądro berylu.

128.2.  

Do połączenia dwóch cząstek α dochodzi w bardzo wysokiej temperaturze. W takich warunkach cząstki odpychające się siłami kulombowskimi zbliżają się na odległość około 1·10  m. Oblicz wartość siły odpychania dwóch cząstek α podczas syntezy termojądrowej.

128.3.

W sprzyjających warunkach, gdy jądro berylu zderzy się z następną cząstką α, zachodzi kolejna reakcja, w wyniku której powstają jądro węgla i dwa jednakowe fotony promieniowania elektromagnetycznego o łącznej energii 7,654 MeV. Oblicz długość fali promieniowania powstałego w reakcji i określ, czy zawiera się ono w przedziale widzialnym.

128.4.

Źródłem informacji o składzie chemicznym, a tym samym – o wieku gwiazd, jest analiza ich widma absorpcyjnego. Poniżej przedstawiono przykładowe widmo absorpcyjne z widocznymi ciemnymi liniami.

W poniższym tekście podkreśl właściwe słowa, tak aby powstał poprawny opis powstawania i obserwacji widm absorpcyjnych. Do obserwacji widm absorpcyjnych gwiazd stosuje się (mikroskopy / spektroskopy / lasery). W tych urządzeniach wskutek zjawiska (ugięcia / załamania / rozproszenia) światła gwiazdy na siatce dyfrakcyjnej i interferencji w obszarze za siatką dyfrakcyjną rozdzielane są różne barwy. Każdej linii absorpcyjnej odpowiada przeskok (fotonu / elektronu / protonu) z (niższego / wyższego) poziomu energetycznego na (niższy / wyższy). Podczas przeskoku pochłaniana jest energia równa (sumie / różnicy) energii poszczególnych poziomów energetycznych.

Zadanie 129. (NR15)

Znaczna część gwiazd, które widzimy na nocnym niebie, występuje w układach podwójnych. Gwiazdy fizycznie podwójne to układy złożone z dwóch gwiazd krążących dookoła wspólnego środka masy. Gołym okiem dostrzegane są zwykle jako gwiazdy pojedyncze. Załóżmy, że mamy do czynienia z układem dwóch gwiazd o różnych masach M i m, które krążą wokół wspólnego środka masy O po orbitach kołowych. Na rysunku obok przedstawiono 3 okręgi. Dwa spośród nich mogą być orbitami gwiazd tworzących układ podwójny. Na jednym z tych okręgów zaznaczono położenie gwiazdy o większej masie M.

129.1.

Zaznacz na odpowiednim okręgu i we właściwym miejscu oraz opisz literą m położenie gwiazdy o mniejszej masie.

129.2.

Dana jest odległość d między gwiazdami. Odległość środka masy układu od gwiazdy o masie M oznaczamy jako x. Rozmiary gwiazd należy pominąć.

Wyprowadź wzór wyrażający zależność x od d, M i m.

129.3.

Oceń prawdziwość poniższych zdań. Zaznacz P, jeśli zdanie jest prawdziwe, lub F – jeśli zdanie jest fałszywe.

1. Siły dośrodkowe FM oraz Fm działające na gwiazdy o masach M oraz m mają jednakowe wartości (FM = Fm). P F

2. Prędkości liniowe obu gwiazd względem środka masy układu mają tę samą wartość (vM = vm). P F

3. Częstotliwości, z jakimi gwiazdy obiegają swoje orbity, są równe (fM = fm). P F

Zadanie 130. (NR15)

Polon

${}^{210}$

Po jest źródłem promieniowania alfa, a czas połowicznego zaniku tego izotopu wynosi 139 dni. Próbka zawierająca jeden gram

${}^{210}$

Po wydziela ciepło o mocy około 140 W. Z tego względu polon jest używany jako źródło ciepła w satelitach i pojazdach kosmicznych do podgrzewania aparatury i wytwarzania prądu elektrycznego.

Na podstawie: http://www.rsc.org

130.1. 

Zaznacz właściwe dokończenie poniższego zdania.

Po upływie 2 lat moc grzewcza źródła, w którym zastosowano polon

${}^{210}$

Po , zmaleje i wyniesie

1. powyżej 1/5 mocy początkowej.
2. około 1/10 mocy początkowej.
3. około 1/25 mocy początkowej.
4. poniżej 1/30 mocy początkowej.

130.2.

Żadne urządzenie nie może przetwarzać ciepła w energię elektryczną ze sprawnością równą 100%.

Napisz nazwę prawa fizycznego, z którego wynika to stwierdzenie.

Zadanie 131. (NR15)

Katodę fotokomórki oświetlono światłem, którego długość fali jest równa 370 nm. Moc promieniowania padającego na powierzchnię katody jest równa 6,0 μW.

131.1.

W poniższej tabeli zamieszczono wybrane metale, dla których podano wartości pracy wyjścia.

Na podstawie: H. Stöcker, Nowoczesne kompendium fizyki, Warszawa 2010.

Wybierz wszystkie metale, z których można wykonać katodę, aby móc obserwować zjawisko fotoelektryczne dla światła opisanego wyżej. Wybór uzasadnij, wykonując odpowiednie obliczenia.

Informacja do zadań 131.2. i 131.3.

Fotokomórkę połączono szeregowo z amperomierzem i całość zasilano napięciem, którego wzrost skutkował wzrostem natężenia prądu płynącego przez fotokomórkę do wartości 0,5 μA (wykres obok).

131.2. 

Wyjaśnij, dlaczego natężenie prądu nie przekracza pewnej wartości.

131.3.

a) Oblicz liczbę fotonów padających na katodę w ciągu 1 sekundy.

b) Oblicz liczbę elektronów przepływających w ciągu 1 sekundy w obwodzie, w którym natężenie prądu wynosi 0,5 μA.

c) Oszacuj, jaka część liczby fotonów padających na katodę spowodowała wybicie elektronów w opisanej fotokomórce.

Zadanie 132. (NR15)

Podkreśl właściwe określenia, tak aby powstały zdania prawdziwe.

• Przypuszcza się, że Słońce powstało około 4,6 miliarda lat temu. Głównym źródłem energii Słońca są reakcje (łączenia / rozpadu) jąder (lekkich / ciężkich).

• Układ Słoneczny znajduje się (w centrum Galaktyki / około 30 tys. lat świetlnych od centrum Galaktyki).
• W obecnej chwili Wszechświat (powoli kurczy się / zachowuje stałe rozmiary / stale się rozszerza).