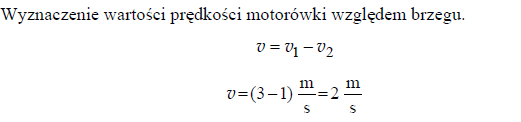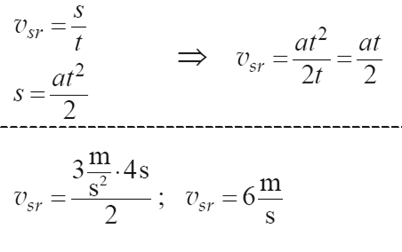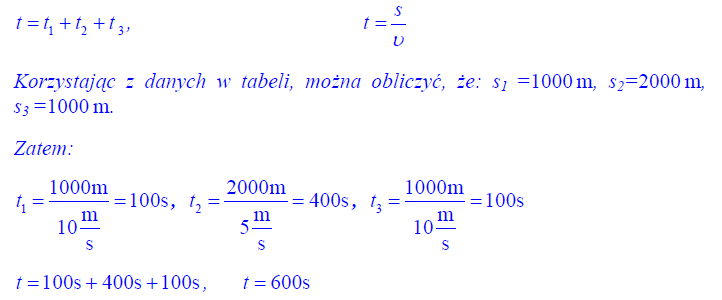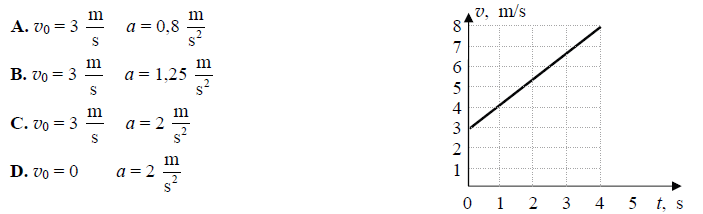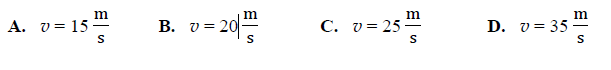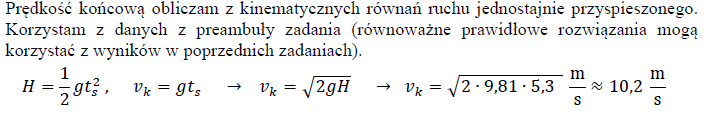Zadania maturalne z Fizyki
Temat: Kinematyka
Zadania pochodzą z oficjalnych arkuszy maturalnych CKE, które służyły przeprowadzaniu majowych egzaminów. Czteroznakowy kod zapisany przy każdym zadaniu wskazuje na jego pochodzenie: S/N – „stara”/”nowa” formuła; P/R – poziom podstawowy/rozszerzony; np. 08 – rok 2008.
Zbiór zadań maturalnych w formie arkuszy, możesz pobrać >> TUTAJ <<.
Zadanie 1. (SP05)
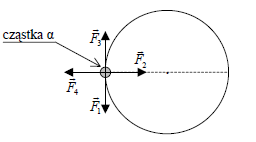
Cząstka α porusza się po okręgu (rys.) z prędkością o stałej wartości i zmiennym kierunku.
Siłę zmieniającą prędkość przedstawia wektor
Zadanie 2. (SP05)
Po rzece, której nurt ma prędkość 1 m/s, płynie pod prąd motorówka. Wartość prędkości motorówki względem wody wynosi 3 m/s. Oblicz, ile sekund będzie trwał rejs motorówką między przystaniami odległymi od siebie o 2000 m.
Zadanie 3. (SP06)
Tomek wchodzi po schodach z parteru na piętro. Różnica wysokości między parterem a piętrem wynosi 3 m, a łączna długość dwóch odcinków schodów jest równa 6 m. Wektor całkowitego przemieszczenia Tomka ma wartość
- 3 m
- 4,5 m
- 6 m
- 9 m
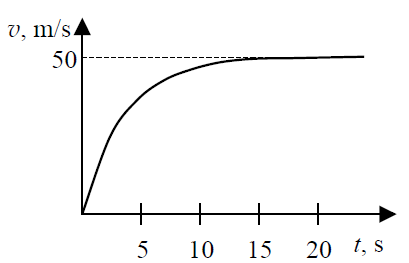
Zadanie 4. (SP06)
Wykres przedstawia zależność wartości prędkości od czasu dla ciała o masie 10 kg, spadającego w powietrzu z dużej wysokości. Analizując wykres można stwierdzić, że podczas pierwszych 15 sekund ruchu wartość siły oporu
- jest stała i wynosi 50 N.
- jest stała i wynosi 100 N.
- rośnie do maksymalnej wartości 50 N.
- rośnie do maksymalnej wartości 100 N.
Zadanie 5. (SP07)
Dwaj rowerzyści poruszając się w kierunkach wzajemnie prostopadłych oddalają się od siebie z prędkością względną o wartości 5 m/s. Wartość prędkości jednego z nich jest równa 4 m/s, natomiast wartość prędkości drugiego rowerzysty wynosi
- 1 m/s.
- 3 m/s.
- 4,5 m/s.
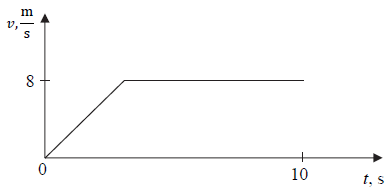
- 9 m/s.
Zadanie 6. (SP07)
Samochód rusza z miejsca ruchem jednostajnie przyspieszonym z przyspieszeniem o wartości 3 m/s2 i porusza się po prostoliniowym, poziomym odcinku autostrady. Oblicz wartość prędkości średniej samochodu po pierwszych czterech sekundach ruchu.
Zadanie 7. (SP08)
Rowerzysta pokonuje drogę o długości 4 km w trzech etapach, o których informacje przedstawiono w tabeli. Przez d oznaczono całą długość drogi przebytej przez rowerzystę.
Oblicz całkowity czas jazdy rowerzysty.
Zadanie 8. (SP09)
Samochód porusza się po prostoliniowym odcinku autostrady. Drogę przebytą przez samochód opisuje równanie: s = 15 t + 1,5 t2 (w układzie SI z pominięciem jednostek).
Wartości prędkości początkowej i przyspieszenia samochodu wynoszą odpowiednio
Zadanie 9. (SP09)
Małą kulkę przymocowaną do nici wprawiono w ruch jednostajny po okręgu w płaszczyźnie poziomej. Przyspieszenie dośrodkowe kulki jest związane ze zmianą
- wartości prędkości liniowej.
- kierunku prędkości liniowej.
- wartości prędkości kątowej.
- kierunku prędkości kątowej.
Zadanie 10. (SP09)
Piłka uderza o podłogę z prędkością o wartości 2 m/s skierowaną prostopadle do podłogi i odbija się od niej z prędkością o wartości 1,5 m/s. Bezwzględna wartość zmiany prędkości piłki podczas odbicia wynosi
- 0 m/s.
- 0,5 m/s.
- 2,5 m/s.
- 3,5 m/s.
Zadanie 11. (SP10)
Po przelocie samolotu powstaje smuga kondensacyjna spalin, tworząc na niebie ślad (rysunek). Ślad ten przedstawia
- tor.
- drogę.
- prędkość.
- przemieszczenie.
Zadanie 12. (SP12)
Sokół leci po linii prostej z prędkością 25 m/s, goniąc gołębia, który porusza się po tej samej prostej z prędkością 20 m/s. Jeśli początkowa odległość między ptakami wynosiła 0,5 km, to sokół dogoni gołębia w czasie
- 0,1 s.
- 11,1 s.
- 20 s.
- 100 s.
Zadanie 13. (SP12)
Na podstawie podanego wykresu zależności prędkości od czasu można stwierdzić, że prędkość początkowa v0 i przyspieszenie a ciała są równe odpowiednio
Zadanie 14. (SP12)
Rowery tego typu były produkowane w 70-tych i 80-tych latach XIX wieku. Przyjmijmy, że duże koło przednie miało średnicę 150 cm, a małe tylne – 50 cm. Cyklista jadąc szybko, wykonywał jeden obrót pedałami (sztywno połączonymi z kołem przednim) w ciągu sekundy.
- a) Podaj liczbę obrotów małego koła w ciągu sekundy.
- b) Oblicz wartość prędkości, z jaką poruszał się bicykl.
Liczba obrotów małego koła w ciągu sekundy jest równa 3, a wartość prędkości bicykla wynosi v = 2π · 75 cm / 1 s = 4,71 m/s.
Zadanie 15. (SP13)
Kamień rzucono pionowo w górę z prędkością 5 m/s. Jeśli pominiemy opór powietrza, a wartość przyspieszenia ziemskiego przyjmiemy równą 10 m/s2, to prawdą jest, że
- kamień wznosi się o 5 m w ciągu każdej sekundy.
- kamień osiągnie maksymalną wysokość 5 m.
- prędkość kamienia zmaleje o 5 m/s w ciągu pierwszej sekundy.
- czas lotu kamienia w górę będzie równy 0,5 s.
Zadanie 16. (SP13)
Pociąg o długości 260 m, jadący z prędkością 30 m/s, mija się z pociągiem o długości 180 m, jadącym w przeciwną stronę. Czas mijania pociągów, liczony od momentu minięcia się ich przodów do momentu minięcia się ich końców, wynosił 8,3 s. Oblicz prędkość drugiego pociągu.
Zadanie 17. (SP14)
Pasażer siedzący w przedziale pociągu poruszającego się z prędkością o wartości 10 m/s widzi przez 6 s pociąg jadący w przeciwną stronę. Jeśli długość mijanego pociągu jest równa 150 m, to wartość jego prędkości wynosi
Zadanie 18. (NP15)
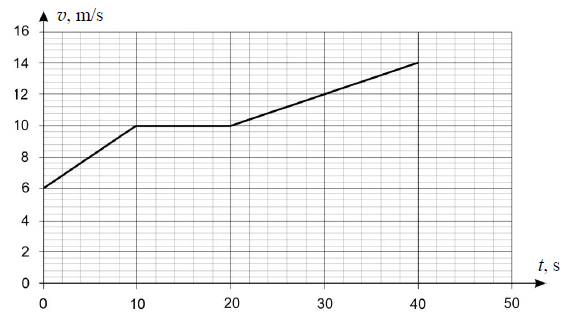
Wykres przedstawia zależność prędkości od czasu dla kolarza podczas trzech etapów jego ruchu.
a) Prędkość średnia kolarza w czasie pierwszych 20 sekund ruchu miała wartość
A. 6 m/s
B. 8 m/s
C. 9 m/s
D. 10 m/s
b)Wartość przyspieszenia kolarza w przedziale czasu od t = 20 s do t = 40 s wynosiła
A. 0,4 m/s2
B. 0,3 m/s2
C. 0,2 m/s2
D. 0,1 m/s2
a):
C
b):
C
Zadanie 19. (NP16)
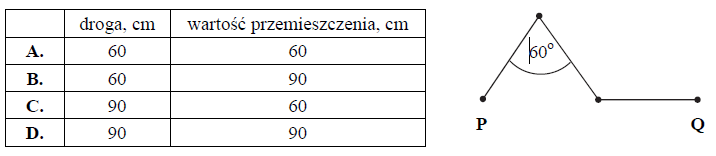
Model samochodziku porusza się z punktu P do Q po poziomej powierzchni po torze przedstawionym na rysunku. Każdy z odcinków toru ma długość 30 cm. Droga przebyta przez samochodzik i wartość jego przemieszczenia wynoszą odpowiednio
Zadanie 20. (NP16)
Samochód porusza się po rondzie z prędkością o wartości 20 km/h. Jeżeli wartość jego prędkości wzrośnie o 20 km/h i samochód nie zmieni pasa ruchu, to wartość przyspieszenia dośrodkowego samochodu
- zmaleje dwukrotnie.
- zmaleje czterokrotnie.
- wzrośnie dwukrotnie.
- wzrośnie czterokrotnie.
Zadanie 21. (NP16)
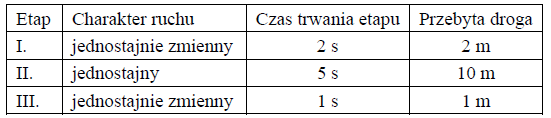
Dźwig budowlany podnosił pionowo betonowy element. W tabeli przedstawiono czasy i przebyte drogi w trzech kolejnych etapach podnoszenia. W chwili początkowej element się nie poruszał.
Narysuj wykres zależności v(t), gdzie v jest wartością prędkości elementu, a t – czasem.
Zadanie 22. (NP17)
Woda w rzece płynie z prędkością 2 m/s względem brzegu. Po pokładzie statku płynącego pod prąd z prędkością 3 m/s względem wody biegnie marynarz, który pozostaje w spoczynku względem brzegu. Prędkość marynarza względem pokładu statku jest równa
Zadanie 23. (NP17)
Podczas zabawy w skateparku chłopiec zjeżdża na deskorolce po rampie, której przekrój poprzeczny przypomina kształtem dwie ćwiartki okręgu połączone poziomym odcinkiem (patrz rysunek). W czasie zjazdu z rampy od punktu A do punktu B wartości prędkości oraz przyśpieszenia dośrodkowego chłopca zmieniają się w ten sposób, że
- prędkość i przyśpieszenie dośrodkowe rosną.
- prędkość rośnie, a przyśpieszenie dośrodkowe maleje.
- prędkość i przyśpieszenie dośrodkowe maleją.
- prędkość maleje, a przyśpieszenie dośrodkowe rośnie.
Zadanie 24. (NP17)
Punkt materialny porusza się po linii prostej: przebywa drogę 67 m w czasie 10 s. Na wykresie przedstawiono zależność wartości prędkości punktu od czasu.
Oblicz czas, w którym punkt materialny poruszał się ruchem jednostajnie przyśpieszonym, a następnie oblicz wartość przyśpieszenia, z jakim poruszał się ten punkt do momentu osiągnięcia maksymalnej prędkości.
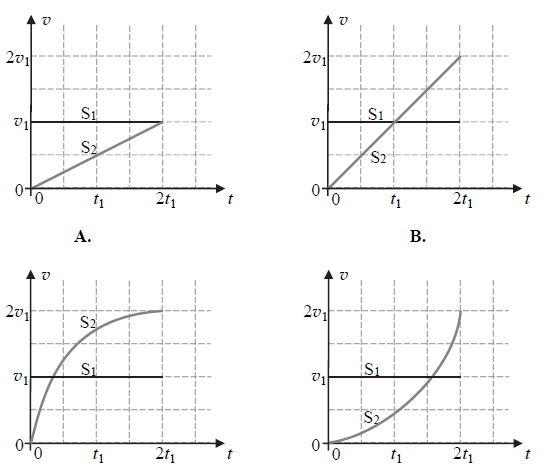
Zadanie 25. (NP18)
Samochód S1 jedzie ze stałą prędkością wzdłuż prostoliniowego odcinka trasy i w pewnej chwili wymija nieruchomo stojący samochód S2. W momencie, gdy samochód S1 wymija S2, ten rusza ze stałym przyspieszeniem i po pewnym czasie dogania samochód S1. Tory ruchu obu samochodów są równoległe. Poprawną zależność prędkości od czasu (od chwili, gdy S2 ruszył, do momentu, gdy dogonił S1) dla każdego z samochodów przedstawia wykres
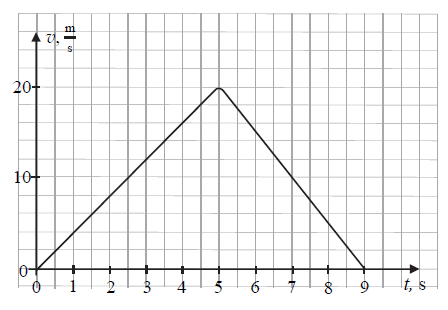
Zadanie 26. (NP18)
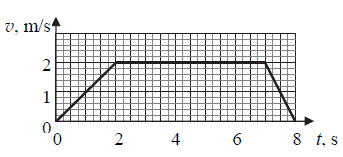
Motocykl ruszył ze skrzyżowania i po 9 sekundach zatrzymał się przed następnym skrzyżowaniem. Na wykresie obok przedstawiono zależność wartości prędkości motocykla od czasu trwania tego ruchu. Przejazd od jednego do drugiego skrzyżowania odbywał się po prostym, poziomym odcinku jezdni, a kierujący pojazdem ma masę 90 kg.
Oblicz drogę, jaką przebył motocyklista w opisanym ruchu pomiędzy skrzyżowaniami.
Zadanie 27. (NP19)
Pociąg porusza się ruchem jednostajnym prostoliniowym względem ziemi z prędkością o wartości 25 m/s. Wzdłuż wagonu pociągu idzie pasażer z prędkością o wartości około 1,5 m/s względem pociągu. Pasażer porusza się w tę samą stronę co pociąg. Droga, jaką pokona pasażer względem ziemi w czasie 5 s, wynosi około
- 125 m
- 117,5 m
- 7,5 m
- 132,5 m
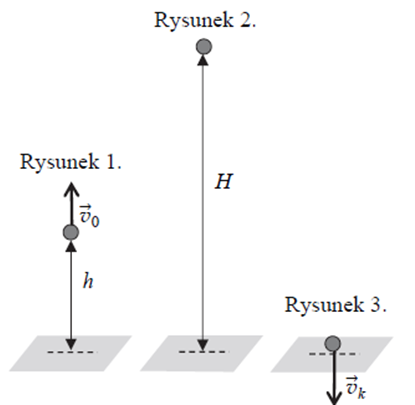
Zadanie 28. (NP19)
Podczas gry chłopiec podrzucił piłkę. W momencie wyrzutu piłka znajdowała się na wysokości h = 1,96 m nad powierzchnią ziemi. Jej prędkość V0 była skierowana pionowo w górę, a wartość tej prędkości była równa 8,1 m/s. Piłka wznosiła się na wysokość H=5,3 m ponad ziemię, po czym swobodnie opadła na ziemię.
W zadaniu pomiń opory ruchy oraz wykorzystaj wartość przyspieszenia ziemskiego równą g=9,81 m/s2. Rysunek 1. jest ilustracją opisanego rzutu w chwili początkowej, rysunek 2. – w chwili, gdy piłka osiągnęła wysokość maksymalną, a rysunek 3. przedstawia moment tuż przed uderzeniem piłki o ziemie.
a) Wykonaj odpowiednie obliczenia i wykaż, że w opisanym rzucie pionowym piłka wzniosła się na wysokość H=5,3 m ponad ziemię.
b) Oblicz całkowity czas ruchu piłki w opisanym rzucie: od momentu wyrzucenia aż do chwili uderzenia piłki o ziemię.
c) Wykonaj odpowiednie obliczenia i wykaż, że wartość vk prędkości piłki tuż przed uderzeniem o ziemię jest równa około 10,2 m/s.
a):
b):
c):
Zadanie 29. (SR09)
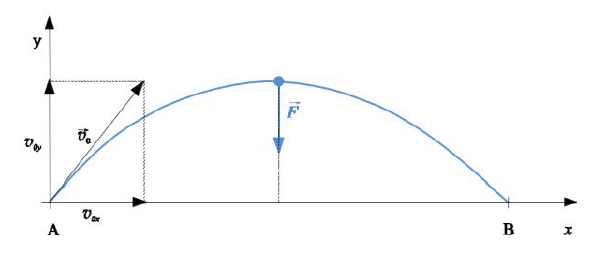
Podczas treningu zawodnik stoją czy w punkcie A kopnął piłkę pod kątem α do poziomu tak, że upadła na ziemię w punkcie B w odległości 38,4 m od niego. Składowe wektora prędkości
mają wartości: v= 12 m/s i v= 16 m/s.
Zasięg rzutu w takich warunkach można obliczyć ze wzoru
Rozwiązując zadania, przyjmij wartość przyspieszenia ziemskiego równą 10 m/s2, a opór powietrza pomiń.
29.1
Na rysunku powyżej naszkicuj tor ruchu piłki kopniętej przez zawodnika oraz zaznacz wektor siły działającej na piłkę w najwyższym punkcie toru.
29.2
Oblicz czas lotu piłki z punktu A do punktu B.
29.3
Oblicz wartość prędkości początkowej, jaką zawodnik nadał piłce.
29.4
Oblicz maksymalną wysokość, jaką osiągnęła piłka.
29.5
Inny zawodnik kopnął piłkę tak, że podczas lotu współrzędne jej położenia zmieniały się w czasie według wzorów: x(t) = 5t oraz y(t) = 6t – 5t2 (w układzie SI z pominięciem jednostek).
Wyprowadź równanie ruchu piłki, czyli zależność y(x).
29.6
Irlandzkiemu zawodnikowi Stevenowi Reidowi udało się nadać kopniętej piłce prędkość o rekordowej wartości 52,5 m/s.
Oblicz, jaki byłby maksymalny zasięg dla piłki, która po kopnięciu zaczyna poruszać się z wyżej podaną wartością prędkości przy zaniedbaniu oporów ruchu.
29.1
29.2
t = 3,2 s
29.3
vo = 20 m/s
29.4
Z zasady zachowania energii lub równań ruchu.
h = 12,8 m
29.5
t=
y = 1,2 x − 0,2 x 2 ( y = −0,2 x 2 + 1,2 x )
29.6
z max ≈ 276 m
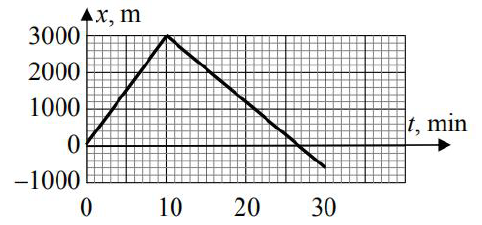
Zadanie 30. (SR13)
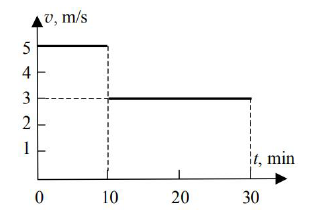
Na wykresie przedstawiono zależność wartości prędkości motorówki względem brzegu od czasu. Motorówka pływała wzdłuż prostoliniowego brzegu rzeki z prądem i pod prąd. Przez cały czas silnik motorówki pracował z pełną mocą i wartość prędkości motorówki względem wody była stała. Prędkość wody w rzece także była stała i mniejsza od prędkości motorówki względem wody.
30.1
Oblicz drogę, jaką przebyła motorówka w czasie 30 minut ruchu.
30.2
Oblicz wartość prędkości motorówki względem wody.
30.3
Narysuj wykres zależności położenia x motorówki od czasu t. Przyjmij, że oś x jest zwrócona zgodnie z nurtem rzeki, a ruch rozpoczyna się w punkcie x0 = 0.
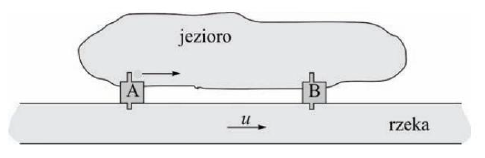
30.4
Z przystani A wyruszają jednocześnie z jednakową i stałą prędkością v względem wody dwie motorówki. Jedna płynie po jeziorze, a druga – po rzece płynącej z A do B z prędkością u względem brzegu. Po dopłynięciu do przystani B motorówki zawracają. Ustal, która motorówka wcześniej powróci do przystani A. Odpowiedź uzasadnij, zapisując odpowiednie zależności.
30.1
Mnożąc prędkość 5 m/s przez czas 10 minut = 600 s, otrzymujemy drogę 3000 m, a mnożąc 3 m/s przez 20 minut, otrzymujemy 3600 m. Całkowita droga wynosi 6600 m.
30.2
Prędkość motorówki płynącej z prądem jest równa sumie prędkości motorówki względem wody v i prędkości nurtu rzeki u: 5 m/s = v + u. Prędkość motorówki płynącej pod prąd jest równa różnicy tych prędkości: 3 m/s = v – u. Po wyeliminowaniu u znajdujemy v = 4 m/s.
30.3
30.4
Czas ruchu motorówki po jeziorze jest opisany wzorem 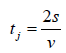
Widzimy, że trz > tj, czyli wcześniej powróci motorówka płynąca po jeziorze.
Zadanie 31. (NR15)
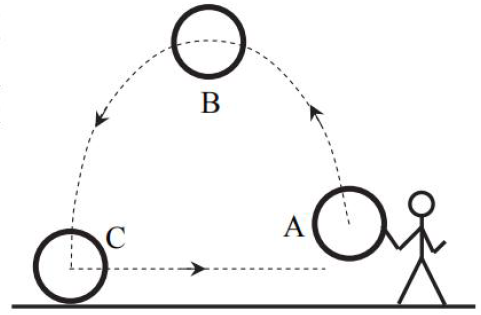
Gimnastyczka rzuciła ukośnie w górę plastikową obręcz, nadając jej jednocześnie ruch obrotowy w płaszczyźnie pionowej. Obręcz po upadku na podłoże powróciła do gimnastyczki. Rysunek przedstawia kolejne położenia A, B i C obręczy.
31.1.
W położeniu B narysuj symbol lub wskazujący, w którą stronę powinna obracać się obręcz, aby po upadku mogła wrócić do gimnastyczki.
31.2.
Wybierz spośród podanych i zaznacz właściwe dokończenie poniższego zdania.
Jeśli można pominąć opór powietrza, to prędkość ruchu obrotowego obręczy jest
- największa tuż po wyrzuceniu obręczy.
- największa, gdy obręcz jest w najwyższym punkcie B.
- największa tuż po wyrzuceniu i tuż przed upadkiem na podłoże.
- taka sama od momentu wyrzucenia aż do upadku.
31.3.
Obręcz tocząca się z położenia C do gimnastyczki nie przewraca się, pomimo że styka się z podłożem praktycznie w jednym punkcie.
Napisz nazwę prawa fizycznego, które wyjaśnia, dlaczego obręcz się nie przewraca.
31.4.
Wybierz spośród podanych i zaznacz właściwe dokończenie poniższego zdania.
Powrót obręczy z położenia C do gimnastyczki jest skutkiem działania siły
- grawitacji.
- tarcia.
- odśrodkowej.
- oporu powietrza.
31.1
narysowanie przy położeniu B symbolu .
31.2
D
31.3
Jest to zasada zachowania momentu pędu (lub zasada zachowania krętu).
31.4
B