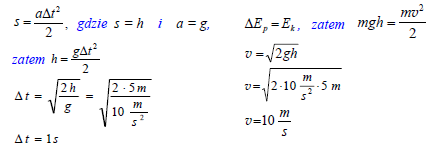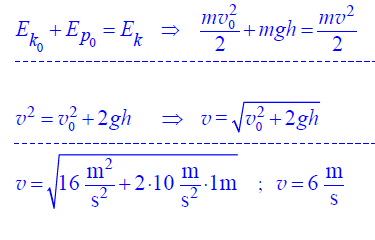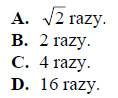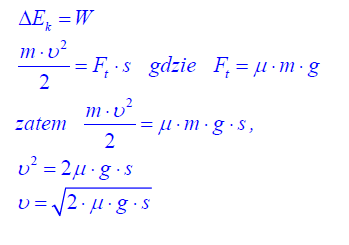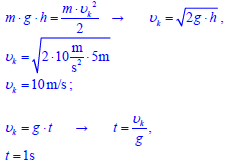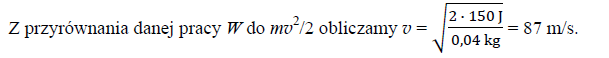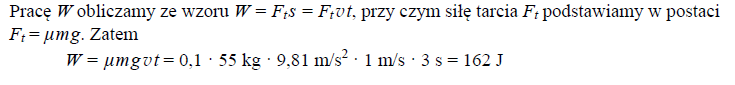Zadania maturalne z Fizyki

Temat: Moc i praca

Zadania pochodzą z oficjalnych arkuszy maturalnych CKE, które służyły przeprowadzaniu majowych egzaminów. Czteroznakowy kod zapisany przy każdym zadaniu wskazuje na jego pochodzenie: S/N – „stara”/”nowa” formuła; P/R – poziom podstawowy/rozszerzony; np. 08 – rok 2008.

Zbiór zadań maturalnych w formie arkuszy, możesz pobrać >> TUTAJ <<.

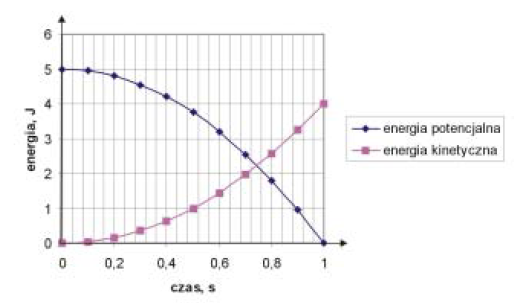
Zadanie 1. (SP05)

Z balkonu znajdującego się na wysokości 5 m nad ziemią dziecko upuściło misia (bez prędkości początkowej). Na poniższym wykresie przedstawiono zależność energii potencjalnej i kinetycznej spadającego misia od czasu.

Na podstawie wykresu określ, które z poniższych stwierdzeń jest nieprawdziwe.

1. Czas spadania misia był równy 1 s.
2. Masa spadającego misia wynosi 0,1 kg.
3. Podczas spadania misia działają siły oporu.
4. Miś uderzył w ziemię z prędkością 12 m/s.

Zadanie 2. (SP06)

Piłkę o masie 1 kg upuszczono swobodnie z wysokości 1 m. Po odbiciu od podłoża piłka wzniosła się na maksymalną wysokość 50 cm. W wyniku zderzenia z podłożem i w trakcie ruchu piłka straciła energię o wartości około

1. 1 J
2. 2 J
3. 5 J
4. 10 J

Zadanie 3. (SP06)

Z krawędzi dachu znajdującego się na wysokości 5 m nad powierzchnią chodnika spadają krople deszczu.

3.1

Wykaż, że czas spadania kropli wynosi 1 s, a jej prędkość końcowa jest równa 10 m/s.

W obliczeniach pomiń opór powietrza oraz przyjmij, że wartość przyspieszenia ziemskiego jest równa 10 m/s2.

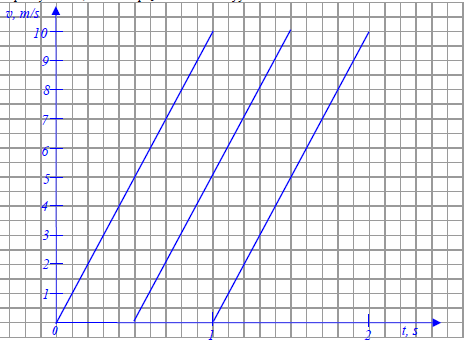
3.2

Uczeń, obserwując spadające krople ustalił, że uderzają one w chodnik w jednakowych odstępach czasu co 0,5 sekundy. Przedstaw na wykresie zależność wartości prędkości od czasu dla co najmniej 3 kolejnych kropli. Wykonując wykres przyjmij, że czas spadania kropli wynosi 1 s, a wartość prędkości końcowej jest równa 10 m/s.

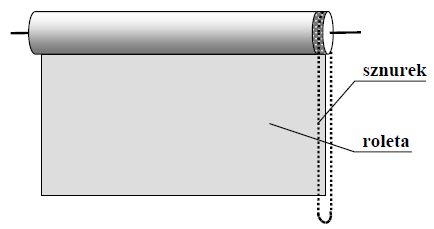
Zadanie 4. (SP06)

Roleta okienna zbudowana jest z wałka, na którym nawijane jest płótno zasłaniające okno (rys). Roletę można podnosić i opuszczać za pomocą sznurka obracającego wałek.

Oblicz pracę, jaką należy wykonać, aby podnieść rozwiniętą roletę, nawijając całkowicie płótno na wałek. Długość płótna całkowicie rozwiniętej rolety wynosi 2 m, a jego masa 2 kg.

Zadanie 5. (SP06)

Stalowy pocisk, lecący z prędkością o wartości 300 m/s wbił się w hałdę piasku i ugrzązł w niej.

Wyjaśnij krótko, na co została zużyta reszta energii kinetycznej pocisku.

Zadanie 6. (SP07)

Rozciągnięcie sprężyny o 1 cm z położenia równowagi wymaga wykonania pracy 2 J. Rozciągnięcie tej samej sprężyny o 3 cm, również z położenia równowagi, wymaga wykonania pracy

1. 6 J.
2. 12 J.
3. 18 J.
4. 24 J.

Zadanie 7. (SP07)

Gimnastyczka wyrzuciła pionowo w górę piłkę z prędkością o wartości 4 m/s. Piłka w momencie wyrzucania znajdowała się na wysokości 1 m licząc od podłogi. Oblicz wartość prędkości, z jaką piłka uderzy o podłogę. Załóż, że na piłkę nie działa siła oporu.

Zadanie 8. (SP08)

Jeżeli podczas ruchu samochodu, na prostoliniowym odcinku autostrady energia kinetyczna samochodu wzrosła 4 razy, to wartość prędkości samochodu wzrosła

Zadanie 9. (SP08)

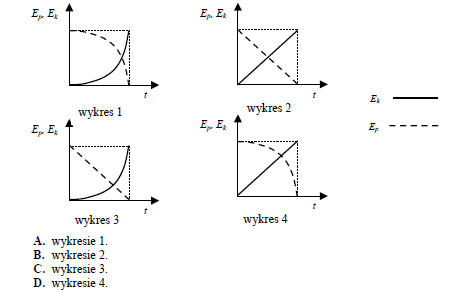
Zależność energii potencjalnej i kinetycznej od czasu podczas swobodnego spadania ciała z pewnej wysokości poprawnie przedstawiono na

Zadanie 10. (SP08)

Wykaż, wykorzystując pojęcia energii i pracy, że znając współczynnik tarcia i drogę podczas hamowania do całkowitego zatrzymania pojazdu, można wyznaczyć prędkość początkową pojazdu, który porusza się po poziomej prostej drodze. Przyjmij, że samochód hamuje ruchem jednostajnie opóźnionym, a wartość siły hamowania jest stała.

Zadanie 11. (SP08)

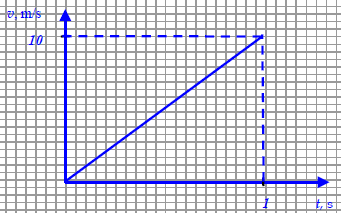
Fragment balkonu o masie 0,5 kg oderwał się i spadł z wysokości 5 m. W obliczeniach przyjmij, że wartość przyspieszenia ziemskiego wynosi 10 m/s2.

11.1

Narysuj wykres zależności wartości prędkości od czasu spadania. Wykonaj konieczne obliczenia, pomijając opory ruchu. Na wykresie zaznacz odpowiednie wartości liczbowe.

Zadanie 12. (SP11)

Na którym z poniższych wykresów zakreskowane pole jest równe wykonanej pracy?

A. Tylko na 1 B. Tylko na 2 C. Tylko na 1 i 2 D. Tylko na 1 i 3

Zadanie 13. (SP11)

Ciało na powierzchni Księżyca ma energię potencjalną grawitacji równą zero, a na wysokości 12 m ma energię potencjalną grawitacji równą 600 J. Podczas spadku swobodnego z wysokości 12 m, na wysokości 4 m energia kinetyczna tego ciała ma wartość

1. równą 600 J.
2. równą 400 J.
3. równą 200 J.
4. równą 100 J.

Zadanie 14. (SP12)

Pocisk o masie 10 g lecący poziomo z prędkością 600 m/s wpada do pudła z piaskiem o masie 5 kg i grzęźnie w nim. Pudło początkowo spoczywało na poziomym podłożu. Współczynnik tarcia pudła o podłoże wynosi 0,3.

Uzupełnij zdanie, wpisując większa od, mniejsza od lub równa.

Energia kinetyczna pudła wraz z pociskiem tuż po jego ugrzęźnięciu jest ……………………….. początkowej energii kinetycznej pocisku. Uzasadnij swój wybór.

Zadanie 15. (SP13)

15.1

Naciągamy cięciwę łuku i wypuszczamy strzałę. Wpisz w pustych polach nazwy rodzajów energii, tak aby diagram poprawnie opisywał przemiany energii w tym procesie

15.2

Praca wykonana przy napinaniu łuku wynosiła 150 J. Oblicz wartość prędkości strzały o masie 40 g wystrzelonej z tego łuku. Pomiń energię związaną z ruchem części samego łuku (np. cięciwy) oraz inne straty energii mechanicznej.

Zadanie 16. (SP14)

Niewielka piłka o masie 400 g spada z wysokości 10 m nad ziemią. Przyjmujemy, że powierzchnia ziemi jest poziomem odniesienia.

16.1

Oblicz wartość energii potencjalnej piłki na wysokości 4 m nad ziemią.

16.2

Bardzo często upraszczamy obliczenia, pomijając opór powietrza, jednak nie odpowiada to

dokładnie sytuacji rzeczywistej. W poniższych zdaniach podkreśl właściwe słowa zapisane drukiem pochyłym, a w dalszej części zdań wpisz uzasadnienia. Jeśli uwzględnimy opór powietrza, to energia potencjalna spadającej piłki na wysokości 4 m nad ziemią jest (mniejsza niż / większa niż / taka sama jak) ta energia w przypadku, gdy opór powietrza nie występuje, ponieważ ……………………………………………………………………………………………

Jeśli uwzględnimy opór powietrza, to energia kinetyczna spadającej piłki na wysokości 4 m nad ziemią jest (mniejsza niż / większa niż / taka sama jak) ta energia w przypadku, gdy opór powietrza nie występuje, ponieważ ……………………………………………………………………………………………

Jeśli uwzględnimy opór powietrza, to całkowita energia mechaniczna spadającej piłki na wysokości 4 m nad ziemią jest (mniejsza niż / większa niż / taka sama jak) ta energia, gdy

opór powietrza nie występuje, ponieważ …………………………………………………………………………………………

Zadanie 17. (NP15)

Jednostką pracy i ciepła jest dżul. Jednostki tej nie można przedstawić w postaci

Zadanie 18. (NP15)

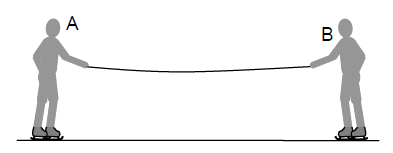
Na lodowisku dwaj chłopcy stojący na łyżwach uchwycili końce liny (rysunek poniżej), po czym zaczęli przyciągać się wzajemnie. Masa każdego z chłopców wynosi 55 kg, a współczynnik tarcia kinetycznego o lód jest równy 0,10.

Oblicz pracę wykonaną w ciągu 3 sekund przeciwko sile tarcia chłopca o lód, jeżeli chłopiec poruszał się z prędkością o wartości 1 m/s.

Zadanie 19. (NP17)

Podczas załadunku na samochód skrzynie z jabłkami są podnoszone na wysokość 1,2 m lub wciągane na tę wysokość po pochyłej desce o długości 4 m. Siła tarcia skrzyni o deskę stanowi 20% ciężaru skrzyni. Osoba podnosząca skrzynię pionowo wykonuje pracę 240 J.

19.1

Oblicz pracę, jaką należy wykonać przeciwko siłom działającym na skrzynię, ciągnąc ją ruchem jednostajnym po desce.

19.2

Wyjaśnij, dlaczego dzięki zastosowaniu deski (równi pochyłej) w opisanym przypadku przemieszczenie skrzyni na daną wysokość staje się łatwiejsze.

Zadanie 20. (NP18)

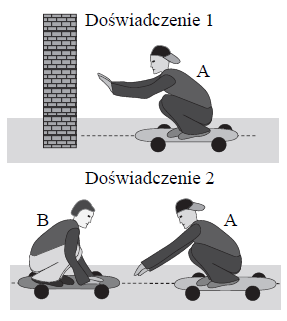
Dwaj chłopcy przeprowadzili doświadczenia. W pierwszym doświadczeniu chłopiec A usiadł na deskorolce stojącej w pobliżu ściany i w pewnej chwili odepchnął się od tej ściany (zobacz rysunek obok). Tuż po odepchnięciu chłopiec uzyskał względem podłoża prędkość w kierunku poziomym, o wartości 4 m/s. Następnie chłopiec A wykonał drugie doświadczenie. Tym razem odepchnął się od drugiej, identycznej deskorolki z nieruchomo siedzącym na niej chłopcem B.

Masy obu chłopców były jednakowe, a deskorolki początkowo spoczywały względem podłoża i ustawione były tak, że mogły poruszać się w przeciwne strony wzdłuż linii prostej (zobacz rysunek obok). Przyjmij, że w każdym z doświadczeń, na skutek odepchnięcia się chłopca A (w pierwszym – od ściany, w drugim – od deskorolki) została wykonana jednakowa praca przez siły wprawiające układy w ruch. Przyjmij także, że w obu doświadczeniach – podczas odepchnięcia, a także tuż po nim – pomijamy skutki działania sił oporów ruchu (z wyjątkiem tarcia statycznego). Załóż ponadto, że masy kółek deskorolki są pomijalnie małe.

20.1

W dwóch poniższych zdaniach podkreśl właściwe określenia, aby zdania były prawdziwe.

1. Po przeanalizowaniu ruchu chłopców siedzących na deskorolkach w drugim doświadczeniu można stwierdzić, że pęd całkowity układu (obu chłopców wraz z deskorolkami) jest po odepchnięciu (taki sam jak / mniejszy niż / większy niż) pęd całkowity układu przed odepchnięciem.

2. Energia kinetyczna, którą uzyskał chłopiec A w drugim doświadczeniu po odepchnięciu się od deskorolki z kolegą, była (taka sama jak / większa niż / mniejsza niż) energia kinetyczna, jaką uzyskał po odepchnięciu się od ściany w pierwszym doświadczeniu.

20.2

Oblicz wartość prędkości, którą uzyskał chłopiec A tuż po odepchnięciu się od drugiej deskorolki.