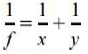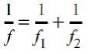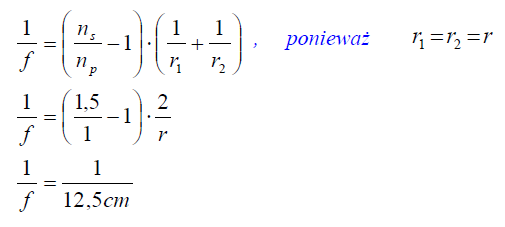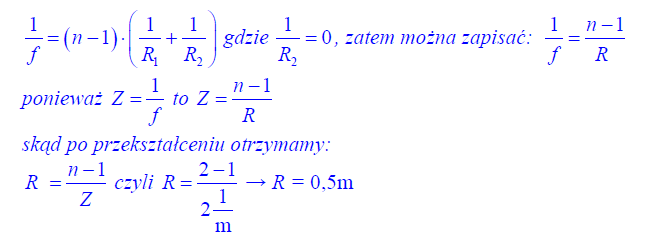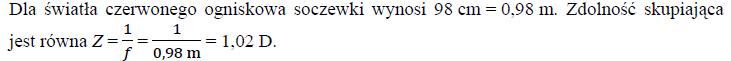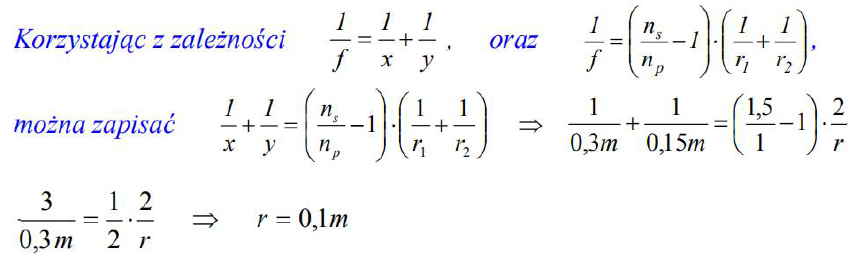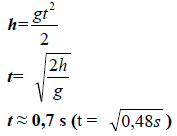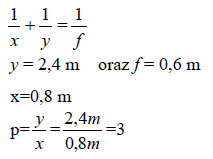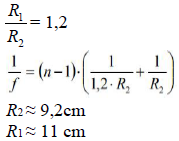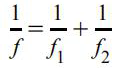Zadania maturalne z Fizyki
Temat: Optyka
Zadania pochodzą z oficjalnych arkuszy maturalnych CKE, które służyły przeprowadzaniu majowych egzaminów. Czteroznakowy kod zapisany przy każdym zadaniu wskazuje na jego pochodzenie: S/N – „stara”/”nowa” formuła; P/R – poziom podstawowy/rozszerzony; np. 08 – rok 2008.
Zbiór zadań maturalnych w formie arkuszy, możesz pobrać >> TUTAJ <<.
Zadanie 1. (SP05)
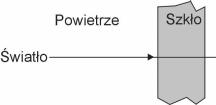
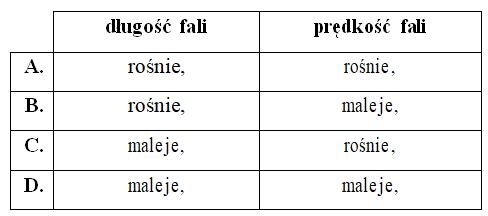
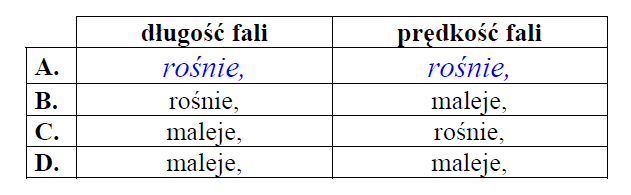
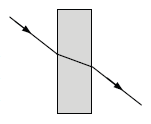
Wiązka światła przechodzi z powietrza do szkła.
Jak podczas tego przejścia zmienią się prędkość, częstotliwość oraz długość fali? Wybierz odpowiedź zawierającą poprawne informacje.
Zadanie 2. (SP05)
Zapisz nazwy trzech urządzeń wykorzystujących w swym działaniu laser.
Czytnik kodów kreskowych, drukarka laserowa, broń laserowa, nagrywarka CD lub DVD, odtwarzacz CD lub DVD, skalpel laserowy, oftalmoskop laserowy, dalmierz laserowy, interferometr laserowy, mikroobrabiarki laserowe, spawarki laserowe, wiertarki laserowe, laser jako źródło światła i inne.
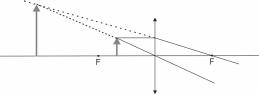
Zadanie 3. (SP05)
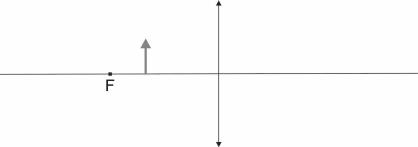
Przed soczewką dwuwypukłą (rys.) umieszczono przedmiot.
Na powyższym rysunku narysuj obraz tego przedmiotu. Zapisz trzy cechy powstałego obrazu.
Zapisanie trzech cech obrazu otrzymanego po przejściu światła przez soczewkę:
Powstanie obraz pozorny, powiększony, prosty.
Zadanie 4. (SP06)
Zdolność skupiająca zwierciadła kulistego wklęsłego o promieniu krzywizny 20 cm ma wartość
- 1/10 dioptrii.
- 1/5 dioptrii.
- 5 dioptrii.
- 10 dioptrii.
Zadanie 5. (SP06)
Podczas odczytu za pomocą wiązki światła laserowego informacji zapisanych na płycie CD wykorzystywane jest zjawisko
- polaryzacji
- odbicia
- załamania.
- interferencji
Zadanie 6. (SP06)
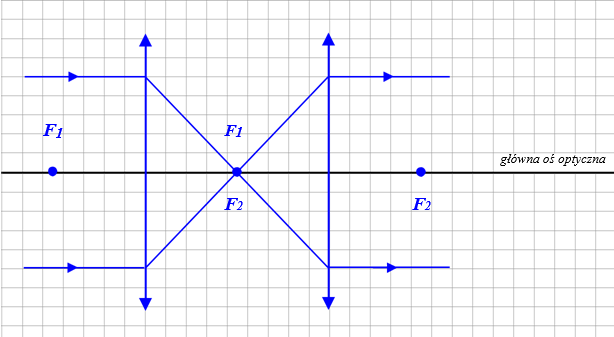
Dwie identyczne soczewki płasko-wypukłe wykonane ze szkła zamocowano na ławie optycznej w odległości 0,5 m od siebie tak, że główne osie optyczne soczewek pokrywają się. Na pierwszą soczewkę wzdłuż głównej osi optycznej skierowano równoległą wiązkę światła, która po przejściu przez obie soczewki była nadal wiązką równoległą biegnącą wzdłuż głównej osi optycznej.
6.1
Wykonaj rysunek przedstawiający bieg wiązki promieni zgodnie z opisaną sytuacją. Zaznacz na rysunku położenie ognisk dla obu soczewek.
6.2
Oblicz ogniskową układu zbudowanego w powietrzu z tych soczewek po złożeniu ich płaskimi powierzchniami. Przyjmij, że promienie krzywizny soczewek wynoszą 12,5 cm, a bezwzględne współczynniki załamania światła w powietrzu oraz szkle wynoszą odpowiednio 1 i 1,5.
6.1
6.2
f=12, 5 cm
Zadanie 7. (SP07)
Monochromatyczna wiązka światła wysłana przez laser pada prostopadle na siatkę dyfrakcyjną. Na ekranie położonym za siatką dyfrakcyjną możemy zaobserwować
- jednobarwne prążki dyfrakcyjne.
- pojedyncze widmo światła białego.
- pojedynczy jednobarwny pas światła.
- widma światła białego ułożone symetrycznie względem prążka zerowego.
Zadanie 8. (SP07)
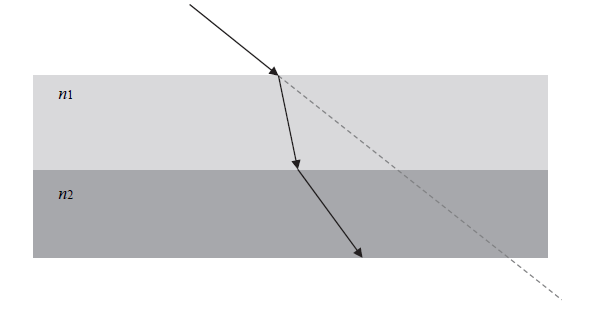
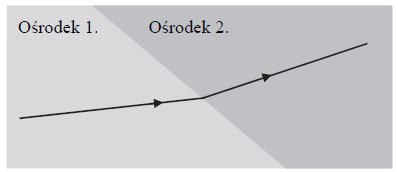
Podczas przejścia wiązki światła z ośrodka o większym współczynniku załamania do ośrodka o mniejszym współczynniku załamania
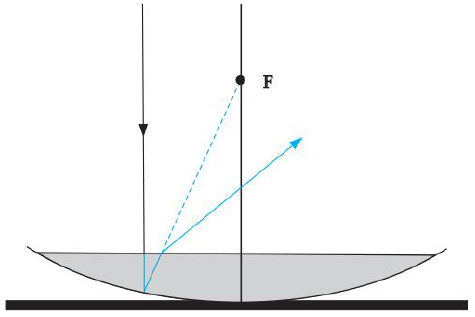
Zadanie 9. (SP07)
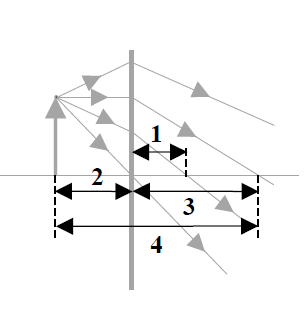
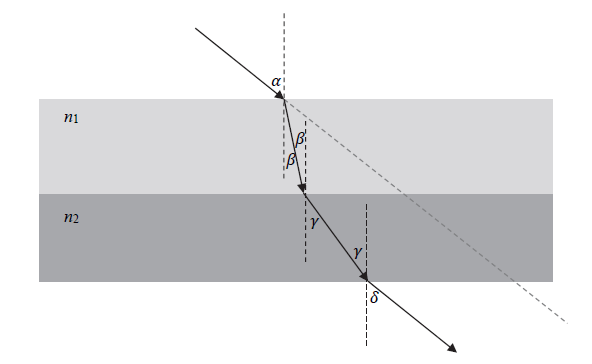
Monochromatyczna wiązka światła biegnąca w powietrzu pada na przeźroczystą płytkę płasko-równoległą tak jak pokazano na rysunku.
9.1.
Oblicz współczynnik załamania materiału, z którego wykonano płytkę. Wykorzystaj informacje zawarte na rysunku oraz tabelę.
9.2.
Zapisz dwa warunki, jakie muszą być spełnione, aby na granicy dwóch ośrodków wystąpiło zjawisko całkowitego wewnętrznego odbicia.
9.1.
9.2.
- Światło musi padać na granicę dwóch ośrodków przy warunku n2 < n1.
- Kąt padania promienia światła α musi spełniać warunek α > αgr.
Zadanie 10. (SP08)
Zdolność skupiająca soczewki płasko-wypukłej wykonanej z materiału o współczynniku załamania równym 2 i umieszczonej w powietrzu wynosi 2 dioptrie.
10.1
Oblicz promień krzywizny wypukłej części soczewki.
10.2
Napisz, czy ta soczewka może korygować wadę dalekowzroczności.
10.1
10.2
Opisana w zadaniu soczewka może korygować wadę dalekowzroczności.
Zadanie 12. (SP09)
Gdy człowiek przenosi wzrok z czytanej książki na odległą gwiazdę, to
| ogniskowa soczewki oka | zdolność skupiająca | |
| A. | rośnie | maleje |
| B. | rośnie | rośnie |
| C. | maleje | maleje |
| D. | maleje | rośnie |
Zadanie 13. (SP09)
Przesyłanie sygnału świetlnego wewnątrz światłowodu jest możliwe dzięki zjawisku
- załamania światła.
- polaryzacji światła.
- rozszczepienia światła.
- całkowitego wewnętrznego odbicia.
Zadanie 14. (SP09)
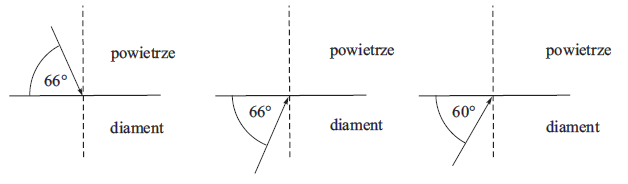
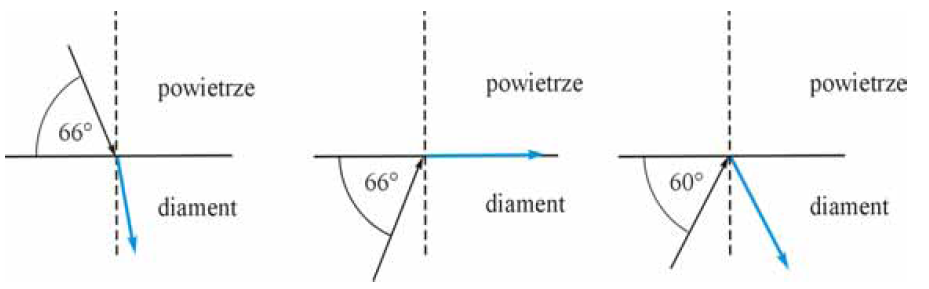
Na granicy dwóch ośrodków o różnych współczynnikach załamania może zachodzić zjawisko całkowitego wewnętrznego odbicia. Naszkicuj, zachowując właściwe relacje kątów, dalszy bieg promieni świetlnych w trzech przedstawionych poniżej sytuacjach. Wykorzystaj informację, że kąt graniczny dla diamentu znajdującego się w powietrzu wynosi 24o.
Zadanie 15. (SP10)
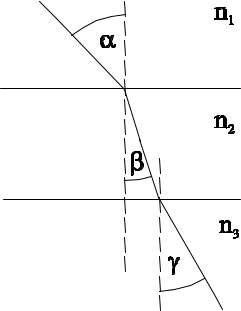
Jednobarwna wiązka światła przechodzi kolejno przez trzy różne ośrodki (rysunek). Jeżeli kąty α, β, γ spełniają warunek: α > γ > β , to bezwzględne współczynniki załamania ośrodków spełniają warunek
- n1 < n2 < n3.
- n1 > n2 > n3.
- n1 < n3 < n2.
- n1 = n2 = n3.
Zadanie 16. (SP10)
Podczas zabiegów kosmetycznych stosuje si ę zwierciadła sferyczne wklęsłe, w celu uzyskania powiększonych obrazów określonych fragmentów twarzy. W odległości 20 cm od takiego zwierciadła, którego ogniskowa wynosi 100 cm, umieszczono świecący przedmiot. Powiększenie otrzymanego obrazu w tym zwierciadle wynosi 1,25.
16.1
Oblicz zdolność skupiającą zwierciadła.
16.2
Oblicz promień krzywizny tego zwierciadła.
16.3
Narysuj konstrukcję ilustrującą powstawanie obrazu w sytuacji opisanej w treści zadania. Zapisz cechy otrzymanego obrazu.
16.1
Z = 1 D
16.2
r = 2 m
16.3
Cechy obrazu:
-pozorny i nieodwrócony (lub prosty)
Zadanie 17. (SP11)
Przed soczewką skupiającą o ogniskowej 20 cm umieszczono świecący przedmiot w odległości 10 cm od soczewki. Otrzymano wówczas obraz
- pozorny, prosty i powiększony.
- pozorny, prosty i pomniejszony.
- rzeczywisty, prosty i powiększony.
- rzeczywisty, odwrócony i powiększony.
Zadanie 18. (SP11)
Wiązkę światła tworzą trzy promienie: czerwony, zielony i niebieski. Po przejściu przez siatkę dyfrakcyjną najbardziej ugięty będzie promień
- niebieski, a najmniej zielony.
- czerwony, a najmniej niebieski.
- zielony, a najmniej czerwony.
- niebieski, a najmniej czerwony.
Zadanie 19. (SP11)
W powietrzu biegnie promień światła jednobarwnego o długości fali λ = 0,60 μm i pada na płytkę szklaną.
19.1
Podaj nazwę wielkości charakteryzującej falę świetlną, która nie zmienia wartości przy przejściu z powietrza do szkła.
19.2
Przyjmując, że prędkość światła w powietrzu wynosi 300 000 km/s, a w szkle 200 000 km/s, oblicz długość fali tego światła po wejściu do szkła.
19.1
- Jest to częstotliwość.
- Jest to okres drgań.
19.2
Ze wzoru v = λf, przy wykorzystaniu jednakowej wartości f, wynika równanie .
Stąd λ2 = 0,4 μm.
Zadanie 20. (SP11)
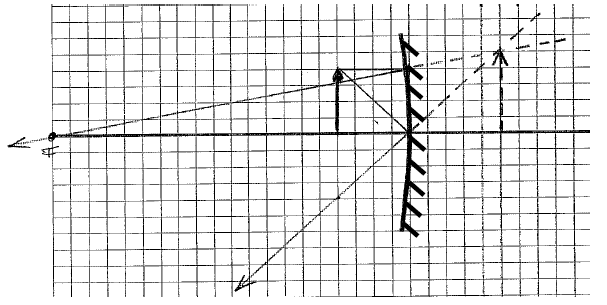
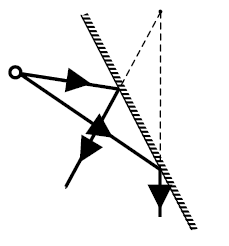
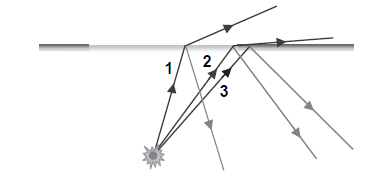
Rysunek przedstawia 2 wybrane promienie wychodzące z jednego punktu świecącej kuli. Starannie narysuj bieg tych promieni po odbiciu od zwierciadła i skonstruuj obraz świecącego punktu.
Zadanie 21. (SP12)
Wiązka światła białego ulega załamaniu w soczewce skupiającej (pojedynczej, tzn. wykonanej z jednego rodzaju szkła). Jeśli ogniskowa soczewki jest równa fc dla światła czerwonego, fn dla światła niebieskiego i fż dla światła żółtego, to
- fc < fn < fż
- fż < fn < fc
- fn < fż < fc
- fc < fż < fn
Zadanie 22. (SP12)
22.1
Opisz doświadczenie pozwalające na wyznaczenie ogniskowej f soczewki skupiają cej, jeśli oprócz tej soczewki masz do dyspozycji małe źródło światła (np. diodę), linijkę i ekran. W opisie wymień niezbędne czynności i wielkości mierzone. Wykonaj rysunek ilustrujący doświadczenie.
22.2
Podaj zależność matematyczną, z której skorzystasz w celu obliczenia wartości ogniskowej. Objaśnij symbole występujące w tej zależności.
22.3
Napisz, w jaki sposób można zwiększyć dokładność pomiaru ogniskowej.
22.1
Na ekranie należy uzyskać ostry obraz źródła, a następnie zmierzyć odległości źródła i ekranu od soczewki.
22.2
Ogniskową f obliczymy ze wzoru : (lub ), gdzie x jest odległością przedmiotu od soczewki, a y – odległością ekranu od soczewki.
22.3
Aby zwiększyć dokładność pomiaru ogniskowej, należy
- wykonać pomiar kilkakrotnie i obliczyć średnią.
- użyć przymiaru o wyższej dokładności.
Zadanie 23. (SP13)
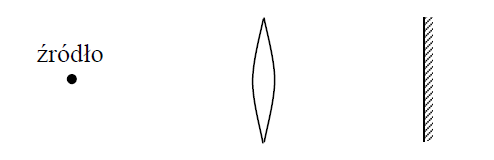
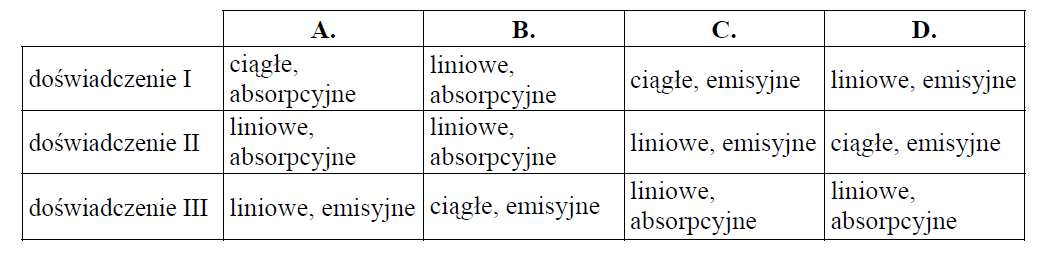
Zbadano widma światła w trzech doświadczeniach:
I – światło wysłane przez żarówkę z włóknem wolframowym wpada bezpośrednio do spektroskopu,
II – światło wysłane przez rozrzedzony gorący gaz wpada bezpośrednio do spektroskopu,
III – światło wysłane przez żarówkę z włóknem wolframowym przechodzi przez naczynie z zimnym gazem i wpada do spektroskopu.
Wybierz kolumnę w tabeli zawierającą poprawne charakterystyki widm.
Zadanie 24. (SP13)
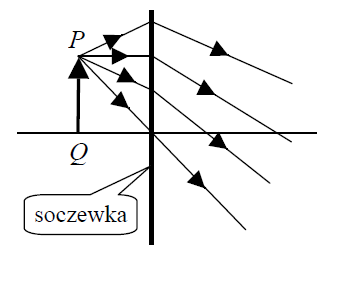
Na rysunku przedstawiono bieg promieni rozchodzących się z punktu P i przechodzących przez soczewkę, o której nie wiemy, czy jest to soczewka skupiająca, czy rozpraszająca.
a) Soczewka przedstawiona na rysunku jest
- skupiająca, a obraz strzałki PQ jest powiększony.
- skupiająca, a obraz strzałki PQ jest pomniejszony.
- rozpraszająca, a obraz strzałki PQ jest powiększony.
- rozpraszająca, a obraz strzałki PQ jest pomniejszony.
b) Odcinek o długości równej ogniskowej soczewki jest obok oznaczony cyfrą
- 1.
- 2.
- 3.
- 4.
a):
A
b):
C
Zadanie 25. (SP13)
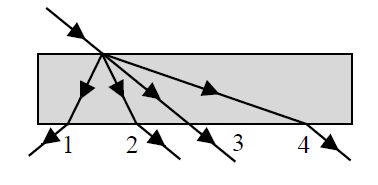
Promień laserowy pada z powietrza na grubą szklaną płytę. Prawidłowy bieg promienia przechodzącego przez płytę jest oznaczony cyfrą
- 1.
- 2.
- 3.
- 4.
Zadanie 26. (SP13)
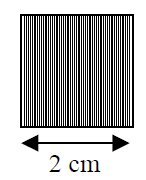
Na płytce szklanej o szerokości 2 cm wyryto stalowym ostrzem 10 000 równoległych i równoodległych bardzo cienkich linii (rys.). Na tę płytkę skierowano prostopadle wiązkę zielonego światła laserowego o długości fali 0,53 μm, a na ekranie ustawionym za płytką zaobserwowano szereg plamek położonych na jednej osi.
26.1
Uzupełnij poniższe zdania, wpisując nazwę przyrządu i nazwę zjawiska fizycznego odpowiedzialnego za wystąpienie plamek.
Opisana płytka nazywana jest ……………………………………………………………… . Plamki powstają wskutek zjawiska ……………………………………………………………… .
26.2
Gdy zamiast światła zielonego użyto światła czerwonego, odległości między plamkami się zwiększyły. Wyjaśnij przyczynę tej zmiany, korzystając z odpowiednich wzorów.
26.3
Oblicz liczbę wszystkich plamek, jakie można obserwować na ekranie przy użyciu światła
o długości fali 0,53 μm, jeżeli zastosuje się opisaną płytkę.
26.1
Uzupełnienie siatką dyfrakcyjną w pierwszej luce, a dyfrakcji i interferencji (lub tylko dyfrakcji, lub ugięcia, lub interferencji) – w drugiej.
26.2
Przyczyną jest większa długość fali światła czerwonego, co na podstawie wzoru nλ = d sin α pociąga za sobą większą odległość między plamkami.
26.3
Do wzoru nλ = d sin α podstawiamy sin α = 1 lub sin α ≤ 1.
Obliczamy
stąd nmax = 3. Zatem liczba plamek jest równa 2nmax + 1 = 7.
Zadanie 27. (SP13)
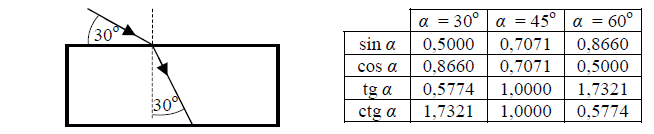
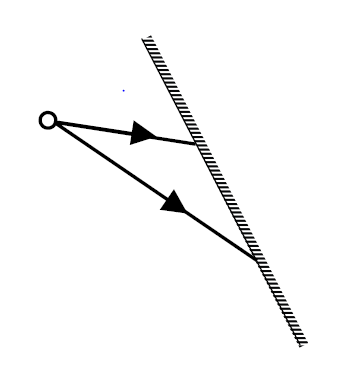
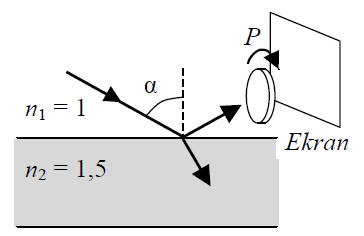
Na płytę szklaną pada promień światła, a światło odbite obserwuje się przez polaryzator P. Przy obrocie polaryzatora wokół osi biegnącej wzdłuż promienia odbitego następuje w pewnych momentach całkowite wygaszenie światła (nie dociera ono do ekranu).
27.1
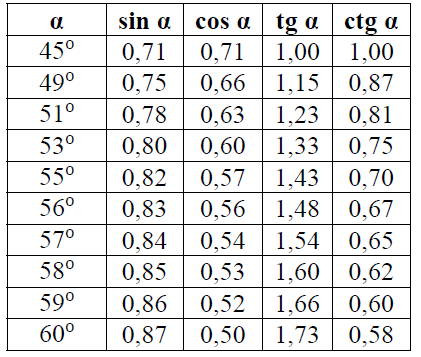
Wykonując niezbędne obliczenia i korzystając z podanej tabeli funkcji trygonometrycznych, napisz przybliżoną wartość kąta padania światła α, dla jakiego zaobserwowano opisane wyżej zjawisko.
27.2
Podkreśl poprawne zakończenie poniższego zdania.
Gdy zmienimy kąt padania promienia i powtórzymy obserwację promienia odbitego przez polaryzator, to podczas obrotu polaryzatora
- nie zaobserwujemy żadnych zmian jasności obrazu.
- zaobserwujemy rozjaśnianie i przygaszanie obrazu, ale bez całkowitego wygaszenia.
- zaobserwujemy rozjaśnianie i całkowite wygaszanie obrazu, ale tylko wtedy, gdy polaryzator będziemy obracać wokół przechylonej osi.
- zaobserwujemy rozjaśnianie i całkowite wygaszanie
27.1
Całkowita polaryzacja występuje dla kąta Brewstera, opisanego wzorem tg α = n. Na podstawie tabeli ustalamy, że α ≈ 56°.
27.2
B
Zadanie 28. (SP14)
Mała kieszonkowa latarka zawiera punktowo świecącą diodę i wklęsłe zwierciadło kuliste o promieniu krzywizny 12 mm. Latarka świeci równoległą wiązką, gdy dioda znajduje się
- w środku krzywizny zwierciadła.
- 12 mm od środka krzywizny w kierunku od zwierciadła.
- 6 mm od środka krzywizny w kierunku zwierciadła.
- 6 mm od środka krzywizny w kierunku od zwierciadła.
Zadanie 29. (SP14)
W obserwacji wnętrza samochodu często przeszkadza nam światło odbite od szyby. Aby zminimalizować ten efekt, obserwator może użyć specjalnych filtrów, które wykorzystują zjawisko
- załamania światła.
- dyfrakcji światła.
- interferencji światła.
- polaryzacji światła.
Zadanie 30. (SP14)
Na powierzchni szkła o współczynniku załamania 1,5 pada wiązka światła o częstotliwości 6,9‧10^14 Hz. Częstotliwość fali tego światła w szkle jest równa:
Zadanie 31. (SP14)
Światło latarki pada na prostopadłościenną płytę szkła i przechodzi na drugą stronę. Po wyjściu z płyty natężenie światła jest mniejsze od natężenia światła padającego. Podaj jedną z przyczyn zmniejszenia natężenia światła.
Przyczyną zmniejszenia natężenia światła może być odbicie światła przy wejściu do płytki i przy wyjściu z niej, a także pochłanianie w szkle.
Zadanie 32. (SP14)
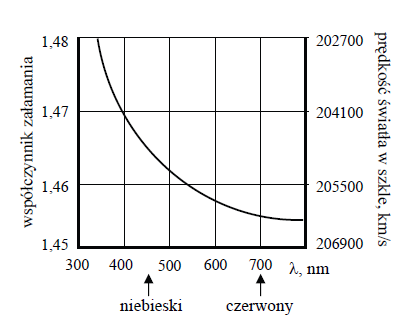
Ogniskowa soczewki zależy od współczynnika załamania materiału (szkła), a współczynnik załamania szkła zależy od długości fali światła. Wykres przedstawia zależność współczynnika załamania pewnego gatunku szkła i odpowiadającej mu prędkości światła w tym szkle od długości fali światła w próżni.
32.1
Wykorzystując dane zawarte na przedstawionym wykresie, wykaż, że ogniskowa dwuwypukłej soczewki wykonanej z danego gatunku szkła ma dla światła czerwonego większą wartość niż dla światła niebieskiego.
32.2
W zakresie światła widzialnego ogniskowa soczewki wynosi od 92 cm do 98 cm. Oblicz zdolność skupiającą opisywanej soczewki dla światła czerwonego.
32.1
Na podstawie wykresu można stwierdzić, że współczynnik załamania dla światła czerwonego jest mniejszy niż dla światła niebieskiego. To znaczy, że soczewka słabiej skupia promienie czerwone, czyli ogniskowa dla światła czerwonego jest większa.
32.2
Zadanie 33. (NP15)
Po przejściu monochromatycznej fali świetlnej z powietrza (np = 1) do szkła o współczynniku załamania ns
A. częstotliwość fali zmaleje ns razy.
B. prędkość fali się nie zmieni.
C. długość fali zmaleje ns razy.
D. okres fali zmaleje ns razy.
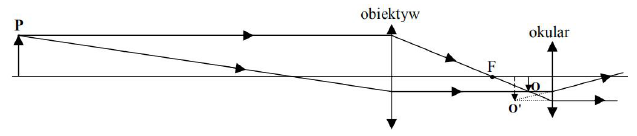
Zadanie 34. (NP15)
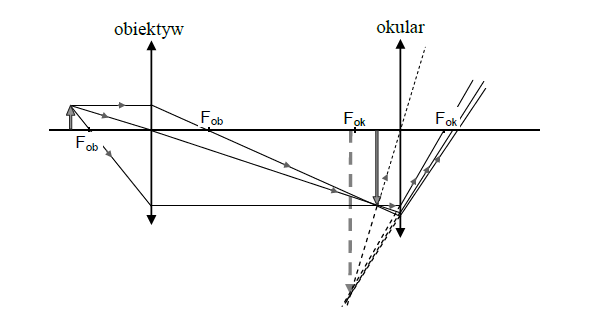
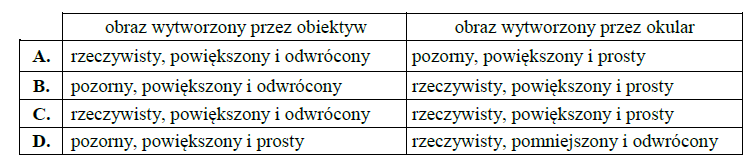
Układ optyczny mikroskopu składa się z obiektywu i okularu. Poniżej przedstawiono schemat ilustrujący powstawanie obrazów w mikroskopie.
W obiektywie i okularze powstają odpowiednio następujące obrazy:
Zadanie 35. (NP15)
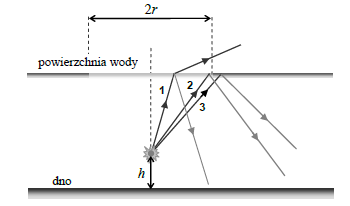
Źródło światła zanurzono w wodzie na wysokości h od dna zbiornika wodnego. Źródło to oświetla powierzchnię wody. Zaobserwowano, że światło docierające ponad powierzchnię wody przechodzi przez tę powierzchnię w obrębie koła o określonym promieniu r.
35.1
Na rysunku przedstawiono bieg trzech promieni padających na powierzchnię wody. Promień 1, dla którego przedstawiono składową załamaną i składową odbitą, pada wewnątrz zaznaczonego koła o promieniu r. Dwa pozostałe promienie 2 i 3 padają w pobliżu granicy obszaru, z którego światło przechodzi ponad powierzchnię wody. Dla tych promieni zaznaczono składowe odbite. Starannie narysuj dalszy bieg składowych załamanych tych promieni (jeśli istnieją).
35.2
Źródło światła przesunięto niżej (bliżej dna zbiornika). Jak zmieni się wartość r promienia
koła, przez które światło przechodzi ponad powierzchnię wody? Zaznacz poprawną odpowiedź wybraną spośród podanych poniżej, a następnie uzasadnij swój wybór. Promień r
A. wzrośnie. B. zmaleje. C. nie zmieni się.
35.1
35.2
A
Zadanie 36. (NP15)
Zdrowe oko dorosłego człowieka ma w przybliżeniu kształt kuli o średnicy 2,5 cm. Odległość dobrego widzenia dla takiego oka wynosi 25 cm. Niektórzy ludzie czytają, trzymając książkę w większej odległości.
36.1
Nazwij wadę wzroku, którą mają ludzie, którzy czytają, trzymając książkę w dużej odległości.
Napisz, czy powinni oni stosować okulary korekcyjne z soczewkami skupiającymi, czy – z rozpraszającymi.
36.2
Oblicz zdolność skupiającą soczewek korekcyjnych dla osób, które bez okularów czytają z odległości 60 cm, a w okularach powinny trzymać książkę w odległości 25 cm. Przyjmij, że odległość oka od soczewki korekcyjnej można pominąć.
36.1
Tą wadą jest dalekowzroczność (lub: nadwzroczność, hyperopia, hypermetropia). Soczewki korekcyjne powinny być skupiające.
36.2
Zadanie 37. (NP16)
Gdy osoba stale nosząca okulary je zdejmuje, często mruży oczy. Może to być skuteczną metodą poprawienia ostrości widzenia, gdyż mrużenie oczu
- powoduje polaryzację światła, co poprawia ostrość widzenia.
- powoduje dyfrakcję światła, co poprawia ostrość widzenia.
- ogranicza obszar soczewki ocznej, przez który przechodzi światło, co zmniejsza rozmycie obrazu powstającego na siatkówce.
- powoduje zwiększenie współczynnika
Zadanie 38. (NP16)
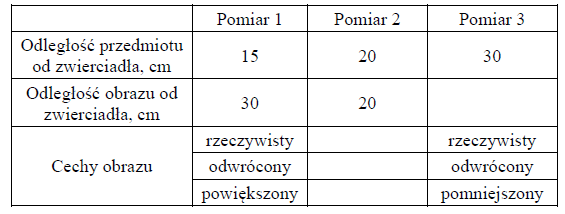
Uczniowie badali obrazy powstające w zwierciadle sferycznym wklęsłym. Wyniki niektórych pomiarów zamieszczono w tabeli.
38.1
Uzupełnij w tabeli cechy obrazu otrzymanego w pomiarze 2.
38.2
Oblicz ogniskową zwierciadła.
38.3
Wpisz do tabeli brakującą odległość obrazu od zwierciadła w pomiarze 3 i uzasadnij tę wartość.
38.1
Uzupełnienie cech obrazu: rzeczywisty, odwrócony, tej samej wielkości.
38.2
Do równania zwierciadła podstawiamy odpowiednie dane (np. x = y = 20 cm) i obliczamy ogniskową zwierciadła f = 10 cm.
38.3
Do tabeli wpisujemy odległość obrazu od zwierciadła w pomiarze 3 równą 15 cm. Uzasadnieniem jest np. porównanie z pomiarem 1 (w równaniu zwierciadła można zamienić x z y) lub obliczenie wartości y z równania zwierciadła z przyjęciem x = 30 cm oraz f = 10 cm.
Zadanie 39. (NP16)
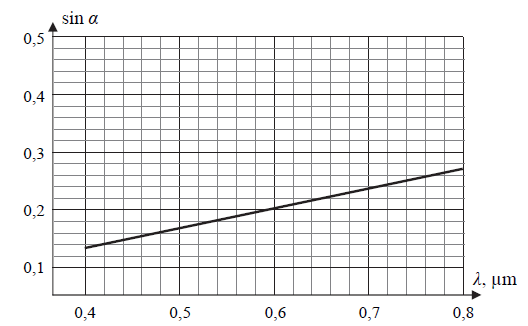
Na siatkę dyfrakcyjną skierowano prostopadle do niej promień światła białego i na ekranie obserwowano powstałe widmo I rzędu. Na poniższym diagramie przedstawiono zależność sinusa kąta ugięcia α od długości fali światła λ. Zwróć uwagę na to, że punkt przecięcia osi nie pokrywa się z zerem.
39.1
Na podstawie diagramu oblicz odległość między rysami siatki.
39.2
Na podanym diagramie dorysuj zależność sin α od λ dla widma II rzędu.
39.1
39.2
Zadanie 40. (NP16)
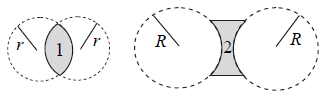
Dwie soczewki 1 i 2 wycięto z tego samego materiału tak, jak pokazano na rysunku. Promienie sfer będących powierzchniami soczewek są większe dla soczewki 2. Oceń poprawność poniższych zdań. Zaznacz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe. Zdania C i D dotyczą bezwzględnych wartości ogniskowych
Zaznaczenie A – F, B – P, C – P i D – F.
Zadanie 41. (NP17)
Na rysunku przedstawiono przedmiot w postaci strzałki i jego obraz utworzony przez soczewkę skupiającą po prawej stronie soczewki. Jeżeli przedmiot przesuniemy do punktu X, to jego obraz powstanie w punkcie oznaczonym małą literą
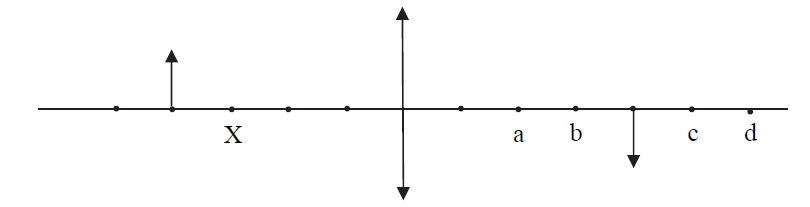
- a.
- b.
- c.
- d.
Zadanie 42. (NP17)
Podczas doświadczalnego wyznaczania ogniskowej soczewki skupiającej uczniowie obserwowali na ekranie rzeczywisty i pomniejszony obraz przedmiotu. Mierzyli dwie odległości:
d – odległość pomiędzy przedmiotem i ekranem (około 90 cm),
y – odległość pomiędzy soczewką i ekranem (około 10 cm).
Do dyspozycji mieli krótką linijkę o długości 12 cm, z podziałką 1 mm oraz długą linijkę o długości 100 cm, z podziałką 0,5 cm.
42.1
Napisz, której linijki powinni użyć uczniowie do pomiaru odległości d, a której – do pomiaru odległości y. Uzasadnij swoje wybory dla każdej z linijek. W uzasadnieniu powołaj się na niepewności pomiarowe mierzonych wielkości.
42.2
Wzór, z którego można obliczyć ogniskową soczewki skupiającej, dysponując wynikami pomiarów odległości d oraz y, ma postać:
Wyprowadź ten wzór.
42.1
Szacowanie niepewności pomiaru odległości d krótką linijką:
Pomiar odległości d równej około 90 cm linijką o długości 12 cm z podziałką 1 mm wymaga wykonania 8 pomiarów, każdy obarczony niepewnością 1 mm. W związku z tym niepewność tego pomiaru wynosi 8 mm.
Szacowanie niepewności pomiaru odległości d długą linijką:
Pomiar odległości d równej około 90 cm linijką o długości 100 cm z podziałką 0,5 cm wymaga wykonania 1 pomiaru, obarczonego niepewnością 0,5 cm. W związku z tym niepewność tego pomiaru wynosi 0,5 cm.
Uzasadnienie wyboru linijki do pomiaru d:
Niepewność w pomiarach krótszą linijką ale z dokładniejszą podziałką jest większa niż niepewność pomiaru długą linijką, ale z większą podziałką: 0,8 cm > 0,5 cm. Dlatego do Strona 13 z 18 pomiaru wybieramy linijkę dłuższą, ponieważ w całym pomiarze chcemy mieć mniejszą niepewność pomiarową.
Uzasadnienie wyboru krótszej linijki do pomiaru y:
Do pomiaru odległości y równej około 10 cm wystarczyłby jeden pomiar krótką lub długą linijką. W związku z tym niepewność w tym jednym pomiarze wynosi tyle, co podziałka na danej linijce i jest mniejsza dla krótkiej linijki: 0,1 cm < 0,5 cm. Dlatego do pomiaru odległości y wybieramy krótszą linijkę (o mniejszej podziałce).
42.2
Zadanie 43. (NP17)
Wiadomo, że promień światła po przejściu przez płytkę równoległościenną, umieszczoną w powietrzu, biegnie dalej wzdłuż prostej równoległej do prostej, wzdłuż której promień pada na płytkę (patrz rysunek). Przyjmij, że bezwzględny współczynnik załamania dla powietrza jest równy 1.
43.1.
Promień światła przechodzi przez dwie równoległościenne warstwy o różnych bezwzględnych współczynnikach załamania. Przechodząc przez te warstwy, ulega załamaniu na każdej z trzech równoległych do siebie powierzchni granicznych. Oznacz na rysunku kąty padania i załamania, a następnie zapisz prawo załamania światła dla wszystkich trzech powierzchni, na których promień światła ulega załamaniu. Napisz, czy proste, wzdłuż których poruszają się promień padający na obie warstwy i promień, który przeszedł przez obie warstwy, są równoległe.
43.2.
Wiadomo, że jedna z warstw na rysunku wykonana jest ze szkła, a druga – z lodu.
Współczynnik załamania szkła jest równy 1,52, a współczynnik załamania lodu wynosi 1,31.
Uzupełnij poniższe zdanie.
Widoczna na rysunku w zadaniu 20.1 warstwa n1 wykonana jest ………………………. , ponieważ
……………………………………………………………………………………………………………………………………
43.1.
43.2.
Widoczna na rysunku w zadaniu 20.1 warstwa n1 wykonana jest ze szkła, ponieważ kąt pomiędzy promieniem a normalną do powierzchni granicznej – zgodnie z prawem załamania – jest mniejszy w tym ośrodku (tutaj n1), w którym współczynnik załamania jest większy (dla szkła).
Zadanie 44. (NP18)
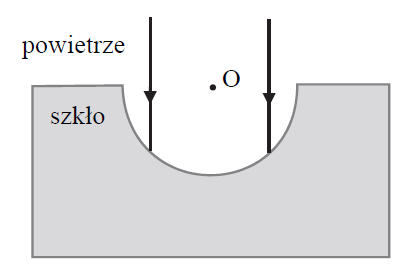
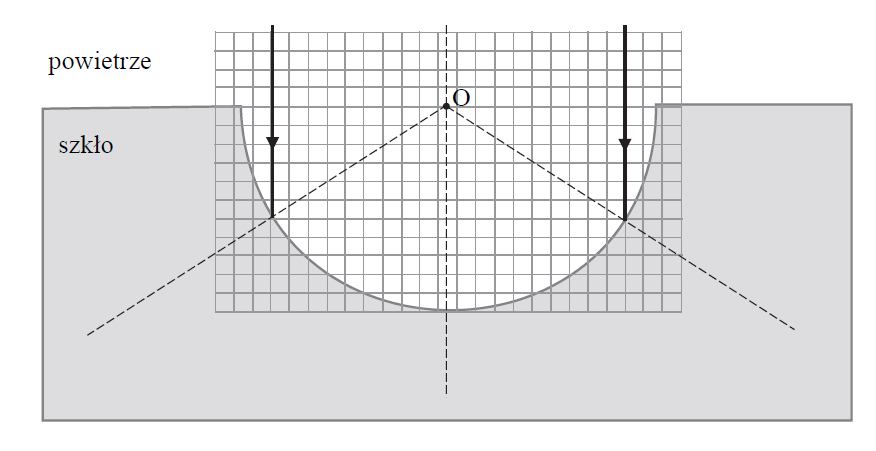
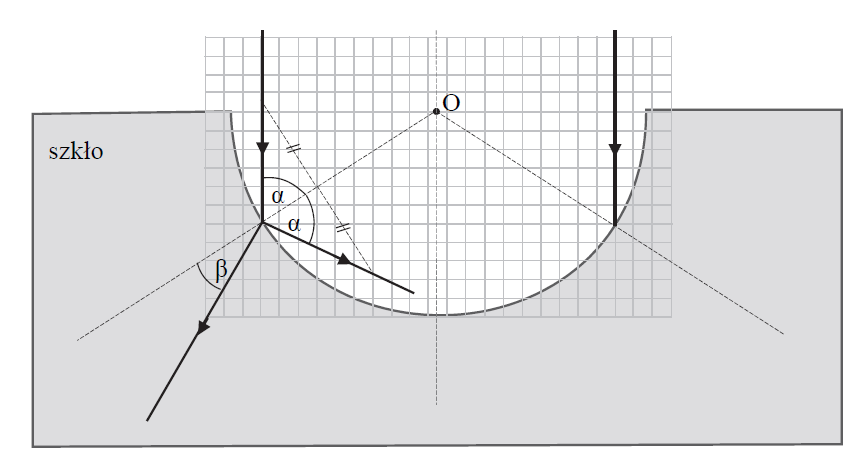
Wiązka światła monochromatycznego pada w kierunku pionowym z powietrza na kuliste zagłębienie wydrążone w szklanym bloku. Rysunek obok przedstawia przekrój szklanego bloku pionową płaszczyzną zawierającą środek wydrążenia (punkt O), a także ukazuje fragmenty dwóch wybranych promieni wiązki światła.
44.1
Na rysunku poniżej dorysuj dalszy bieg jednego z promieni tej wiązki: w powietrzu – po częściowym odbiciu od granicy powietrza i szkła, oraz w szkle – po wniknięciu do szkła. Uwzględnij prawidłowe relacje (większy, mniejszy, równy) pomiędzy odpowiednimi kątami.
Uwaga: odcinki przerywane oraz kratka mogą pomóc w konstrukcji.
44.2
Kuliste zagłębienie w szklanym bloku wypełniono całkowicie pewną cieczą, a wiązkę światła skierowano pionowo w dół – podobnie jak poprzednio. Zaobserwowano, że kierunek promieni po przejściu przez granicę ośrodków cieczy i szkła był taki sam jak kierunek promieni biegnących w powietrzu i cieczy (zobacz rysunek obok). Napisz, jakimi własnościami optycznymi powinna charakteryzować się ta ciecz, aby opisany bieg promieni był możliwy. Uzasadnij swoją odpowiedź.
44.1
44.2
Opisany w zadaniu bieg promieni będzie możliwy, gdy bezwzględny współczynnik załamania dla tej cieczy jest równy bezwzględnemu współczynnikowi załamania szkła, w którym wykonano wydrążenie. W takiej sytuacji, na mocy prawa Snelliusa, kąt załamania promienia w cieczy będzie równy kątowi padania promienia na granicę cieczy i szkła.
Lub Opisany w zadaniu bieg promieni będzie możliwy, gdy prędkość światła w tej cieczy równa jest prędkości światła w szkle, w którym wykonano wydrążenie. W takiej sytuacji, na mocy prawa Snelliusa, kąt załamania promienia w cieczy będzie równy kątowi padania promienia na granicę cieczy i szkła.
Uwaga! Uznawane są odpowiedzi, w których powołano się na równość „gęstości optycznych”
cieczy i szkła.
Zadanie 45. (NP19)
Poniżej przedstawiono przybliżone wartości funkcji trygonometrycznych wybranych kątów.
Światło pada z powietrza na powierzchnię szkła. Kąt padania światła na tę powierzchnię jest równy 58º, a promień odbity od powierzchni szkła jest całkowicie spolaryzowany liniowo. Współczynnik załamania światła dla materiału, z którego wykonane jest szkło, wynosi około
A. n ≈ 1,2 B. n ≈ 0,85 C. n ≈ 1,6 D. n ≈ 0,63
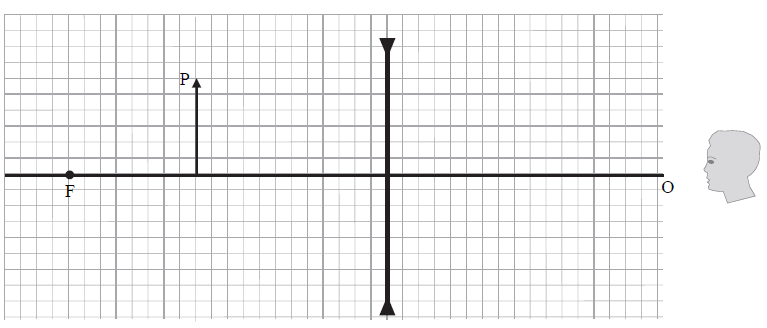
45.1
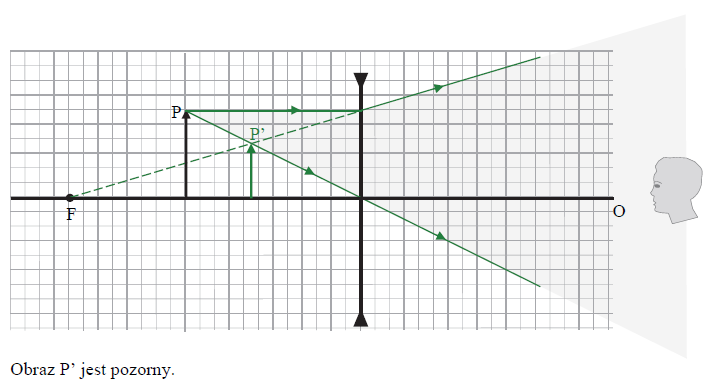
Na rysunku poniżej przedstawiono symbol soczewki rozpraszającej, oś optyczną O soczewki, przedmiot P ustawiony na osi optycznej oraz ognisko F soczewki. Obserwator patrzący z prawej strony soczewki widzi obraz P’ przedmiotu P. Narysuj bieg wybranych promieni charakterystycznych przechodzących przez soczewkę i wychodzących z końca strzałki oznaczającej przedmiot P. Konstrukcyjnie – za pomocą promieni charakterystycznych i ich przedłużeń – wyznacz położenie obrazu P’ przedmiotu P i narysuj ten obraz. Zapisz czy obraz jest rzeczywisty, czy – pozorny.
45.2.
Szklana soczewka dwuwklęsła znajduje się w powietrzu. Ogniskowa tej soczewki jest równa co do wartości bezwzględnej 0,67 m. W odległości 0,4 m od soczewki, na jej osi optycznej, ustawiono przedmiot. Obserwator widzi obraz tego przedmiotu, przy czym obserwator i przedmiot znajdują się po przeciwnych stronach soczewki. Oblicz odległość obrazu przedmiotu P od soczewki.
45.
C
45.1
Obszarem zacieniowanym na szaro oznaczono fragment wiązki promieni wychodzących z soczewki – to jest zbiór tych promieni, które są ograniczone wybranymi promieniami charakterystycznymi.
45.2.
Zadanie 46. (NP19)
Promień światła przechodzi przez granicę ośrodków 1 i 2, tak jak na rysunku poniżej. Niech v1, λ1, f1, n1, oraz v2, λ2, f2, n2, oznaczają: prędkość światła, długość fali światła, częstotliwość światła oraz bezwzględny współczynnik załamania światła odpowiednio dla ośrodków 1 i 2.
Zapisz poprawną relację między wartościami wymienionych wielkości – wstaw
w wykropkowane miejsca w a) – c) jeden ze znaków: >, =, < .
a) f1 ……….. f2
b) v1 ………. v2 λ1 …………. λ2
c) n1 ………. n2
a) f1 = f2
b) v1 > v2 oraz λ1 > λ2
c) n1 < n2
Zadanie 47. (SR06)
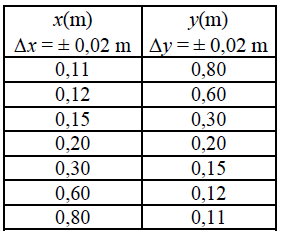
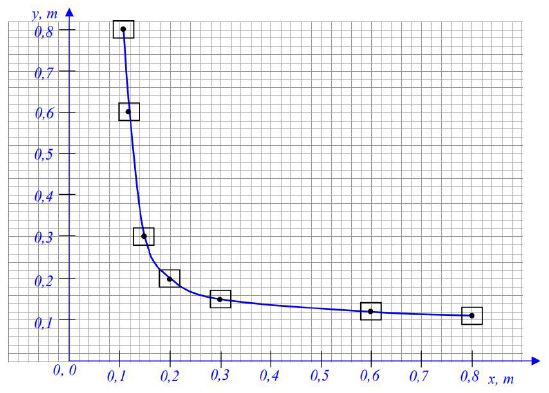
W pracowni szkolnej za pomocą cienkiej szklanej soczewki dwuwypukłej o jednakowych promieniach krzywizny, zamontowanej na ławie optycznej, uzyskiwano obrazy świecącego przedmiotu. Tabela zawiera wyniki pomiarów odległości od soczewki przedmiotu x i ekranu y, na którym uzyskiwano ostre obrazy przedmiotu. Bezwzględne współczynniki załamania powietrza oraz szkła wynoszą odpowiednio 1 i 1,5.
47.1
Oblicz promień krzywizny soczewki wiedząc, że jeśli przedmiot był w odległości 0,3 m od soczewki to obraz rzeczywisty powstał w odległości 0,15 m od soczewki.
47.2
Naszkicuj wykres zależności y(x). Zaznacz niepewności pomiarowe. Wykorzystaj dane zawarte w tabeli.
47.3
Gdy wartość x rośnie, y dąży do pewnej wartości, która jest wielkością charakterystyczną dla soczewki. Podaj nazwę tej wielkości fizycznej oraz oblicz jej wartość.
47.1
47.2
47.3
Zadanie 48. (SR08)
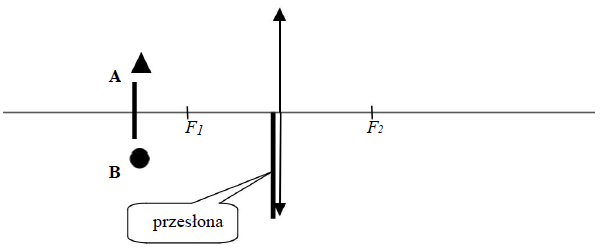
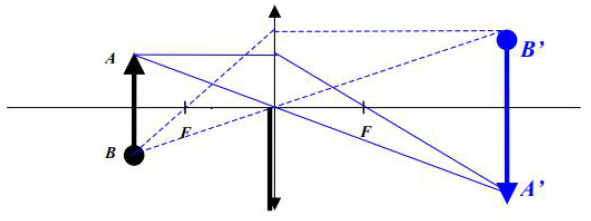
48.1
Na rysunku poniżej przedstawiono świecący przedmiot A-B i soczewkę skupiającą, której dolną część zasłonięto nieprzezroczystą przesłoną. Uzupełnij rysunek, rysując bieg promieni pozwalający na pełną konstrukcję obrazu A’-B’.
48.2
Wykaż, wykonując odpowiednie obliczenia, że przy stałej odległości przedmiotu i ekranu l = x + y, spełniającej warunek l > 4 f, istnieją dwa różne położenia soczewki pozwalające uzyskać ostre obrazy.
Informacja do zadania 48.3 i 48.4
Zdolność skupiającą układu dwóch soczewek umieszczonych obok siebie można dokładnie obliczać ze wzoru
(1) Z = Z1 + Z2 − d⋅Z1⋅Z2 gdzie d – odległość między soczewkami.
Dla dwóch soczewek położonych blisko siebie można zastosować uproszczony wzór
(1) Z=Z1+Z2
48.3
W pewnym doświadczeniu użyto dwóch jednakowych soczewek o zdolnościach skupiających równych 20 dioptrii każda i umieszczonych w odległości 10 cm od siebie.
Wykaż, że jeżeli na układ soczewek, wzdłuż głównej osi optycznej, skierowano równoległą wiązkę światła, to średnica wiązki po przejściu przez układ soczewek nie uległa zmianie.
48.4
Dwie jednakowe soczewki o zdolnościach skupiających 10 dioptrii każda umieszczono w powietrzu w odległości 1 cm od siebie.
Oszacuj bezwzględną ( Z) i względną ( Z/Z) różnicę, jaką uzyskamy, stosując do obliczenia zdolności skupiającej układu soczewek uproszczony wzór (2) zamiast wzoru (1) w opisanej sytuacji.
48.1
48.2
48.3
48.4
Zadanie 49. (SR09)
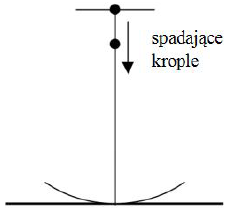
W pokoju na podłodze leży sferyczna, wypolerowana srebrna miska o promieniu krzywizny 1,2 m. Z sufitu znajdującego się na wysokości 2,4 m wzdłuż osi symetrii miski spadają do niej krople wody. Rozwiązując zadanie, pomiń opór powietrza i przyjmij wartość przyspieszenia ziemskiego równą 10 m/s2.
49.1
Zapisz, jakim zwierciadłem (wypukłym/wklęsłym) i (skupiającym/rozpraszającym) jest wewnętrzna powierzchnia miski w tym doświadczeniu.
49.2
Oblicz odległość ogniska tego zwierciadła od sufitu.
49.3
Oblicz czas spadania kropli.
49.4
Określ, jakim ruchem poruszają się względem siebie dwie kolejne spadające krople. Podkreśl właściwą odpowiedź.
| Ruch jednostajny | Ruch jednostajnie
przyspieszony |
Ruch niejednostajnie
przyspieszony |
| Ruch jednostajnie
opóźniony |
Ruch niejednostajnie
opóźniony |
49.5
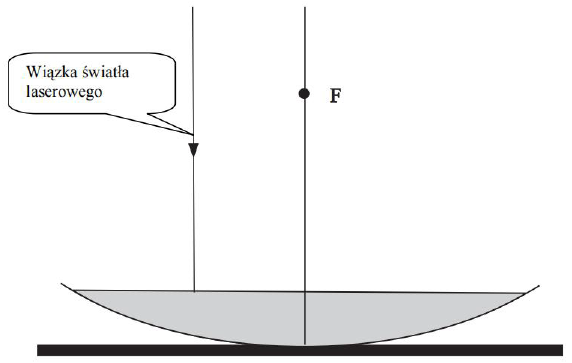
Przy odpowiednim oświetleniu spadającej kropli, w pewnym jej położeniu, na suficie powstaje ostry obraz kropli.
- Wykaż, że obraz kropli na suficie jest wtedy powiększony trzykrotnie, przyjmując, że ogniskowa zwierciadła wynosi 0,6 m.
- Uzupełnij poniższe zdanie, wpisując pozostałe dwie cechy obrazu kropli.
Obraz kropli na suficie jest powiększony, ………………………………… i ………………………………….
49.6
Po pewnym czasie miska wypełniła się wodą.
Przedstaw na rysunku dalszy bieg promienia świetlnego wiązki ś wiatła laserowego skierowanego na powierzchnię wody równolegle do głównej osi optycznej zwierciadła. Wykorzystaj informację, że zaznaczony na rysunku punkt F, jest ogniskiem zwierciadła przed wypełnieniem wodą.
49.1
zwierciadło wklęsłe i skupiające
49.2
f=
=0,6 m
d = 1,8 m
49.3
49.4
ruch jednostajny
49.5
Obraz kropli na suficie jest powiększony, rzeczywisty i odwrócony
49.6
Zadanie 50. (SR10)
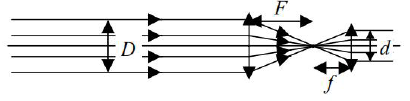
W słoneczny dzień zapalono kawałek suchego drewna, używając szklanej soczewki skupiającej o średnicy 3 cm i ogniskowej 10 cm. Użycie takiej soczewki spowodowało 900–krotny wzrost natężenia oświetlenia drewna.
Średnicę obrazu Słońca otrzymanego za pomocą soczewki obliczamy z równania d = α·f, gdzie α jest wyrażonym w radianach kątem, pod którym widać tarczę Słońca, a f ogniskową soczewki. Natężenie oświetlenia I definiuje się następująco:
50.1
Oblicz zdolność skupiającą tej soczewki.
50.2
Oblicz średnicę obrazu Słońca otrzymanego przy użyciu powyższej soczewki, wiedząc, że tarczę Słońca widać pod kątem 0,01 radiana.
50.3
Oblicz długość promieni krzywizn tej soczewki, jeżeli wykonano ją ze szkła o bezwzględnym współczynniku załamania równym 1,5, a iloraz promieni krzywizn wynosi 1,2.
50.4
Średnica obrazu Słońca uzyskanego przy pomocy soczewki opisanej w zadaniu jest 30 razy mniejsza od średnicy soczewki. Wykaż, że użycie takiej soczewki do zapalenia drewna powoduje 900–krotny wzrost natężenia oświetlenia drewna. Zaniedbaj straty energii pochłanianej w soczewce oraz odbijanej przez jej powierzchnię.
50.5
Według legendy wojska greckie, zgodnie z radą Archimedesa, podpaliły drewniany okręt rzymski, kierując na niego promienie Słońca odbite od płaskich, wypolerowanych, idealnie odbijających światło tarcz obronnych. Zakładając, że każdy żołnierz dysponuje jedną tarczą oraz że promienie świetlne padające ze Słońca i odbite od tarcz są wiązkami równoległymi, oszacuj minimalną liczbę żołnierzy, którzy mogliby tego dokonać. Zapisz warunek, jaki musi być spełniony, aby ich działania mogły spowodować oczekiwany skutek.
50.1
Z = 10 D
50.2
d = α·f
d = 1 mm lub d = 0,1 cm
50.3
50.4
-Energia promieniowania padającego na soczewkę jest taka sama jak energia w otrzymanym obrazie Słońca E1 = E2
-Powierzchnia soczewki oraz powierzchnia obrazu Słońca są proporcjonalne do kwadratu ich średnicy S ~ d
-Stosunku natężenia oświetlenia powierzchni drewna i powierzchni soczewki
I1/I2=900
50.5
n = 900
(lub n = 899 w przypadku, gdy odpowiedź zawiera wyjaśnienie, że żołnierze kierują
odbite promienie słoneczne na oświetloną powierzchnię statku)
zapisanie dodatkowego warunku, np.:
Promienie odbite od tarcz żołnierzy muszą oświetlać/być skierowane w jedno miejsce na statku.
Zadanie 51. (SR11)
Uczniowie zbudowali lunetę Keplera z dwóch szklanych soczewek dwuwypukłych – obiektywu o ogniskowej 50 cm i okularu o ogniskowej 5 cm. Prawe ognisko obiektywu i lewe ognisko okularu się pokrywają (zob. rys.). Uwaga: na rysunku stosunek ogniskowych nie odpowiada danym liczbowym.
51.1
Uzupełnij poniższe zdania. W pierwszym z nich wpisz odpowiednio lewo lub prawo, pomijając ewentualne przesunięcie pionowe.
Gdy przedmiot P oddala się od lunety, obraz O przesuwa się w ………………, a obraz O’ przesuwa się w ………………. . Gdy P jest bardzo daleko (tak, że wiązka padająca na obiektyw może być uznana za równoległą), obraz O znajdzie się ……………………………………, a wiązka wybiegająca z okularu będzie ………………………………. .
51.2
Opisz, czym różni się obraz nieba widziany przez lunetę od obrazu widzianego przez lunetę odwróconą (gdy patrzymy od strony obiektywu).
51.3
Okular jest soczewką symetryczną i wykonaną ze szkła o współczynniku załamania 1,5 względem powietrza. Oblicz promień krzywizny powierzchni tej soczewki.
51.4
Na opisaną lunetę o średnicy obiektywu 7 cm pada wiązka równoległa do osi. Wykonaj odpowiedni rysunek i wykaż, ż e minimalna średnica okularu niezbędna do tego, aby cała wiązka wpadająca do obiektywu trafiła do okularu, wynosi 7 mm.
51.5
Średnica obiektywu lunety wynosi 7 cm, a średnica okularu wynosi 7 mm (patrz zadanie 3.4). Średnica okularu jest równa średnicy źrenicy oka przystosowanego do widzenia w ciemności. Je śli gwiazda leżąca w odległości 40 lat świetlnych jest z trudem dostrzegalna gołym okiem, to w jakiej maksymalnej odległości może le że ć identyczna gwiazda, aby można ją było dostrzec przez tę lunetę? Zapisz odpowiedź i ją uzasadnij. Pomiń pochłanianie światła w przestrzeni kosmicznej.
Wskazówka: O możliwości zobaczenia gwiazdy decyduje moc światła wpadającego do oka obserwatora.
51.6
Oko ludzkie jest najbardziej wrażliwe na światło o długości fali 550 nm, a jego czułość (minimalna energia wywołująca wrażenie świetlne) wynosi 7·10–18 J. Oblicz minimalną liczbę fotonów o długości fali 550 nm, które muszą równocześnie wpaść przez źrenicę oka, aby wywołać wrażenie świetlne.
51.1
Gdy przedmiot P oddala się od lunety, obraz O przesuwa się w lewo, a obraz O’ przesuwa się w lewo. Gdy P jest bardzo daleko (tak, że wiązka padająca na obiektyw może być uznana za równoległą), obraz O znajdzie się w punkcie F, a wiązka wybiegająca z okularu będzie równoległa.
51.2
Przykłady poprawnej odpowiedzi
- Obraz nieba widziany przez lunetę odwróconą jest pomniejszony.
- Zmaleją odległości kątowe między gwiazdami.
- Te obrazy różnią się powiększeniem.
- Te obrazy różnią się jasnością gwiazd.
51.3
Podstawiamy dane do wzoru na ogniskową soczewki symetrycznej
i obliczamy R = 5 cm.
51.4
Z rysunku widać, że
, a ponieważ prawa strona wynosi 10, więc lewa także.
51.5
Jeśli luneta ma 10 -krotnie większą średnicę niż oko, to zbiera 100 razy więcej światła, zatem natężenie światła gwiazdy może być 100 razy słabsze. Światło wybiegające z obiektu punktowego rozkłada się na powierzchni ę kuli. Ta powierzchnia jest 100 razy większa dla kuli o promieniu 10 razy większym, czyli gwiazda może być 10 razy dalej – w odległości 400 lat świetlnych.
51.6
Ze wzoru E = hc/λ znajdujemy energię fotonu Ef = 3,62·10–19 J. Iloraz 7·10–18 J przez energię fotonu wynosi 19,4, zatem odpowiedź brzmi: 20 fotonów (lub 20).
Zadanie 52. (SR15)
W preparacie biologicznym oglądanym przez lupę interesują nas dwa punkty A i B znajdujące się w odległości 0,5 mm od siebie. Obrazy A’ i B’ tych punktów widziane przez lupę znajdują się we wzajemnej odległości 1,25 mm.
52.1.
Korzystając z podanych informacji, zaznacz na poniższym rysunku opisane obrazy A’ i B’. Zachowaj proporcje wielkości i położenia obrazu.
52.2.
Uzupełnij powyższy rysunek tak, aby przedstawić bieg promieni ilustrujący powstawanie opisanego obrazu. Na podstawie tej konstrukcji zaznacz ogniska lupy.
52.3.
Oglądany obraz powstaje w odległości 25 cm od soczewki. Wykaż, że zdolność skupiająca zastosowanej lupy wynosi 6 dioptrii.
52.1.
Przez lupę obserwuje się obraz pozorny (powstający po tej samej stronie soczewki, co przedmiot) i prosty. Zgodnie z danymi powiększenie wynosi 2,5 i jest ono równe stosunkowi odległości |y| między obrazem a soczewką do odległości x między przedmiotem a soczewką. Zatem odległość punktów A’ i B’ od osi optycznej wynosi 5 kratek, a od soczewki 10 kratek, jak na rysunku poniżej.
52.2.
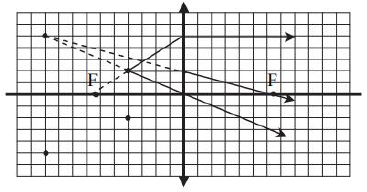
52.3.
Zadanie 53. (NR15)
Ogniskową f układu dwóch cienkich i przylegających do siebie soczewek można obliczyć ze wzoru
gdzie f1 i f2 są ogniskowymi poszczególnych soczewek.
Masz do dyspozycji małe źródło światła (np. świeczkę), ekran, linijkę i dwie soczewki – skupiającą i rozpraszającą. Ogniskowa soczewki skupiającej jest nieznana, ale mniejsza niż bezwzględna wartość ogniskowej soczewki rozpraszającej. Ekran i soczewki są wyposażone w odpowiednie statywy.
Opisz metodę wyznaczenia ogniskowej soczewki rozpraszającej, wykorzystującą podany wzór. Narysuj użyty układ doświadczalny i przedstaw kolejne czynności wybrane spośród podanych niżej. Czynności opisane w punktach e)−h) mogą być powtarzane.
a) Ustawienie świeczki, soczewki skupiającej i ekranu w taki sposób, aby na ekranie powstał ostry obraz świeczki.
b) Ustawienie świeczki, soczewki rozpraszającej i ekranu w taki sposób, aby na ekranie powstał ostry obraz świeczki.
c) Ustawienie świeczki, obu soczewek tuż obok siebie i ekranu w taki sposób, aby na ekranie powstał ostry obraz świeczki.
d) Pomiar średnicy każdej z soczewek.
e) Pomiar wielkości obrazu płomienia na ekranie.
f) Pomiar odległości świeczki od soczewki (lub od zestawu soczewek).
g) Pomiar odległości ekranu od soczewki (lub od zestawu soczewek).
h) Zastosowanie wzoru
i) Przekształcenie wzoru 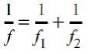
Należy wykonać czynność a) – ustawić świeczkę, soczewkę skupiającą i ekran w taki sposób, aby na ekranie powstał ostry obraz świeczki. Układ doświadczalny jest przedstawiony poniżej.
Należy zmierzyć odległości płomienia świeczki od soczewki i ekranu od soczewki (czynności f) i g)). Po podstawieniu tych odległości do wzoru