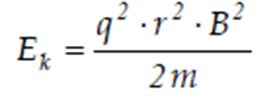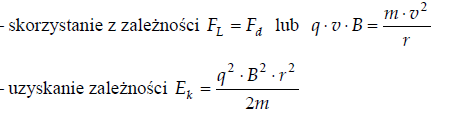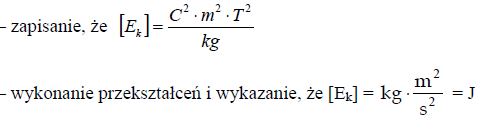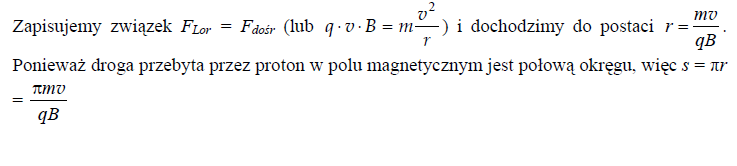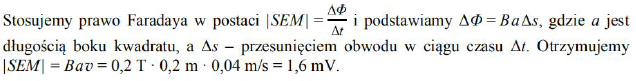Zadania maturalne z Fizyki

Temat: Pole magnetyczne

Zadania pochodzą z oficjalnych arkuszy maturalnych CKE, które służyły przeprowadzaniu majowych egzaminów. Czteroznakowy kod zapisany przy każdym zadaniu wskazuje na jego pochodzenie: S/N – „stara”/”nowa” formuła; P/R – poziom podstawowy/rozszerzony; np. 08 – rok 2008.

Zbiór zadań maturalnych w formie arkuszy, możesz pobrać >> TUTAJ <<.

Zadanie 1. (SP05)

W jednorodnym polu elektrycznym i w jednorodnym polu magnetycznym zostały umieszczone spoczywające ładunki dodatnie. Zapisz poniżej wraz z uzasadnieniem, jak będą zachowywać się ładunki w tych polach. Nie uwzględniaj wpływu siły grawitacji.

Zadanie 2. (SP05)

Wyjaśnij, jakie zjawiska magnetyczne zachodzą podczas podnoszenia za pomocą magnesu żelaznych szpilek rozsypanych na podłodze.

Zadanie 3. (SP06)

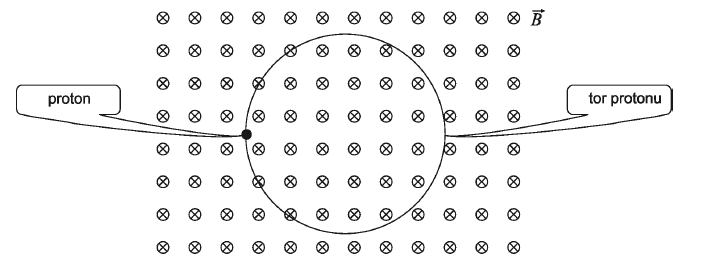
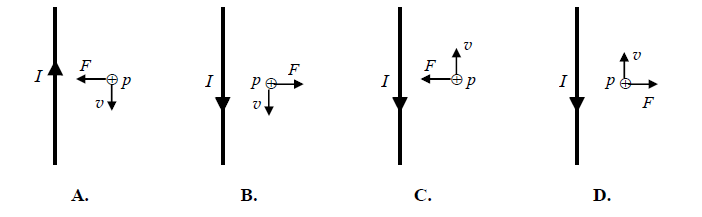
W jednorodnym polu magnetycznym, którego wartość indukcji wynosi 0,1 T, krąży w próżni proton po okręgu o promieniu równym 20 cm. Wektor indukcji pola magnetycznego jest prostopadły do płaszczyzny rysunku i skierowany za tę płaszczyznę.

3.1

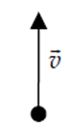
 Zaznacz na rysunku wektor prędkości protonu. Odpowiedź krótko uzasadnij, podając odpowiednią regułę.

 3.2

Wykaż, że proton o trzykrotnie większej wartości prędkości krąży po okręgu o trzykrotnie większym promieniu.

Zadanie 4. (SP07)

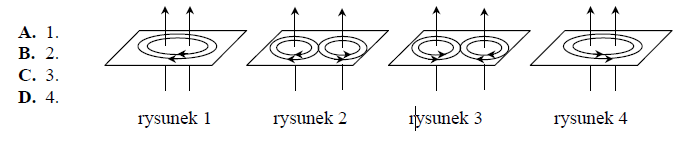
Linie pola magnetycznego wokół dwóch równoległych umieszczonych blisko siebie przewodników, przez które płyną prądy elektryczne o jednakowych natężeniach, tak jak pokazano poniżej, prawidłowo ilustruje rysunek

Zadanie 5. (SP07)

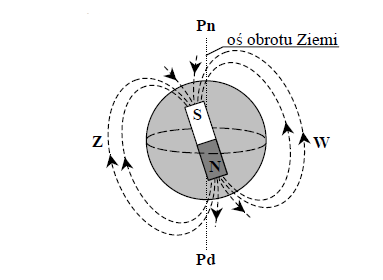
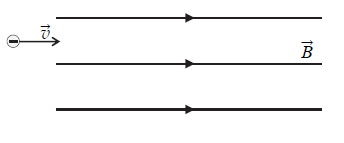
Wiązka dodatnio naładowanych cząstek pochodzenia kosmicznego dociera do Ziemi prostopadle do jej powierzchni w okolicach równika (rys.). W wyniku działania ziemskiego pola magnetycznego zostanie ona odchylona w kierunku

1. północnym.
2. południowym.
3. wschodnim.
4. zachodnim.

Zadanie 6. (SP08)

W cyklotronie do zakrzywiania torów naładowanych cząstek wykorzystuje się

1. stałe pole elektryczne.
2. stałe pole magnetyczne.
3. zmienne pole elektryczne.
4. zmienne pole magnetyczne.

Zadanie 7. (SP09)
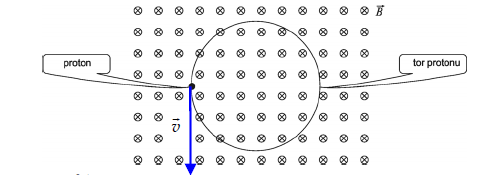
W próżni, w jednorodnym polu magnetycznym o indukcji B, porusza się po okręgu proton o masie m i ładunku q. W pewnej chwili prędkości protonu jest skierowana tak, jak pokazano na rysunku. Wektor indukcji magnetycznej jest skierowany prostopadle do płaszczyzny rysunku ze zwrotem przed płaszczyznę (do patrzącego).

7.1

Zaznacz na rysunku powyżej siłę działającą na proton.

 Informacja do zadań 7.2 i 7.3

Jeśli prędkość protonu jest znacznie mniejsza od prędkości światła, to jego energię kinetyczną, w opisanej powyżej sytuacji, można obliczyć, korzystając ze wzoru:

Gdzie r oznacza promień okręgu po którym porusza się proton.

7.2

Wyprowadź podany powyżej wzór określający energię kinetyczną protonu w polu magnetycznym.

7.3

Wykaż, dokonując rachunku jednostek, że w układzie SI energia kinetyczna protonu opisana wzorem podanym w treści zadania jest wyrażona w dżulach.

Zadanie 8. (SP10)

Wewnątrz zwojnicy o długości 5 cm wytworzono pole magnetyczne o indukcji 2 mT i umieszczono wzdłuż jej osi prostoliniowy przewodnik, przez który płynie prąd o natężeniu 1 mA (rysunek). Wartość siły elektrodynamicznej działającej wewnątrz zwojnicy na przewodnik wynosi

1. 0 N.
2. 10^–9 N.
3. 10^–7 N.
4. 10 N.

Zadanie 9. (SP11)

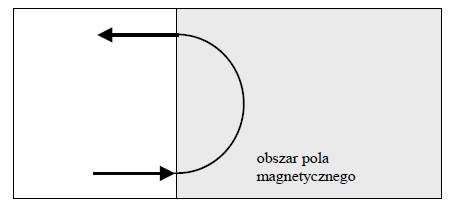
Proton wpada w obszar pola magnetycznego i dalej porusza się w tym polu po półokręgu, po czym wybiega z obszaru pola (rys.).

9.1

9.2

Wyprowadź wzór pozwalający obliczyć drogę s przebytą przez proton w polu magnetycznym w zależności od jego masy m, ładunku e, prędkości v i indukcji pola magnetycznego B.

Zadanie 10. (SP14)

Naładowana cząstka wpada w próżni w obszar jednorodnego pola prostopadle do linii tego pola. Cząstka w obszarze pola porusza się po okręgu. Opisana sytuacja może mieć miejsce w

1. polu magnetycznym.
2. polu grawitacyjnym.
3. polu elektrostatycznym.
4. każdym z trzech pól wyżej wymienionych.

Zadanie 11. (NP15)

Proton porusza się w pustej przestrzeni równolegle do przewodnika, w którym płynie prąd elektryczny. Spośród rysunków przedstawionych poniżej wybierz ten, na którym kierunki i zwroty działającej na proton siły F i prędkości v oraz zwrot przepływu prądu są zgodne z prawami fizyki.

Zadanie 12. (NP15)

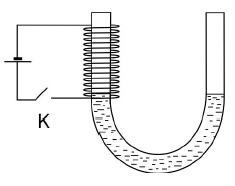
W pewnym doświadczeniu badano właściwości magnetyczne dwóch cieczy o nieznanych właściwościach. Do naczynia w kształcie litery U nalano ciecz 1, a na jedno z ramion tego naczynia nasunięto zwojnicę (patrz rysunek) i zamknięto klucz K. Następnie doświadczenie powtórzono z cieczą 2. Okazało się, że w przypadku cieczy 1 poziom cieczy w ramieniu ze zwojnicą nieznacznie się obniżył, a w przypadku cieczy 2 poziom cieczy w ramieniu ze zwojnicą znacznie się podniósł.

12.1.

Podkreśl poprawne uzupełnienia zdań.

Ciecz 1 wykazuje własności (paramagnetyczne / diamagnetyczne / ferromagnetyczne).

Ciecz 2 wykazuje własności (paramagnetyczne / diamagnetyczne / ferromagnetyczne).

12.2

Podaj przykład substancji ferromagnetycznej. Napisz nazwy dwóch urządzeń, w których są stosowane materiały ferromagnetyczne.

Zadanie 13. (NP16)
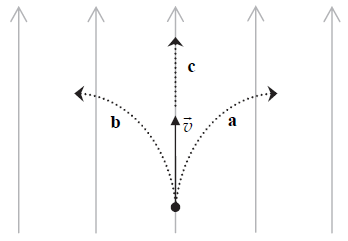
W jednorodne pole magnetyczne, którego linie zaznaczono na rysunku szarym kolorem, wpada proton z prędkością początkową v. Torem ruchu protonu jest w tym przypadku:

1.  fragment łuku okręgu – tor a.
2. fragment łuku okręgu – tor b.
3. fragment prostej – tor c.
4. fragment łuku okręgu w płaszczyźnie prostopadłej do płaszczyzny rysunku

Zadanie 14. (NP17)

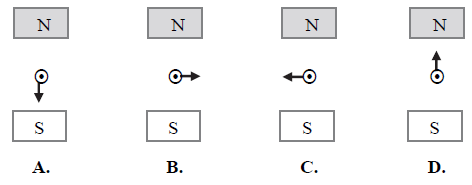
Jeżeli w przewodniku prostoliniowym ustawionym prostopadle do płaszczyzny rysunku płynie prąd w stronę przed płaszczyznę rysunku (w stronę patrzącego), to na ten przewodnik działa siła elektrodynamiczna o takim zwrocie i kierunku, jak na rysunku

Zadanie 15. (NP17)

Zadanie 16. (NP18)

Elektron wpada w obszar jednorodnego pola magnetycznego z prędkością, której kierunek jest równoległy do linii tego pola. Ewentualny wpływ innych pól na ruch elektronu pomijamy. W takiej sytuacji, ten elektron będzie poruszał się dalej w obszarze pola magnetycznego po torze, który jest fragmentem

1. okręgu.
2. paraboli z ramionami skierowanymi ku górze.
3. paraboli z ramionami skierowanymi do dołu.
4. prostej równoległej do linii pola magnetycznego.

Zadanie 17. (NP18)

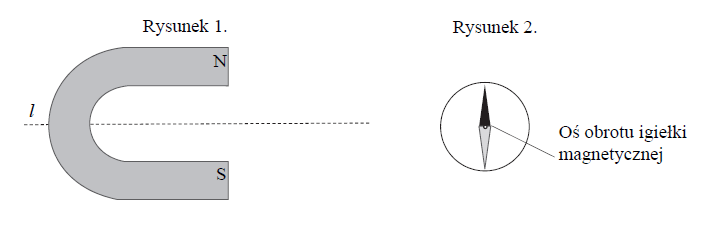
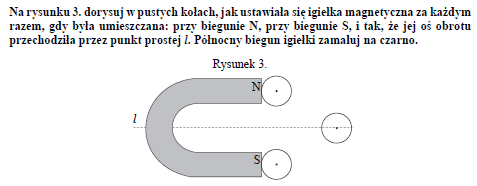
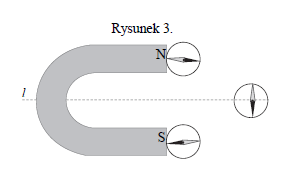
W pobliżu magnesu podkowiastego umieszczano igiełkę magnetyczną. Rysunki 1. oraz 2. przedstawiają oddzielnie magnes oraz igiełkę. Igiełka może obracać się dookoła osi prostopadłej do płaszczyzny rysunku. Bieguny magnesu oznaczono literami N i S. Północny biegun igiełki oznaczono kolorem czarnym, a południowy – szarym. Załóż, że pole magnetyczne pochodzi tylko od magnesu, a kształt linii pola magnetycznego w płaszczyźnie rysunku jest symetryczny względem prostej l.

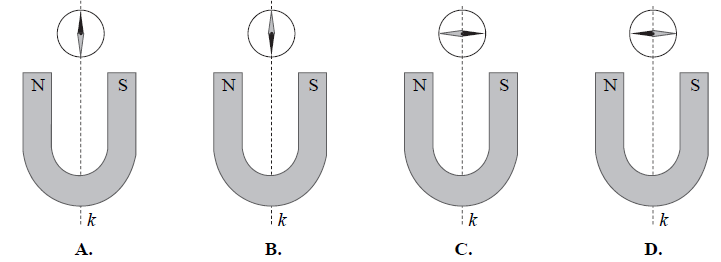
Zadanie 18. (NP19)

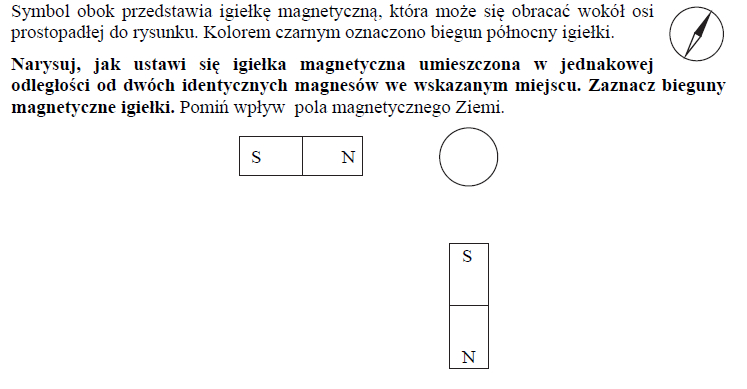
W pobliżu magnesu podkowiastego, w punkcie na linii k, umieszczono igiełkę magnetyczną. Igiełka może obracać się dookoła osi prostopadłej do płaszczyzny rysunku. Kształt linii pola magnetycznego w płaszczyźnie rysunku jest symetryczny względem prostej k. Bieguny magnesu oznaczono literami N i S. Północny biegun igiełki oznaczono kolorem czarnym, a południowy – szarym. Przyjmij, że pole magnetyczne pochodzi tylko od magnesu. Wskaż rysunek przedstawiający prawidłowe ustawienie igiełki w polu magnetycznym magnesu.

Zadanie 19. (SR11)

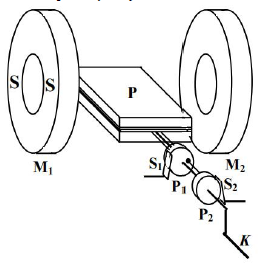
Uczniowie nawinęli izolowany drut miedziany na pudełko od zapałek P, które osadzili na obracającej się osi z dwoma przewodzącymi pierścieniami P1 i P2. Do tych pierścieni podłączyli końce nawiniętego drutu. Do pierścieni były dociśnięte blaszki S1 i S2, od których odprowadzono przewody. Pudełko znajdowało się między dwoma magnesami M1 i M2 o kształcie pierścieni. Wirnik z pudełka od zapałek można było obracać za pomocą korby K. Uczniowie obracali wirnik jednostajnie.

19.1  

Uzupełnij poniższe zdania, wpisując w wolne miejsca wyrażenia dotyczące zasady działania i przemian energetycznych zachodzących w opisanej wyżej prądnicy.

Prądnica skonstruowana przez uczniów do wytwarzania napięcia wykorzystuje zjawisko …………………………………………………………………………………..

Prądnica jest urządzeniem, które zamienia energię …………………………………………… na energię …………………………………………….

19.2  

Lewy magnes M1 ma na swojej lewej powierzchni biegun S, a na prawej (niewidocznej) biegun N. Który biegun powinien być na lewej powierzchni magnesu M2, aby prądnica działała najlepiej?

19.3

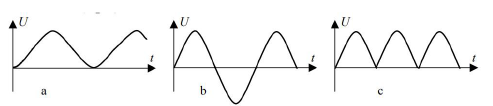
Na którym wykresie – a, b czy c – prawidłowo przedstawiono przebieg czasowy napięcia na wyjściu prądnicy (tzn. między blaszkami S1 i S2)? Zaznacz właściwy podpis.

19.4

Czy w takim położeniu pudełka, jakie zostało przedstawione na rysunku w informacji do zadania, napięcie ma wartość maksymalną, czy równą zero, czy równą wartości skutecznej? Zapisz i uzasadnij odpowiedź.

19.5

Pudełko P ma długość 5 cm i szerokość 2,5 cm, a liczba nawiniętych zwojów jest równa 100. Pole magnetyczne w obszarze zajmowanym przez wirnik można uznać za jednorodne, a jego indukcja ma wartość 0,3 T. Wirnik prądnicy wykonuje 5 obrotów na sekundę. Oblicz maksymalną i skuteczną wartość napięcia na zaciskach prądnicy.

19.6  

Do działającej prądnicy uczniowie dołączyli opornik, a następnie zastąpili go zwojnicą, której opór (zmierzony w obwodzie prądu stałego) był równy oporowi opornika. W obu sytuacjach uczniowie zmierzyli wartość skuteczną natężenia prądu płynącego przez dołączony element. Wyjaśnij, dlaczego te wartości nie były takie same. W którym przypadku natężenie prądu było większe?

19.7  

Czy po wsunięciu żelaznego rdzenia do zwojnicy (zob. poprzedni punkt) wartość skuteczna natężenia prądu wzrosła, zmalała, czy pozostała bez zmiany? Zapisz i uzasadnij odpowiedź.

Zadanie 20. (SR15)

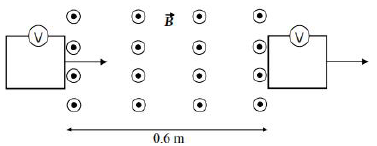
Obwód elektryczny w kształcie kwadratu o boku 20 cm przechodzi ruchem jednostajnym z prędkością o wartości 0,04 m/s przez pole magnetyczne (zob. rysunek). Pole to jest jednorodne w obszarze o szerokości 0,6 m, skierowane prostopadle do płaszczyzny rysunku ze zwrotem przed tę płaszczyznę, a indukcja tego pola ma wartość 0,2 T. Poza wskazanym obszarem pola nie ma (B = 0). W chwili początkowej obwód znajduje się poza obszarem pola i zaczyna w nie wchodzić. W obwodzie znajduje się woltomierz, który w pewnych przedziałach czasu rejestruje wystąpienie napięcia elektrycznego.

Powyższy rysunek jest uproszczony – nie zaznaczono na nim zwojnicy wytwarzającej opisane pole magnetyczne.

20.1.

Na poniższym rysunku a) zaznaczono elektron e znajdujący się wewnątrz przewodnika, z którego wykonano obwód. Narysuj wektor siły elektrodynamicznej (siły Lorentza) działającej na wskazany elektron podczas wchodzenia tego obwodu w pole magnetyczne. W obwodzie bez woltomierza może popłynąć prąd. Na rysunku b) zaznacz zwrot prądu płynącego w obwodzie podczas wychodzenia tego obwodu z pola magnetycznego.

Uzasadnij wybrany kierunek siły na rysunku a) i wybrany zwrot prądu na rysunku b).

20.2.

Wykaż, że napięcie wskazane przez woltomierz podczas wchodzenia obwodu w obszar działania pola wynosi 1,6 mV.

20.3.  

Wykaż, że czas przechodzenia obwodu przez obszar pola magnetycznego wynosi 20 sekund, z czego przez 10 s cały obwód przebywał w obszarze pola.

20.4.  

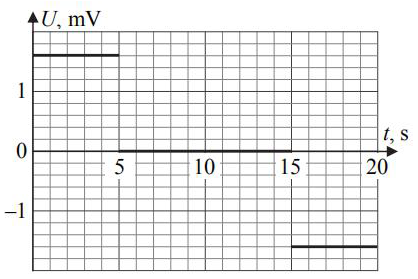
Narysuj wykres zależności napięcia wskazywanego przez woltomierz od czasu. Wykorzystaj niezbędne wartości podane w zadaniach 5.2 i 5.3.

Zadanie 21. (NR15)

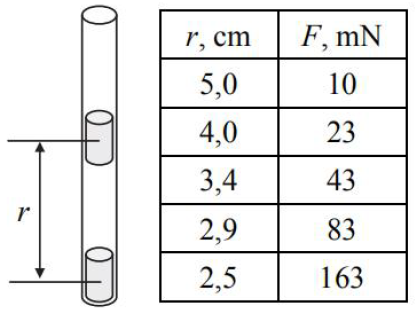
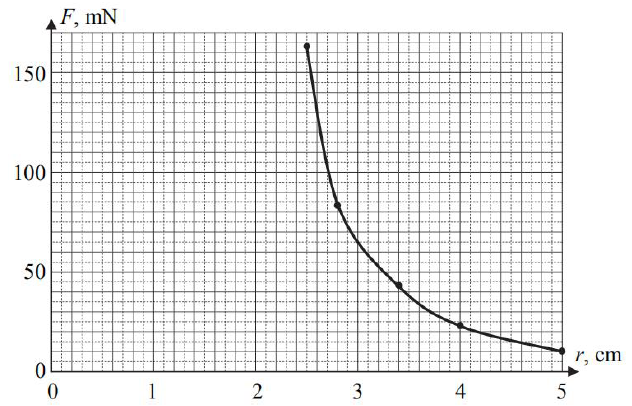
Mamy do dyspozycji silne magnesy w kształcie walca. Umieszczono dwa takie odpychające się magnesy w plastikowej, przezroczystej, pionowo ustawionej rurce i zbadano, jak siła F ich wzajemnego oddziaływania zależy od odległości r pomiędzy ich środkami (rysunek obok). Dolny magnes był unieruchomiony.

Siłę F wyrażono w miliniutonach. Wyniki pomiarów zapisano w tabeli.

Zadanie 21.1.

a) Narysuj wykres zależności F(r).

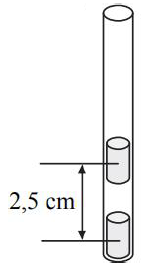
b) Górny magnes zbliżono do dolnego na odległość 2,5 cm (mierzoną między ich środkami – rysunek obok).

Oszacuj, korzystając z wykresu, pracę wykonaną przeciw sile F przy zbliżaniu magnesów, jeśli początkowo ich środki były odległe o 5 cm.

Informacja do zadań 21.2.–21.3.

W następnym doświadczeniu wykonano serię pomiarów czasu spadania jednego magnesu z wysokości 40 cm w pionowo ustawionych rurkach wykonanych z różnych materiałów (rysunek obok).

21.2.

Czas spadku magnesu w plastikowej rurce był równy 0,30 ± 0,03 s.

Sprawdź, wykonując obliczenia, czy w granicach niepewności pomiaru można uznać spadek magnesu za swobodny. Napisz otrzymany wniosek (można lub nie można).

21.3.

Zaznacz właściwe uzupełnienie poniższego zdania wybrane spośród A–C oraz uzasadnienie wybrane spośród 1–3.

Gdy rurkę z plastiku zamieniono na rurkę tej samej średnicy, ale wykonaną z miedzi, czas spadania wyniósł 5,50 s, a ruch magnesu był jednostajny praktycznie na całej długości rurki.

Przyczyną takiego zachowania się magnesu było