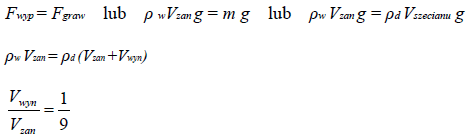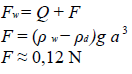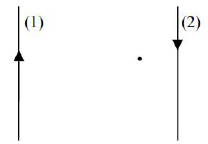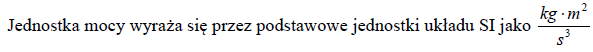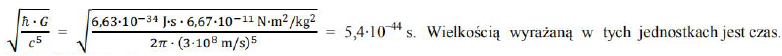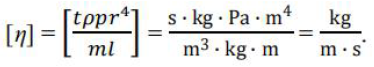Zadania maturalne z Fizyki

Temat: Siły proste

Zadania pochodzą z oficjalnych arkuszy maturalnych CKE, które służyły przeprowadzaniu majowych egzaminów. Czteroznakowy kod zapisany przy każdym zadaniu wskazuje na jego pochodzenie: S/N – „stara”/”nowa” formuła; P/R – poziom podstawowy/rozszerzony; np. 08 – rok 2008.

Zbiór zadań maturalnych w formie arkuszy, możesz pobrać >> TUTAJ <<.

Zadanie 1. (SP05)

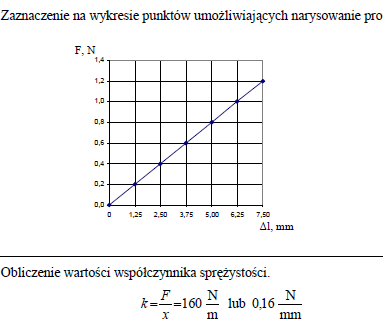
Nić z włókna szklanego poddano mechanicznemu rozciąganiu. W tabelce zamieszczono zależność zmiany długości włókna od przyłożonej siły.

Narysuj wykres zależności siły rozciągającej od wydłużenia nici i oblicz współczynnik sprężystości włókna.

Zadanie 2. (SP10)

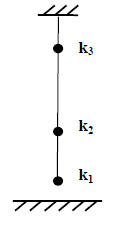
Do pionowo zawieszonej nitki przymocowano 3 niewielkie ołowiane kulki. Odległość między stołem a pierwszą kulką wynosiła 10 cm a odległości pomiędzy kolejnymi kulkami wynosiły 30 cm i 50 cm odpowiednio (rysunek). Następnie przecięto sznurek ponad kulką k3 i kulki zaczęły swobodnie spadać. Czas, po którym pierwsza kulka uderzyła w stół w porównaniu z czasem, jaki upłynął między  derzeniami kolejnych kulek o powierzchnię stołu jest

1. krótszy niż czas między upadkiem kulek k2 i k3.
2. najkrótszym z czasów między upadkiem kolejnych kulek.
3. najdłuższym z czasów między upadkiem kolejnych kulek.
4. taki sam jak czasy między upadkiem kulek k1 i k2 oraz k2 i k3.

Zadanie 3. (SP10)

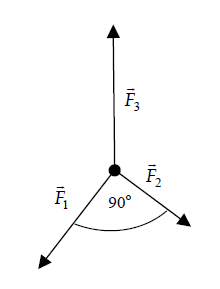
Na rysunku obok przedstawiono układ trzech sił działających na klocek, który pozostawał w spoczynku. Wartości sił wynosiły odpowiednio F1 = 30 N, F2 = 40 N. Oblicz wartość siły F₃.

Zadanie 4. (SP14)

Rozważamy zależność siły tarcia od następujących czynników: siły wzajemnego nacisku ciał, rodzaju stykających się ze sobą powierzchni, stopnia wygładzenia powierzchni oraz wielkości powierzchni styku. Jeśli zmieniamy tylko jeden z tych czterech czynników, to okazuje się, że wartość siły tarcia nie zależy od

1. siły nacisku ciał.
2. rodzaju stykających się powierzchni.
3. wielkości powierzchni styku.
4. stopnia wygładzenia powierzchni.

Zadanie 5. (NP15)

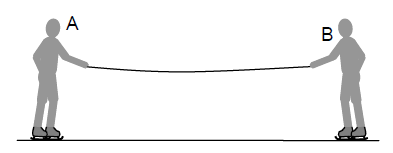
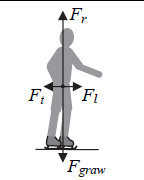
Na lodowisku dwaj chłopcy stojący na łyżwach uchwycili końce liny (rysunek poniżej), po czym zaczęli przyciągać się wzajemnie. Masa każdego z chłopców wynosi 55 kg, a współczynnik tarcia kinetycznego o lód jest równy 0,10.

Narysuj i nazwij wszystkie siły działające na chłopca A podczas jego ruchu jednostajnego.

Proporcje długości strzałek powinny być zgodne z rzeczywistością.

Zadanie 6. (NP19)

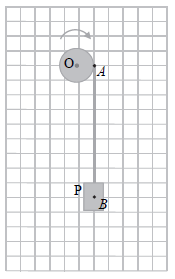
Ciężarek P zawieszono na lekkiej nierozciągliwej nitce nawiniętej na walec. Pod wpływem ciężaru opuszcza się on w dół i jednocześnie wprawia walec w ruch obrotowy względem nieruchomej osi O. Podczas ruchu ciężarka w dół nitka pozostaje napięta, a nawinięta na walec część nitki nie ślizga się po walcu. Masę nitki i opory ruchu pomijamy.

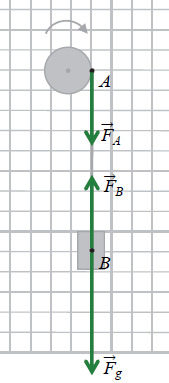
Gdy ciężarek opuszcza się ruchem przyspieszonym to działają na niego dwie siły: F_B – siła reakcji napiętej nitki oraz F_g – siła grawitacji (przyjmij, że obie te siły są zaczepione w punkcie B). Natomiast na walec w punkcie A działa siła F_A – siła reakcji napiętej nitki.

Na rysunku powyżej dorysuj wektory wymienionych sił wraz z ich oznaczeniem. Zachowaj relacje (większy, równy, mniejszy) między wartościami narysowanych wektorów i zapisz te relacje – wstaw w miejsca poniżej jeden ze znaków: >, =, <.

1) FB ………….. Fg 2) FB …………… FA

Zadanie 7. (SR10)

Drewniany sześcian o gęstości 900kg/m i boku a = 5 cm umieszczono w naczyniu z wodą o gęstości 1000kg/m.

7.1  

Oblicz stosunek objętości części wynurzonej (Vwyn) do objętości części zanurzonej (Vzan) sześcianu pływającego w wodzie.

7.2

Oblicz najmniejszą wartość siły, której należałoby użyć, aby cały sześcian znalazł się pod powierzchnią wody.

7.3

Sześcian, opisany w treści zadania, włożono do naczynia zawierającego wodę słoną. Napisz, czy zanurzenie sześcianu w słonej wodzie zmieni się w porównaniu z jego zanurzeniem w wodzie słodkiej. Odpowiedź krótko uzasadnij.

7.4

Do naczynia z wodą i pływającym w niej klockiem dolano oleju o gęstości 850kg/m, w taki sposób, że górna krawędź klocka zrównała się z powierzchnią oleju. Stwierdzono wtedy, że w wodzie znalazła się część klocka o wysokości równej a. Oblicz wartość siły wyporu, z jaką olej działa na zanurzony w nim klocek.

Zadanie 8.

Międzynarodowy Układ Jednostek Miar SI składa się z jednostek podstawowych i jednostek pochodnych. Do jednostek podstawowych należą m.in. metr, sekunda, amper, kelwin, kandela, mol.

8.1

Napisz nazwę jednostki podstawowej niewymienionej powyżej. Napisz nazwę wielkości fizycznej wyrażającej się w tych jednostkach.

8.2

Wyraź jednostkę mocy w jednostkach podstawowych układu SI.

8.3

8.4

Przepływ cieczy przez cienkie rurki zależy między innymi od współczynnika lepkości, oznaczanego symbolem η. Wzór wyrażający masę cieczy m przepływającej w czasie t przez rurkę o długości l i promieniu r ma postać 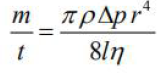 gdzie Δp jest różnicą ciśnień między końcami rurki, a ρ – gęstością cieczy. Wyraź jednostkę

lepkości przez jednostki podstawowe układu SI.

8.5

Każda jednostka układu SI ma swój wzorzec. Definicja ampera jest następująca:

Jeden amper jest to natężenie prądu, który płynąc w dwóch równoległych, prostoliniowych, nieskończenie długich przewodach o znikomo małym przekroju kołowym, umieszczonych w próżni w odległości 1 m od siebie, powoduje wzajemne oddziaływanie przewodów na siebie z siłą równą 2·10N na każdy metr długości przewodu.

Rysunek poniżej przedstawia sytuację opisaną w definicji ampera. Strzałkami oznaczono zwroty przepływu prądu w przewodach.

a) W miejscu oznaczonym na rysunku kropką zaznacz jednym z symboli ↑ → ↓ ← ⊗⊙kierunek i zwrot wektora indukcji pola magnetycznego wytwarzanego przez prąd płynący w przewodzie (1). Narysuj wektor siły, z jaką przewód (1) działa na (2).

b) W przewodach płyną prądy o natężeniu 5 A, a odległość między nimi wynosi 20 cm. Oblicz wartość siły, z jaką pierwszy przewód działa w próżni na każdy metr długości drugiego przewodu.

Zadanie 9. (SR15)

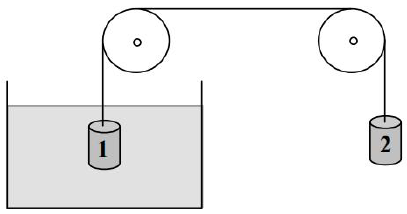
Dwa ciężarki 1 i 2 o jednakowej objętości 50

$c{m}^3$

, wykonane z różnych materiałów, zawieszono na nici przewieszonej przez dwa bloczki mogące obracać się bez tarcia.

Przytrzymując nić, zanurzono jeden z ciężarków całkowicie w wodzie o temperaturze 20 °C i gęstości 0,998

$\frac{g}{c{m}^3}$

. Po zwolnieniu nici okazało się, że układ pozostaje w spoczynku.

9.1.  

Określ relacje pomiędzy gęstościami ciężarków p 1 i p 2 oraz wody p w – wstaw właściwe znaki wybrane spośród <, >, =.

p 1 ….. p w i p 1 ….. p 2

9.2.

Masa ciężarka 2 wynosi 120 g. Oblicz masę ciężarka 1.

9.3.

Czy podgrzanie wody w naczyniu do 40 °C może wpłynąć na równowagę układu? Napisz odpowiedź i ją uzasadnij.

9.4.  

Czy równowaga jest możliwa, gdy w naczyniu zamiast wody znajduje się ciecz o innej gęstości? Wybierz i zaznacz poprawną odpowiedź.

1. Nie, w takim przypadku równowaga nie jest możliwa.
2. Tak, gdy ciecz ma mniejszą gęstość od wody, a ciężarek 1 jest częściowo zanurzony.
3. Tak, gdy ciecz ma większą gęstość od wody, a ciężarek 1 jest częściowo zanurzony.

9.5.

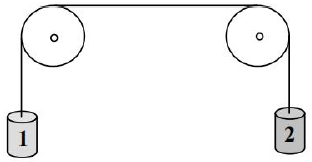
Naczynie z wodą usunięto. Masy ciężarków są równe m1 = 150 g i m2 = 120 g, a masę bloczków i nici można pominąć.

Oblicz wartość siły naciągu nici oraz wartość