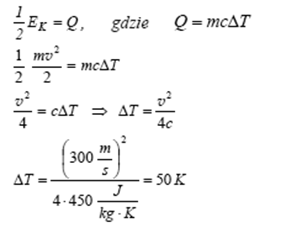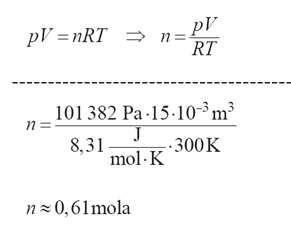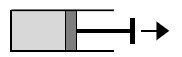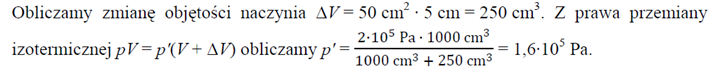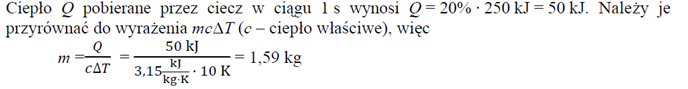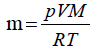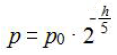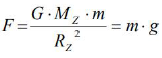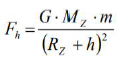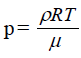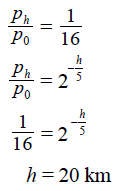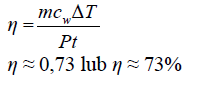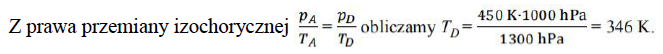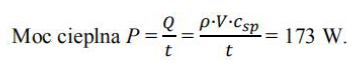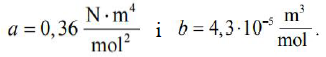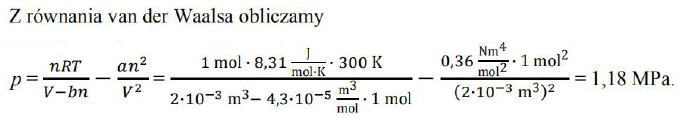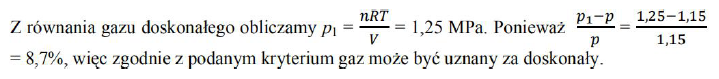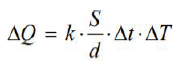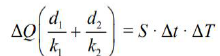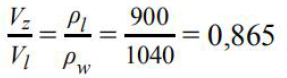Zadania maturalne z Fizyki
Temat: Termodynamika
Zadania pochodzą z oficjalnych arkuszy maturalnych CKE, które służyły przeprowadzaniu majowych egzaminów. Czteroznakowy kod zapisany przy każdym zadaniu wskazuje na jego pochodzenie: S/N – „stara”/”nowa” formuła; P/R – poziom podstawowy/rozszerzony; np. 08 – rok 2008.
Zbiór zadań maturalnych w formie arkuszy, możesz pobrać >> TUTAJ <<.
Zadanie 1. (SP05)
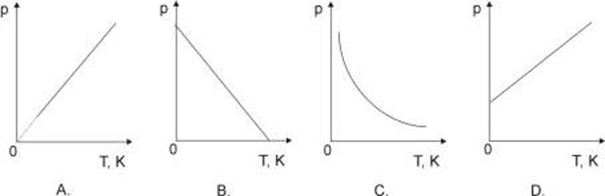
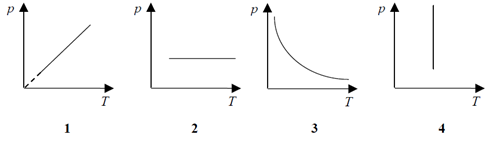
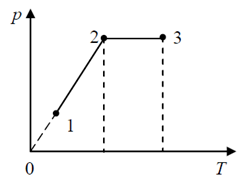
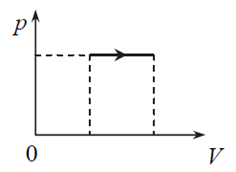
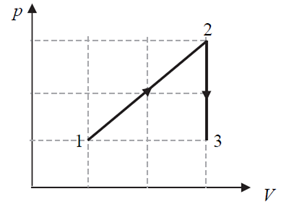
Gaz doskonały poddano przemianie, podczas której jego objętość i masa pozostawały stałe. Wskaż, który z wykresów prawidłowo przedstawia zależność zmian ciśnienia od temperatury podczas przemiany.
Zadanie 2. (SP05)
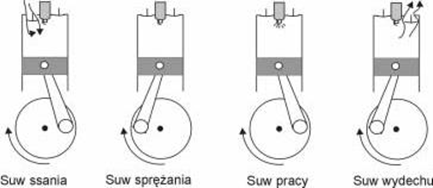
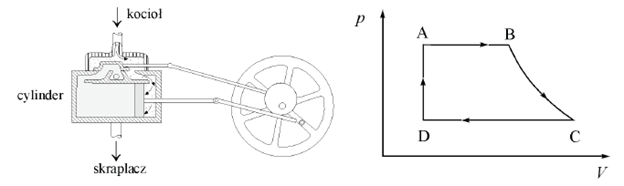
Na rysunku przedstawiony jest model budowy silnika czterosuwowego w poszczególnych etapach jego działania.
W tabeli, na następnej stronie, wypisano rodzaj zmiany ciśnienia i objętości gazu w cylindrze silnika dla poszczególnych suwów. Uzupełnij w tabeli brakujące słowa (nie zmienia się, rośnie, maleje) określające zmianę parametrów gazu.
| Suw | Ciśnienie | Objętość |
| Ssanie | Rośnie | |
| Sprężanie | Rośnie | |
| Praca | Rośnie | |
| Wydech | Nie zmienia się |
| Suw | Ciśnienie | Objętość |
| Ssanie | Nie zmienia się | Rośnie |
| Sprężanie | Rośnie | Maleje |
| Praca | Maleje | Rośnie |
| Wydech | Nie zmienia się | Maleje |
Zadanie 3. (SP05)
Przeczytaj poniżej zamieszczony tekst.
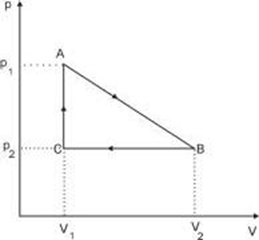
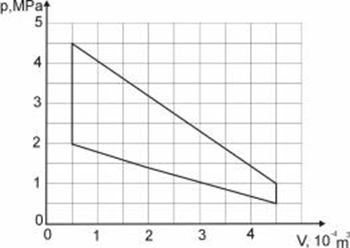
Na rysunku zaprezentowano cykl pracy pewnego silnika cieplnego.
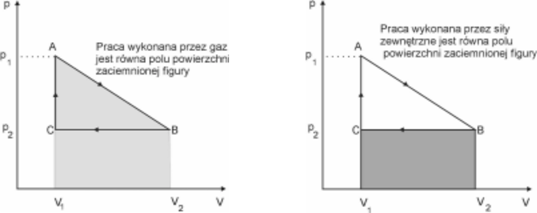
Wyliczenie sprawności takiego silnika wiąże się z wcześniejszym obliczeniem pracy użytecznej wykonanej przez gaz w czasie jednego cyklu przy wykorzystaniu wykresu zależności p(V). Wykonana praca nad gazem lub przez gaz jest równa polu powierzchni figur zakreślonych na rysunkach.
Praca użyteczna jest równa różnicy pracy wykonanej przez gaz i pracy wykonanej przez siły zewnętrzne.
Wykorzystaj zamieszczone powyżej informacje i oblicz pracę użyteczną wykonaną przez gaz w czasie jednego cyklu oraz sprawność silnika spalinowego, którego uproszczony cykl pracy przedstawiono na wykresie.
Podczas jednego cyklu pracy silnik pobiera 1200 J ciepła.
Obliczenie pracy użytecznej.
W = 600J
Obliczenie sprawności silnika.
η = ⋅100% = 50% = 0,5
Zadanie 4. (SP05)
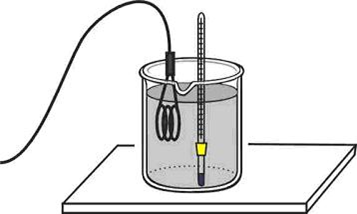
Do wody znajdującej się w zlewce włożono grzałkę elektryczną i termometr (rys.).
Po kilku minutach od momentu podłączenia grzałki do źródła prądu elektrycznego woda w warstwie powierzchniowej zaczęła wrzeć, gdy w tym samym momencie termometr mierzący temperaturę wody przy dnie zlewki wskazywał jedynie 30ûC. Wyjaśnij, dlaczego występuje tak duża różnica temperatur.
Woda jest złym przewodnikiem ciepła. Główny transport energii w wodzie odbywa się poprzez konwekcję polegającą na ruchu mas o mniejszej gęstości, a większej temperaturze do góry, a o większej gęstości i mniejszej temperaturze w dół. Dlatego woda ogrzewana przez grzałkę umieszczoną tuż pod powierzchnią wody nie jest ogrzewana jednakowo w całej objętości.
Zadanie 5. (SP05)
Celem uczniów było doświadczalne sprawdzenie, który z metali: żelazo czy aluminium jest
lepszym przewodnikiem ciepła. Uczniowie dysponowali następującymi przyrządami: prętami
o jednakowym przekroju i długości z aluminium i żelaza, do których przylepiono za pomocą
parafiny spinacze biurowe w jednakowych odległościach. Mieli również do dyspozycji palnik
gazowy, statyw, zapałki oraz stoper. Zapisz w punktach czynności wykonywane przez
uczniów podczas doświadczenia.
Zapisanie czynności wykonywanych w doświadczeniu np.:
Aby sprawdzić, który z przygotowanych metali jest lepszym przewodnikiem, należy:
- Pręt przymocować do statywu,
- Podgrzewać palnikiem jeden koniec pręta i mierzyć czas, po którym odpadną z drutu wszystkie spinacze,
- Doświadczenie powtórzyć z drugim drutem i porównać zmierzone czasy podgrzewania.
To doświadczenie może mieć zapisany inny przebieg (pomija się wykorzystanie stopera), np.:
- Przymocować pręty do statywu tak, by ich końce mogły być podgrzewane jednocześnie przez płomień palnika,
- Podgrzewać palnikiem pręty i obserwować, z którego drutu odpadnie pierwszy spinacz.
Zadanie 6. (SP06)
Stalowy pocisk, lecący z prędkością o wartości 300 m/s wbił się w hałdę piasku i ugrzązł w niej.
Oblicz maksymalny przyrost temperatury pocisku, jaki wystąpi w sytuacji opisanej w zadaniu przyjmując, że połowa energii kinetycznej pocisku została zamieniona na przyrost energii wewnętrznej pocisku. Ciepło właściwe żelaza wynosi 450 J/(kg·K).
Zadanie 7. (SP06)
Stalowy zbiornik zawiera azot pod ciśnieniem 1200 kPa. Temperatura gazu wynosi 27oC.
Zbiornik zabezpieczony jest zaworem bezpieczeństwa, który otwiera się gdy ciśnienie gazu
przekroczy 1500 kPa. Zbiornik wystawiono na działanie promieni słonecznych, w wyniku
czego temperatura gazu wzrosła do 77oC. Podaj, czy w opisanej sytuacji nastąpi otwarcie
zaworu. Odpowiedź uzasadnij, wykonując niezbędne obliczenia. Przyjmij, że objętość
zbiornika mimo ogrzania nie ulega zmianie.
Zadanie 8. (SP07)
Sprawność silnika cieplnego wynosi 20%. W ciągu 1 godziny silnik oddaje do chłodnicy 20 kJ energii. W tym czasie pobiera on z grzejnika energię cieplną o wartości
- 25 kJ.
- 40 kJ.
- 50 kJ.
- 100 kJ.
Zadanie 9. (SP07)
W cylindrze o objętości 15
znajduje się wodór. Ciśnienie wodoru jest równe 1013,82 hPa, a jego temperatura wynosi 27°C.
Oblicz liczbę moli wodoru znajdujących się w cylindrze.
Zadanie 10. (SP08)
Promienie słoneczne ogrzały szczelnie zamkniętą metalową butlę z gazem. Jeżeli pominiemy
rozszerzalność termiczną butli, to gaz w butli uległ przemianie
- izobarycznej.
- izochorycznej.
- izotermicznej.
- adiabatycznej.
Zadanie 11. (SP08)
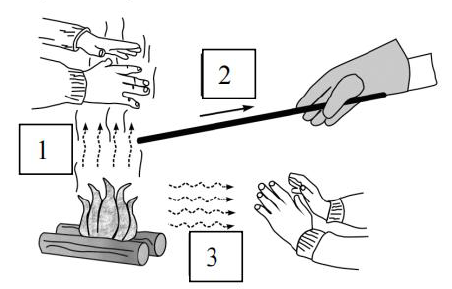
Unoszenie się w górę iskier nad płonącym ogniskiem w bezwietrzny dzień jest spowodowane zjawiskiem
- dyfuzji.
- konwekcji.
- przewodnictwa.
- promieniowania.
Zadanie 12. (SP08)
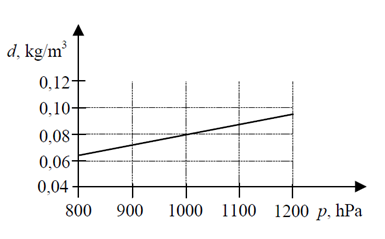
Gaz o temperaturze 27oC poddano przemianie izotermicznej. Ciśnienie początkowe gaz wynosiło 800 hPa. Wykres przedstawia zależność gęstości gazu od jego ciśnienia dla tej przemiany. Podczas przemiany masa gazu nie ulegała zmianie.
a) Oblicz masę molową tego gazu.
b) Podaj, czy w tej przemianie objętość gazu rosła, czy malała. Odpowiedź uzasadnij.
a:
b:
Zadanie 13. (SP09)
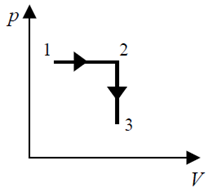
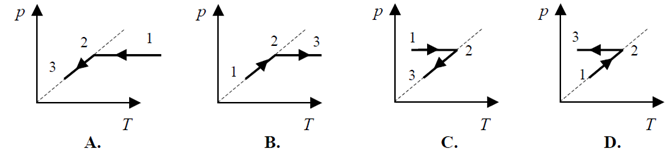
Stałą masę gazu poddano przemianie gazowej. Pierwszą zasadę termodynamiki dla tej
przemiany można zapisać: ΔU = Q. Przemianę tę poprawnie przedstawiono na wykresie
oznaczonym numerem
- 1.
- 2.
- 3.
- 4.
Zadanie 14. (SP09)
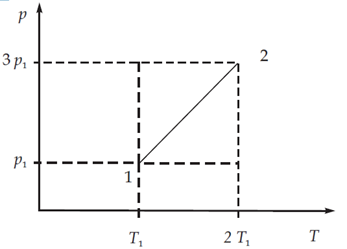
W cylindrze zamkniętym ruchomym tłokiem znajduje się 48 g gazu. Temperatura początkowa gazu wynosiła 27°C, a ciśnienie 800 hPa. Objętość gazu była równa 0,047 m3.
Gaz poddano przemianie 1 – 2, gdzie cyframi 1 i 2 oznaczono odpowiednio stan początkowy oraz końcowy gazu.
a) Ustal, jak zmieniła się (wzrosła czy zmalała) gęstość gazu w tej przemianie.
Odpowiedź uzasadnij, zapisując odpowiednie zależności.
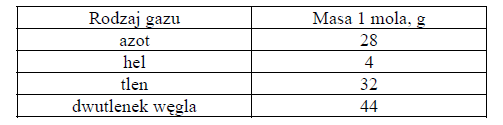
b) Ustal, który z wymienionych w tabeli gazów poddano przedstawionej powyżej przemianie.
Odpowiedź uzasadnij, wykonując konieczne obliczenia.
a):
zapisanie stwierdzenia: gęstość gazu w przemianie rosła
zapisanie uzasadnienia np.: wzrost ciśnienia gazu był trzykrotny, a temperatury dwukrotny zatem objętość malała lub zapisanie gdzie
i odpowiedni komentarz o zmianie objętości
b):
zapisanie równania: p ⋅V = n ⋅ R ⋅T i podstawienie
obliczenie masy molowej gazu (μ = 32 g)
Zdający może obliczyć liczbę moli gazu (n ≈ 1,5), a następne masę molową
prawidłowy wybór gazu z podanej tabeli: tlen
Zadanie 15. (SP10)
Poniżej przedstawiono schemat tłokowego silnika parowego oraz cykl przemian termodynamicznych związanych z jego pracą. W silniku parowym gorąca para wodna pod wysokim ciśnieniem jest wprowadzana z kotła do cylindra. Ulega tam rozprężaniu najpierw pod stałym ciśnieniem, a następnie, gdy dopływ pary jest już zamknięty, rozprężanie odbywa się bardzo szybko, bez wymiany ciepła z otoczeniem – co powoduje częściowe skroplenie się pary. Wracający tłok, przy otwartym kanale wylotowym, wypycha z cylindra do skraplacza mieszaninę wody i pary. Następnie cykl pracy silnika się powtarza.
a) Zaznacz na wykresie pracę użyteczną (wykonaną przez silnik) w jednym cyklu.
b) Zapisz nazwę przemiany jakiej podlega gaz/para na odcinku A–B.
c) W silniku parowym temperatura dostarczanej pary wynosi 227 °C, temperatura w skraplaczu jest równa 27 °C.
Oblicz teoretyczną sprawność silnika Carnota pracującego przy tych samych temperaturach, co opisany silnik parowy.
a):
zaznaczenie pola figury A – B – C – D
b):
rozprężanie przy stałym ciśnieniu (dopuszcza się zapisanie, że jest to przemiana izobaryczna)
c):
obliczenie teoretycznej sprawności silnika Carnota η = 0,4
Zadanie 16. (SP11)
Wykres obok przedstawia proces przemiany gazu doskonałego we współrzędnych p(V).
Wybierz poprawny wykres tego procesu we współrzędnych p (T)
Zadanie 17. (SP11)
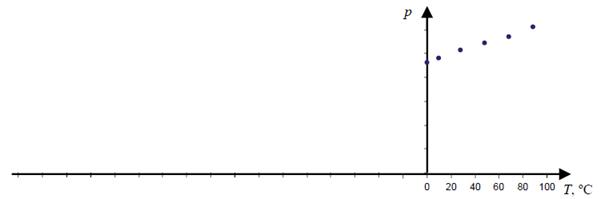
Uczniowie podgrzewali gaz w zbiorniku o stałej objętości, mierzyli ciśnienie gazu oraz jego temperaturę i zaznaczyli na poniższym wykresie punkty pomiarowe.
Nauczyciel powiedział, że taki wykres pozwala wyznaczyć temperaturę zera bezwzględnego w stopniach Celsjusza.
Opisz postępowanie prowadzące do tego celu, uzasadnij je na podstawie praw gazu doskonałego i wyznacz z wykresu przybliżoną wartość temperatury 0 K w skali Celsjusza.
W przemianie izochorycznej wielkości p i T (w skali Kelvina) są do siebie proporcjonalne, dlatego wykres przemiany jest linią prostą przecinającą oś temperatury w punkcie T = 0 K. Prowadzimy prostą przez punkty pomiarowe, przedłużając ją do przecięcia osi temperatury. Odczytujemy wartość temperatury w skali Celsjusza w punkcie przecięcia. Wynik powinien mieścić się w przedziale od –320 °C do –240 °C i być zgodny z rzeczywistym miejscem przecięcia osi na wykresie z dokładnością do 10 °C.
Zadanie 18. (SP12)
W idealnym silniku cieplnym bezwzględna temperatura grzejnika jest 5 razy wyższa od bezwzględnej temperatury chłodnicy.
Jeśli z grzejnika silnik pobrał 1000 J, to do chłodnicy oddał
- 200 J.
- 250 J.
- 750 J.
- 800 J.
Zadanie 19. (SP12)
Przynajmniej raz w roku do mieszkań w miastach przychodzi kominiarz, który sprawdza drożność przewodów kominowych przykładając do kratki wentylacyjnej wiatraczek z miernikiem szybkości obrotów.
a) Wyjaśnij, dlaczego wiatraczek działa lepiej zimą (w okresie, gdy włączone jest ogrzewanie), niż latem.
b) W którą stronę przepływa powietrze w czasie badania zimą – z przewodu kominowego do pokoju, czy odwrotnie? Napisz i uzasadnij odpowiedź.
a):
W zimie różnica temperatur jest większa, niż latem, dlatego ruch powietrza w przewodach kominowych jest silniejszy.
b):
Zimą powietrze przepływa z pokoju do przewodu kominowego z powodu różnicy ciśnień wywołanej różnicą temperatur.
Zadanie 20. (SP13)
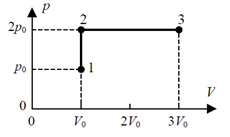
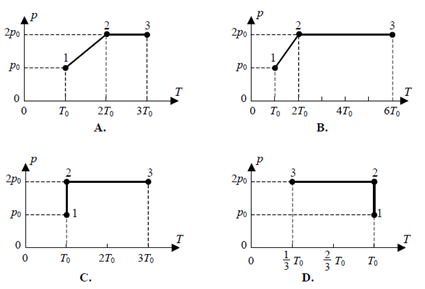
Stałą ilość gazu doskonałego poddano przemianie 1-2-3.Zmiany ciśnienia i objętości przedstawia wykres zamieszczony obok. Przemianę 1-2-3 w układzie współrzędnych p-T przedstawia wykres.
Zadanie 21. (SP13)
W naczyniu znajdował się gaz pod ciśnieniem 2·105 Pa i o temperaturze 25 °C, zamknięty tłokiem o powierzchni przekroju 50 cm2. Początkowo objętość gazu wynosiła 1000 cm3, a następnie przesunięto tłok o 5 cm w prawo, jak pokazano na rysunku. Temperatura gazu się nie zmieniła.
Oblicz ciśnienie gazu po przesunięciu tłoka.
Spośród podanych niżej zdań wybierz i podkreśl dwa poprawnie opisujące tę przemianę.
a) Energia wewnętrzna gazu wzrosła.
b) Energia wewnętrzna gazu zmalała.
c) Energia wewnętrzna gazu się nie zmieniła.
d) Gaz pobrał z otoczenia energię w postaci ciepła.
e) Gaz oddał do otoczenia energię w postaci ciepła.
f) Przemiana odbyła się bez wymiany ciepła z otoczeniem.
Podkreślenie zdań c) (Energia wewnętrzna gazu się nie zmieniła) i d) (Gaz pobrał z otoczenia energię w postaci ciepła).
Zadanie 22. (SP14)
Trzy zamknięte naczynia mają jednakową objętość. W pierwszym znajduje się 64 g tlenu,
w drugim – 84 g azotu, a w trzecim – 8 g wodoru. Temperatury tych gazów są jednakowe.
Masa jednego mola tlenu wynosi 32 g, azotu – 28 g i wodoru – 2 g. Ciśnienie gazu jest
- największe w naczyniu z tlenem.
- największe w naczyniu z azotem.
- największe w naczyniu z wodorem.
- jednakowe we wszystkich naczyniach.
Zadanie 23. (SP14)
Pewien silnik w wyniku spalania paliwa w każdej sekundzie pracy pobiera ciepło o wartości
250 kJ. W układzie chłodzącym silnika krąży ciecz, która odbiera z silnika 20% tego ciepła.
Temperatura cieczy wynosi 80 °C przy wejściu do układu chłodzącego, a 90 °C – przy
wyjściu z niego. Ciepło właściwe cieczy wynosi 3,15 kJ/kg*K. Oblicz masę cieczy
przepływającej w czasie 1 s przez układ chłodzący.
Zadanie 24. (SP14)
Początkowa objętość powietrza w pompce rowerowej wynosiła 100 cm3, jego temperatura wynosiła 20 °C, a ciśnienie było równe ciśnieniu zewnętrznemu. Podczas szybkiego sprężania zmniejsza się objętość tego powietrza i jednocześnie wzrasta jego temperatura. Przyjmujemy, że wylot pompki jest zamknięty (masa powietrza w pompce się nie zmienia).
a) Uzasadnij, korzystając z I zasady termodynamiki, dlaczego podczas szybkiego sprężania powietrza w pompce jego temperatura wzrasta.
b) W wyniku sprężania zwiększono ciśnienie w pompce do wartości 2 razy większej od ciśnienia zewnętrznego (początkowego). Oblicz objętość sprężonego powietrza, jeśli jego temperatura wzrosła o 5 °C.
a):
Sprężanie jest wykonaniem dodatniej pracy nad gazem, więc energia wewnętrzna gazu rośnie. To oznacza, że rośnie też temperatura.
b):
Zadanie 25. (NP15)
Wykres obok przedstawia zależność ciśnienia od temperatury dla pewnej masy tlenu zamkniętej w cylindrze. Spośród poniższych relacji między objętościami tlenu w stanach 1, 2 i 3 poprawne są:
- V1 = V2, V2 < V3
- V1 < V2, V2 = V3
- C. V1 = V2, V2 > V3
- V1 < V2 < V3
Zadanie 26. (NP15)
a) Dwie takie same szklanki ustawiono w ciepłej kuchni i zimnej piwnicy. Wybierz i zaznacz prawidłowe stwierdzenie A–C dotyczące ilości powietrza w obu szklankach i jego uzasadnienie I–III. Przyjmij, że ciśnienie atmosferyczne w obu pomieszczeniach jest jednakowe.
b) Temperatura w kuchni jest równa 20 °C, a ciśnienie wynosi 1000 hPa. Oblicz, ile gramów powietrza mieści się w szklance o pojemności 0,25 litra stojącej na stole w kuchni (1 litr = 1 dm3). Przyjmij średnią masę molową powietrza równą 29 g/mol.
a):
Zaznaczenie B – I.
b):
Zadanie 27. (NP16)
Przedstawiony wykres może opisywać:
- oziębianie powietrza w oponie samochodu, która zachowuje stałą objętość.
- podgrzewanie powietrza w oponie samochodu, która zachowuje stałą objętość.
- oziębianie powietrza w cylindrze, w którym tłok przesuwa się bez tarcia.
- podgrzewanie powietrza w cylindrze, w którym tłok przesuwa się bez tarcia.
Zadanie 28. (NP16)
Poniżej zapisano trzy stwierdzenia. Wpisz odpowiedni wyraz – POPRAWNE lub BŁĘDNE
– po każdym z nich.
- Nie istnieje proces termodynamiczny, którego jedynym skutkiem byłoby pobranie ciepła
od ciała chłodniejszego i przekazanie go do ciała cieplejszego. …………………………
- Możliwy jest proces termodynamiczny, którego jedynym skutkiem jest pobranie ciepła
od jednego ciała i zamiana tego ciepła na pracę mechaniczną. …………………………
- Nie jest możliwe zbudowanie urządzenia pracującego cyklicznie, które całe pobrane ciepło
zamieniałoby na pracę. ………………………….
Ocena stwierdzeń: 1. poprawne, 2. błędne, 3. poprawne.
Zadanie 29. (NP17)
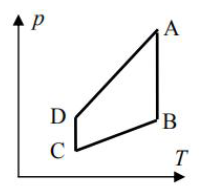
Stałą masę gazu poddano przemianom 1 → 2 → 3 przedstawionym na wykresie.
Temperatury gazu w stanach 1, 2, 3 spełniają relację
Zadanie 30. (NP17)
Gumowa piłka, nadmuchana początkowo do ciśnienia 1200 hPa i pozostawiona na plaży,
rozgrzała się od 21 °C do 42 °C. Można przyjąć, że objętość piłki nie uległa zmianie.
a) Oblicz końcowe ciśnienie powietrza w piłce.
b) Powietrze w piłce uległo jednej ze szczególnych przemian gazowych.
Uzupełnij tabelę – wpisz nazwę tej przemiany oraz odpowiednie określenia dotyczące
wielkości fizycznych wymienionych w tej tabeli.
Poniżej podano do wyboru określenia dotyczące wielkości wymienionych w tabeli.
- wzrosła/zmalała/pozostała stała,
- pobierane z otoczenia / oddawane do otoczenia / niewymieniane z otoczeniem,
- wykonywana przez gaz / wykonywana nad gazem / nie jest wykonywana.
a):
b):
Zadanie 31. (NP18)
Na wykresie obok przedstawiono cykl przemian termodynamicznych pracy pewnego silnika cieplnego. Stosunek pracy, jaką wykonuje gaz podczas rozprężania, do pracy całkowitej, którą wykonuje silnik w jednym cyklu, wynosi:
A. 1
B. 2
C. 3
D.
Zadanie 32. (NP18)
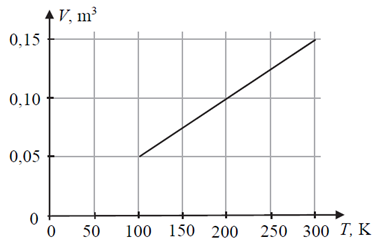
W szczelnym zbiorniku z ruchomym tłokiem znajduje się 0,2 mola gazu doskonałego. Gaz ten powoli ogrzewano, w wyniku czego jego objętość wzrosła, natomiast temperatura gazu zmieniła się od 100 K do 300 K. Zależność objętości od temperatury gazu w tej przemianie przedstawiono na wykresie obok. Masa gazu w tej przemianie się nie zmieniała.
a) Wykaż, że opisana przemiana jest izobaryczna, a ciśnienie gazu podczas tej przemiany jest równe około 3 320 Pa.
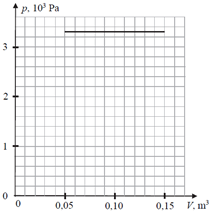
b) Narysuj wykres zależności p(V) – ciśnienia od objętości gazu – w opisanej przemianie.
c) Oblicz pracę wykonaną przez gaz podczas opisanej przemiany izobarycznej.
a):
b):
c):
Zadanie 33. (NP19)
Ustaloną masę gazu doskonałego poddano przemianie. W wyniku tej przemiany ciśnienie gazu w stanie końcowym było 2 razy mniejsze niż ciśnienie w stanie początkowym, a objętość gazu w stanie końcowym była 6 razy mniejsza niż w stanie początkowym. Temperatura gazu w stanie końcowym w porównaniu do temperatury w stanie początkowym była
- 12 razy mniejsza.
- 12 razy większa.
- 3 razy mniejsza.
- 3 razy większa.
Zadanie 34. (NP19)
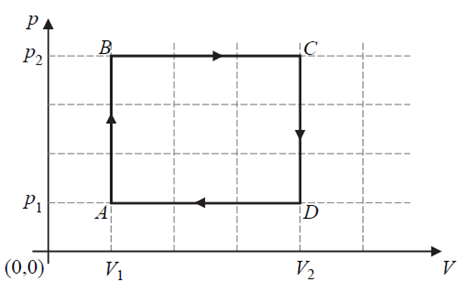
Na wykresie poniżej, w płaszczyźnie parametrów stanu (V, p) – objętości i ciśnienia, przedstawiono wykres cyklu przemian termodynamicznych ustalonej masy gazu doskonałego, które zachodzą podczas pracy pewnego silnika cieplnego. Osie na wykresie wyskalowane są liniowo.
a) Oblicz stosunek pracy całkowitej (tzw. pracy użytecznej), jaką wykonuje silnik w jednym cyklu, do pracy, którą wykonuje siła parcia gazu podczas rozprężania. Wynik liczbowy podaj w postaci ułamka zwykłego lub dziesiętnego.
b) Wyznacz temperaturę TA w stanie A, jeżeli wiadomo, że temperatura TC w stanie C wynosi 400 K.
a):
b):
Zadanie 35. (SR05)
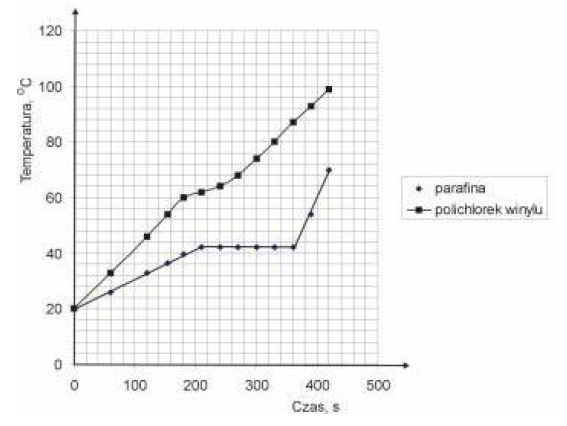
Podczas lekcji fizyki uczniowie sprawdzali, jak zachowują się podczas ogrzewania rozdrobnione substancje: parafina i polichlorek winylu. Na płycie grzejnej jednocześnie podgrzewali w zlewkach te same masy badanych substancji i mierzyli podczas ogrzewania ich temperaturę. Otrzymane wyniki uczniowie przedstawili na wykresie.
35.1
Przeanalizuj powyżej zamieszczony wykres. Zapisz, jak zachowywały się substancje podczas ogrzewania? Jaki wniosek związany z budową badanych ciał mogli uczniowie zapisać po analizie wykresu? Uzasadnij swoją odpowiedź.
35.2
Można by sądzić, że zgodnie z pierwszą zasadą termodynamiki ogrzewane ciała zwiększają swoją energię wewnętrzną , co objawia się wzrostem ich temperatury. Zapisz, czy niezmienność temperatury w przedziale od 210 do 360 sekund dla parafiny świadczy o stałej wartości energii wewnętrznej tej substancji mimo dostarczania ciepła? Wyjaśnij ten problem.
35.3
Podczas wykonywania doświadczenia ciepło dostarczane było obu substancjom równomiernie i z taką samą szybkością. Nauczyciel podał wartość ciepła właściwego zestalonej parafiny (cw= 2100 J/ (kg ⋅ o C)) i polecił uczniom, aby na podstawie wyników doświadczenia obliczyli wartość ciepła właściwego polichlorku winylu w temperaturach bliskich pokojowej.
Maciek stwierdził, że obliczenie wartości ciepła właściwego polichlorku winylu jest niemożliwe, bo nie jest znane ciepło pobrane przez polichlorek.
Jacek określił wartość ciepła właściwego polichlorku winylu na równą 1050 J/ (kg ⋅ o C)
W uzasadnieniu zapisał, że z wykresu można odczytać, iż stosunek ciepła właściwego parafiny do ciepła właściwego polichlorku winylu wynosi 2.
Zapisz, który z uczniów miał rację? Uzasadnij odpowiedź.
35.1
Obie substancje różnią się szybkością wzrostu temperatury i dlatego mają różną budowę wewnętrzną.
35.2
W tym przedziale energia wewnętrzna nie jest stała.
Na energię wewnętrzną składa się energia potencjalna (wiązań) i kinetyczna. Temperatura zależy wyłącznie od energii kinetycznej cząstek. Cała dostarczona energia zostaje zużyta na zmianę (wzrost) energii potencjalnej (wiązań), dlatego temperatura nie ulega zmianom.
Uwaga:
Można powołać się na I zasadę termodynamiki
35.3
Porównanie szybkości wzrostu temperatury obu substancji.
W czasie od 0 do 120 sekund wzrost temperatury polichlorku winylu był dwa razy większy niż w przypadku parafiny, co oznacza, że ciepło właściwe jest dwa razy mniejsze.
Zadanie 36. (SR08)
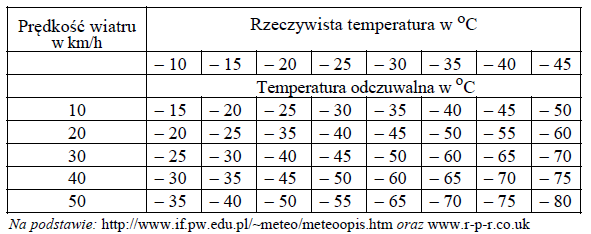
Przebywanie w mroźne dni na otwartej przestrzeni może powodować szybką utratę ciepła z organizmu, szczególnie z nieosłoniętych części ciała. Jeżeli dodatkowo wieje wiatr, wychłodzenie następuje szybciej, tak jak gdyby panowała niższa niż w rzeczywistości temperatura, zwana dalej temperaturą odczuwalną. W poniższej tabeli przedstawiono wartości rzeczywistych oraz odczuwalnych temperatur dla różnych wartości prędkości wiatru.
Na podstawie: http://www.if.pw.edu.pl/~meteo/meteoopis.htm oraz www.r-p-r.co.uk
36.1
Odczytaj z tabeli i zapisz, jaką temperaturę będą odczuwać w bezwietrzny dzień uczestniczy kuligu jadącego z prędkością o wartości 20 km/h (co jest równoważne wiatrowi wiejącemu z prędkością o wartości 20 km/h), jeżeli rzeczywista temperatura powietrza wynosi – 15oC.
Informacja do zadania 36.2 i 36.3
Za niebezpieczną temperaturę dla odkrytych części ludzkiego ciała uważa się temperaturę odczuwalną równą – 60oC i niższą.
36.2
Podaj, przy jakich wartościach prędkości wiatru rzeczywista temperatura powietrza równa – 30oC jest niebezpieczna dla odkrytych części ciała stojącego człowieka.
36.3
Analizując tabelę i wykonując oraz zapisując konieczne obliczenia, oszacuj minimalną wartość prędkości wiatru w temperaturze rzeczywistej równej – 40o C, przy której odczuwalna temperatura zaczyna być niebezpieczna dla stojącego człowieka.
36.4
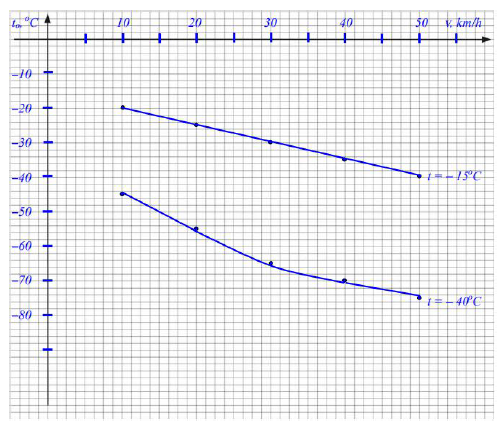
Naszkicuj w jednym układzie współrzędnych wykresy zależności temperatury odczuwalnej od wartości prędkości wiatru dla temperatury rzeczywistej – 15oC oraz – 40oC. Oznacz oba wykresy.
36.5
Przy braku wiatru temperatura odczuwalna może być nieco wyższa niż rzeczywista, jeśli człowiek nie wykonuje żadnych ruchów. Wyjaśnij tę pozorną sprzeczność. Uwzględnij fakt, że ludzkie ciało emituje ciepło.
36.1
W opisanej sytuacji temperatura odczuwalna wynosi – 25ᵒC.
36.2
W sytuacji opisanej w zadaniu temperatura powietrza będzie niebezpieczna dla odkrytych części ludzkiego ciała przy prędkości wiatru wynoszącej 40 km/h lub więcej.
36.3
Z tabeli wynika, że dla temperatury rzeczywistej równej – 40ᵒC temperatura odczuwalna staje się niebezpieczna dla stojącego człowieka przy prędkościach wiatru o wartości pomiędzy 20km/h a 30 km/h. Wartość tej prędkości można
oszacować, np.: v=
=25km/h
36.4
36.5
Ciało ludzkie emituje do otoczenia ciepło, ogrzewając otaczające człowieka powietrze. Jeśli nie ma wiatru lub człowiek nie wykonuje żadnych ruchów temperatura odczuwalna jest wyższa niż rzeczywista, gdyż w bezpośrednim otoczeniu człowieka temperatura powietrza jest wyższa.
Zadanie 37. (SR09)
Piłkę do gry w piłkę nożną napompowano azotem do ciśnienia 2000 hPa. Objętość azotu w piłce wynosiła 5,6 dm3, a jego temperatura 27oC. Masa molowa azotu jest równa 28 g/mol. Oblicz masę azotu znajdującego się w piłce. Przyjmij, że azot traktujemy jak gaz doskonały.
m = 12,6 g
Zadanie 38. (SR09)
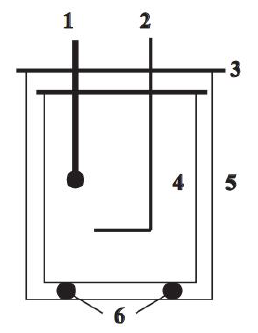
Kalorymetr to przyrząd laboratoryjny do pomiaru ciepła wydzielanego lub pobieranego podczas procesów chemicznych i fizycznych. Składa się z dwóch odizolowanych od siebie aluminiowych naczyń w kształcie walca przykrytych pokrywami.
1 – termometr, 2 – mieszadło, 3 – pokrywa, 4 – naczynie wewnętrzne,
5 – naczynie zewnętrzne, 6 – izolujące podstawki
38.1
Wyjaśnij, dlaczego kalorymetr składa się z dwóch naczyń umieszczonych jedno wewnątrz drugiego.
Informacja do zadań 38.2, 38.3 i 38.4
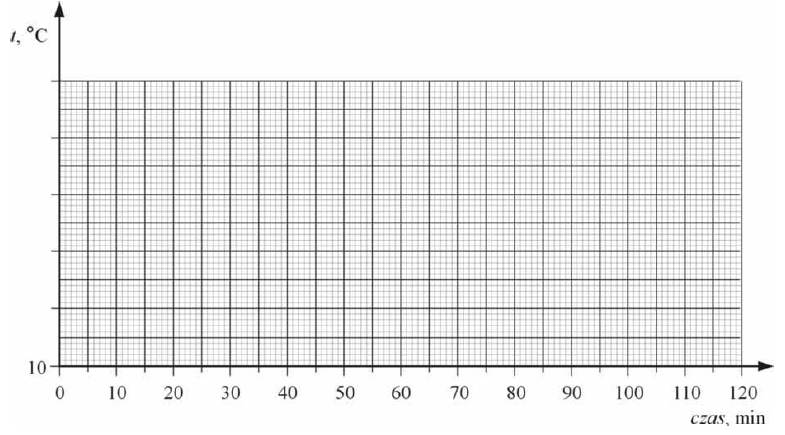
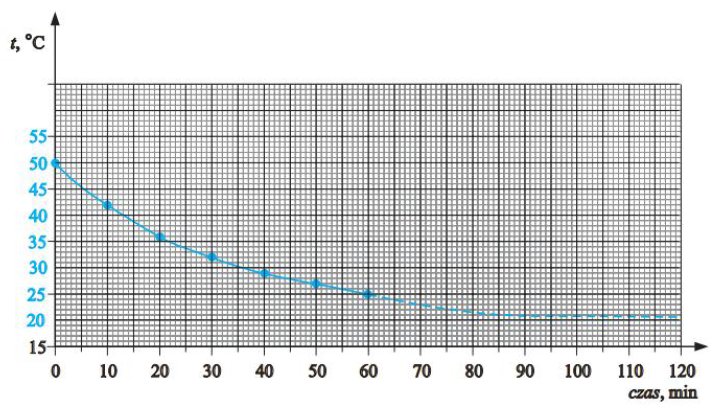
W doświadczeniu wykorzystano tylko wewnętrzne naczynie kalorymetru zamknięte pokrywą i termometr. Do naczynia wlano 0,2 kg wody o temperaturze 50oC i co 10 minut mierzono temperaturę wody. Wyniki pomiarów temperatury przedstawiono w tabeli. Temperatura otoczenia podczas pomiarów wynosiła 20oC.
| czas, w minutach | 0 | 10 | 20 | 30 | 40 | 50 | 60 |
| temperatura, w oC | 50 | 42 | 36 | 32 | 29 | 27 | 25 |
38.2
Narysuj wykres zależności temperatury wody od czasu oraz naszkicuj linią przerywaną przewidywany dalszy przebieg krzywej do końca drugiej godziny, kiedy temperatura wody praktycznie przestała się zmieniać.
38.3
Napisz, czy szybkość przepływu ciepła z naczynia do otoczenia ( Q/ t) w miarę upływu czasu rosła, malała, czy pozostawała stała.
38.4
Oblicz ciepło oddane przez wodę w czasie 10 minut od momentu rozpoczęcia pomiarów. W obliczeniach przyjmij, że ciepło właściwe wody jest równe 4200 J/kg·K.
38.5
W kolejnym doświadczeniu, aby utrzymać stałą temperaturę wody równą 90oC, umieszczono w wodzie grzałkę, którą zasilano napięciem 12 V.
Oblicz opór, jaki powinna mieć grzałka, by pracując cały czas, utrzymywała stałą temperaturę wody w naczyniu. Przyjmij, że w tych warunkach szybkość przepływu ciepła z naczynia do otoczenia wynosi 80 J/s.
38.6
| Szybkość przepływu ciepła przez warstwę materiału wyraża się wzorem: | Q | = k ⋅ S ⋅ | T | , | |
| t | d | ||||
| gdzie: | |||||
| k – współczynnik przewodnictwa cieplnego materiału warstwy, | |||||
| T – różnica temperatur po obu stronach warstwy, | |||||
| S – powierzchnia warstwy, | |||||
| d – grubość warstwy. |
Aluminiowe naczynie kalorymetru całkowicie wypełnione wodą i przykryte pokrywą ma grubość 1 mm i całkowitą powierzchnię 100 cm2. Temperatura wewnętrznej powierzchni naczynia wynosi 90oC. W tych warunkach ciepło przepływa na zewnątrz naczynia z szybkością 80 J/s.
Oblicz, z dokładnością do 0,001oC, temperaturę zewnętrznej powierzchni naczynia kalorymetru. Przyjmij, że wartość współczynnika przewodnictwa cieplnego aluminium wynosi 235 W/m·K.
38.1
Taka budowa kalorymetru zapewnia dobrą izolację termiczną dzięki warstwie powietrza znajdującej się między naczyniami.
38.2
38.3
Szybkość przepływu ciepła (ΔQ/Δt) malała
38.4
ΔT = 8ᵒC
Q = mcwΔT
Q = 6720 J
38.5
R=
R = 1,8 Ω
38.6
ΔT = 0,034ᵒC
T = 89,966ᵒC
Zadanie 39. (SR10)
Z powierzchni Ziemi wypuszczono balon stratosferyczny mający szczelną, nierozciągliwą powłokę wypełnioną wodorem.
Związek ciśnienia atmosferycznego z odległością od powierzchni Ziemi można opisać w przybliżeniu wzorem:
gdzie: p0 – ciśnienie atmosferyczne na powierzchni Ziemi, h – wysokość nad powierzchnią Ziemi wyrażona w kilometrach.
39.1
Narysuj wektory sił działających na balon podczas wznoszenia ze stałą prędkością, oznacz zapisz ich nazwy, uwzględniając siłę oporu. Zachowaj właściwe proporcje długości wektorów.
39.2
Ustal i zapisz nazwę przemiany, jakiej ulega wodór podczas wznoszenia się balonu.
39.3
Wykaż, wykonując odpowiednie przekształcenia, że dokładną wartość ciężaru balonu gdzie: RZ – promień Ziemi, g – wartość przyspieszenia ziemskiego na powierzchni Ziemi.
39.4
Wyjaśnij, dlaczego wartość siły wyporu maleje podczas wznoszenia balonu. Przyjmij, że wartość przyspieszenia ziemskiego podczas wznoszenia balonu praktycznie nie ulega zmianie.
39.5
Na maksymalnej wysokości osiągniętej przez balon gęstość powietrza wynosi około 0,1 kg/m3, a jego temperatura –55 ºC. Oblicz ciśnienie powietrza na tej wysokości. W obliczeniach powietrze potraktuj jak gaz doskonały o masie molowej równej 29 g/mol.
39.6
Oblicz, na jakiej wysokości nad powierzchnią Ziemi znajduje się balon, jeżeli ciśnienie powietrza na tej wysokości jest 16 razy mniejsze od ciśnienia na powierzchni Ziemi.
39.1
Fgr – siła grawitacji,
Fw – siła wyporu,
Fo – siła oporu

39.2
przemiana izochoryczna
39.3
na powierzchni Ziemi:
na wysokości h nad powierzchnią Ziemi:
39.4
Wartość siły wyporu maleje podczas wznoszenia balonu, ponieważ maleje gęstość powietrza.
39.5
p ≈ 6247 Pa lub p ≈ 6250 Pa lub p ≈ 6,25 kPa
39.6
Zadanie 40. (SR10)
Do czajnika elektrycznego, w którym grzałka ma moc 2000 W, wlano 0,6 kg wody o temperaturze 13 °C. Czajnik włączono do prądu elektrycznego i woda ogrzewała się aż do zagotowania przez 2 minuty i 30 sekund.
40.1
Oblicz pracę prądu elektrycznego podczas ogrzewania wody w czajniku do momentu jej zagotowania.
40.2
Oblicz sprawność ogrzewania wody w czajniku. W obliczeniach przyjmij, że ciepło właściwe wody jest równe 4200
i nie zmienia się podczas ogrzewania wody.
Informacja do zadań 40.3, 40.4 i 40.5
W poniższej tabeli przedstawiono wyniki pomiarów wykonanych podczas doświadczenia z czajnikiem elektrycznym. Temperatura początkowa wody w czajniku przed podłączeniem go do prądu była za każdym razem zawsze taka sama i wynosiła 13 °C.
40.3
Przeanalizuj dane w tabeli i zapisz wniosek dotyczący związku względnej straty energii z masą zagotowywanej wody.
40.4
Narysuj wykres zależności sprawności ogrzewania wody w czajniku od jej masy.
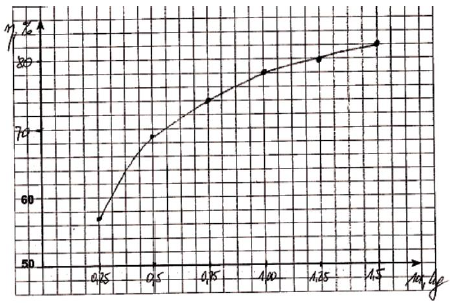
40.5
Wykaż, korzystając z danych w tabeli (lub zawartych na wykresie), że bezwzględne straty dostarczonej do czajnika energii rosną wraz z masą ogrzewanej wody.
40.1
W = P ⋅t
W = 300 kJ
40.2
40.3
Im większa masa wody tym względne straty energii są mniejsze.
40.4
40.5
wyznaczenie bezwzględnych strat energii korzystając z zależności:
ΔEi = (1/ηi – 1)·mi·c·ΔT
Porównanie przynajmniej dla dwóch mas wody wartości bezwzględnych strat energii i wykazanie, że teza postawiona w zadaniu jest prawdziwa.
Zadanie 41. (SR11)
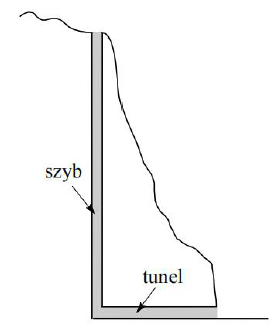
W zboczu góry rozpoczęto budowę kopalni – wykonano poziomy tunel i pionowy szyb wentylacyjny (rys.).
41.1
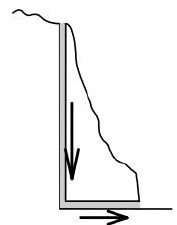
Ustal i zaznacz strzałkami na rysunku, w którą stronę odbywa się ruch powietrza w tunelu i szybie w lecie, jeżeli na zewnątrz góry temperatura jest równa 25 °C, a wewnątrz tunelu i szybu 10 °C. Podaj krótkie uzasadnienie.
41.2
Pod ciśnieniem p i w temperaturze 25 ºC gęstość powietrza jest równa 1,20 kg/m3. Traktując powietrze jako gaz doskonały, oblicz jego gęstość pod tym samym ciśnieniem p i w temperaturze 10 ºC.
41.3
W tunelu zainstalowano szczelną zaporę przeciwpożarową i przepływ powietrza ustał. Wysokość szybu jest równa 200 m, a średnia gęstość powietrza w szybie wynosi 1,3 kg/m3. Oblicz ciśnienie słupa powietrza w szybie (różnicę między ciśnieniem na poziomie tunelu a ciśnieniem przy górnym wylocie szybu).
Oblicz ciśnienie słupa powietrza atmosferycznego o wysokości 200 m na zewnątrz góry. Średnia gęstość powietrza na zewnątrz wynosi 1,2 kg/m3.
Powierzchnia zapory wynosi 7 m2. Oblicz wypadkową siłę parcia powietrza działającą na zaporę z obu stron.
41.1
W niższej temperaturze gęstość powietrza jest większa i powietrze opada.
41.2
Z równania Clapeyrona lub prawa przemiany izobarycznej wyprowadzamy zależność ρ ~ 1/T
lub proporcję
Do wzoru ρ2 = ρ1
podstawiamy dane ρ1 oraz T1 = 298 K, T2 = 283 K i otrzymujemy ρ2 = 1,26 kg/m
41.3
Ze wzoru p = ρgh otrzymujemy ci śnienie słupa powietrza w szybie p1 = 2550 Pa i ciśnienie słupa na zewnątrz p2 = 2350 Pa. Ze wzoru F = (p1 – p2)S obliczamy F = 1400 N.
Zadanie 42. (SR12)
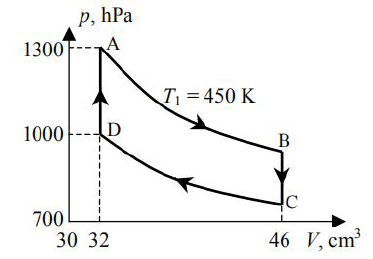
Istnieje wiele typów silników cieplnych. Silnik Stirlinga wyróżnia się tym, że wewnątrz silnika nie występuje spalanie paliwa, a czynnikiem roboczym (gazem podlegającym przemianom) jest powietrze. Zaletą silnika Stirlinga jest niski poziom hałasu, niski poziom emisji szkodliwych składników i wysoka sprawność cieplna. Silnik składa się z cylindra podgrzewanego przez palnik i połączonego z nim zimnego cylindra chłodzonego powietrzem. Obok przedstawiono uproszczony cykl pracy tego silnika w układzie zmiennych p–V. W przemianach A→B i C→D temperatura się nie zmienia.
42.1
Oblicz temperaturę powietrza w punkcie D cyklu.
42.2
Oblicz ciśnienie powietrza w punkcie B cyklu.
42.3
W palniku spalany jest spirytus. Oblicz moc cieplną palnika, który w ciągu godziny spala 30 cm3 paliwa o gęstości 0,83 g/cm3 i cieple spalania 25 kJ/g. Wynik podaj w watach.
42.4
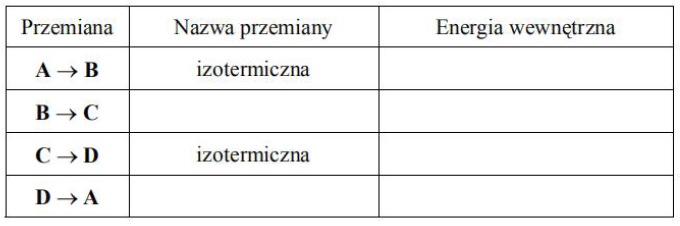
Uzupełnij poniższą tabelę, wpisując nazwy przemian B→C i D→A oraz rodzaj zmiany energii wewnętrznej gazu dla wszystkich przemian (rośnie lub maleje lub nie zmienia się).
42.5
Naszkicuj cykl pracy silnika w układzie zmiennych p–T. Oznacz poszczególne etapy cyklu. Na wykresie nie nanoś wartości liczbowych.
42.6
a) Oblicz liczbę moli gazu, który podlegał opisanym przemianom.
b) Przyjmując temperaturę w punkcie D równą 340 K oraz ciepło molowe powietrza przy stałej objętości CV = 21 , oblicz ciepło dostarczone do silnika podczas przemiany D→A.
42.1
42.2
42.3
42.4
Poprawna odpowiedź:
A → B: U nie zmienia się
B → C: przemiana izochoryczna, U maleje
C → D: U nie zmienia się
D → A: przemiana izochoryczna, U rośnie
42.5
42.6
Zadanie 43. (SR13)
Gazy rzeczywiste w pewnym zakresie parametrów można traktować jak gaz doskonały (idealny). Temperatura gazu doskonałego T jest proporcjonalna do średniej energii kinetycznej ruchu postępowego jego cząsteczek. Dla gazu doskonałego spełnione jest równanie Clapeyrona.
43.1
Uzupełnij zdania, podkreślając poprawne stwierdzenia, tak aby opisywały gaz według modelu gazu doskonałego.
- Rozmiary cząsteczek i zajmowaną przez nie objętość uwzględniamy / pomijamy.
- Cząsteczki gazu oddziałują ze sobą tylko podczas zderzeń / także na odległość.
- Zderzenia cząsteczek ze sobą i ściankami naczynia są sprężyste / niesprężyste.
43.2
Powietrze jest mieszaniną gazów, m.in. tlenu O2 (masa molowa 32 g/mol), azotu N2 (masa molowa 28 g/mol) i argonu Ar (masa molowa 40 g/mol). Określ zależność między średnimi prędkościami tych cząsteczek, wpisując w lukach znaki wybrane spośród =, > i <.
Przez średnią prędkość rozumiemy tu średnią wartość wektora prędkości.
vargonu … vtlenu … vazotu
43.3
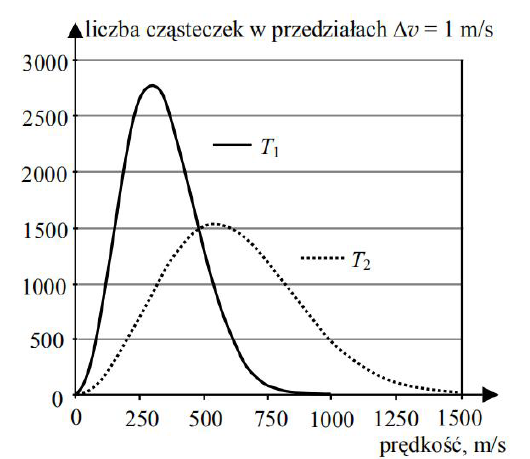
Podane wyżej wykresy przedstawiają tzw. rozkład Maxwella.
Na osi pionowej odłożono liczbę cząsteczek gazu, których wartości prędkości leżą w przedziale od v do v + v, dla szerokości przedziału v równej 1 m/s. Wykresy wykonano dla jednego miliona cząsteczek gazu o temperaturze T1 i o temperaturze T2.
Podaj, która z temperatur T1 i T2 jest wyższa. Uzasadnij odpowiedź.
43.4
Jeden mol gazu doskonałego o temperaturze początkowej t1 = 27 °C i ciśnieniu początkowym p1 = 1000 hPa ogrzano izobarycznie o 300 °C, a następnie izochorycznie o kolejne 300 °C. Oblicz końcowe ciśnienie gazu p3.
Informacja do zadań 43.5 i 43.6
Dla gazu rzeczywistego zamiast równania Clapeyrona stosuje się równanie van der Waalsa, które dla n moli gazu ma postać 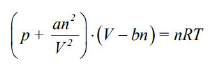
43.5
Korzystając z równania van der Waalsa, oblicz ciśnienie 1 mola dwutlenku węgla o temperaturze 300 K, zamkniętego w zbiorniku o objętości 2 dm3.
43.6
Przyjmijmy, że gaz stosuje się do modelu gazu doskonałego, gdy ciśnienie gazu obliczone z równania Clapeyrona nie różni się od ciśnienia rzeczywistego o więcej niż 10%. Dla 1 mola pewnego gazu rzeczywistego o temperaturze 300 K zamkniętego w zbiorniku o objętości 2 dm3 ciśnienie jest równe 1,15 MPa. Wykonaj niezbędne obliczenia i ustal, czy ten gaz może być traktowany jak gaz doskonały.
43.1
Podkreślenia pomijamy, tylko podczas zderzeń, sprężyste.
43.2
Wpisanie dwóch symboli <: vargonu < vtlenu < vazotu.
43.3
Temperatura T2 jest wyższa, ponieważ w tej temperaturze cząsteczki mają większą średnią prędkość (co można odczytać z wykresu).
43.4
Wartości temperatur w skali Kelvina wynoszą T1 = 300 K, T2 = 600 K i T3 = 900 K. Stosując do przemiany 2-3 prawo przemiany izochorycznej, otrzymujemy p3 =
p1 =1,5 p1 = 1500 hPa.
43.5
43.6
Zadanie 44. (SR13)
44.1
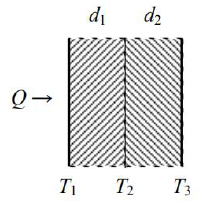
Wpisz właściwe nazwy procesów cieplnych oznaczonych na rysunku numerami 1–3.
- ……………………………………………………..
- ……………………………………………………..
- ……………………………………………………..
Informacja do zadań 44.2 – 44.5
Ilość ciepła przepływająca w czasie Δt przez ścianę o grubości d i powierzchni S, gdy różnica temperatur między powierzchniami ściany jest równa ΔT, można opisać wzorem
gdzie k jest współczynnikiem cieplnego przewodnictwa właściwego, zależnym od materiału ściany. Zakładamy, że temperatura każdego punktu ściany pozostaje stała w czasie.
44.2
Wyraź jednostkę współczynnika k występującego we wzorze (*) w jednostkach podstawowych układu SI.
44.3
Wyjaśnij, odwołując się do mikroskopowych własności substancji, dlaczego materiały o porowatej budowie (np.: styropian, gąbka lub puch) są złymi przewodnikami ciepła.
44.4
Ściana ma powierzchnię 3 m × 5 m i grubość 30 cm, a wykonana jest z cegły ceramicznej, dla której współczynnik cieplnego przewodnictwa właściwego jest równy 0,77 W/(m·K). Oblicz moc cieplną (w watach) wyrażającą szybkość przepływu ciepła przez tę ścianę, gdy wewnątrz budynku temperatura jest równa +20 °C, a na zewnątrz jest równa –10 °C.
44.5
Ściana składa się z dwóch warstw o grubościach d1 i d2 wykonanych z materiałów o współczynnikach cieplnego przewodnictwa właściwego równych odpowiednio k1 i k2, a różnica temperatur między zewnętrznymi powierzchniami wynosi ΔT = T1 – T3. Wykaż, że prawdziwa jest zależność
Zadanie 45. (NR15)
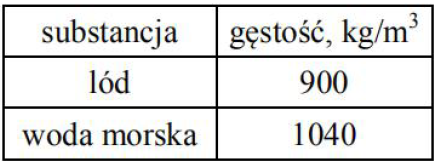
Wykorzystując dane z tabeli, oblicz, jaka część objętości góry lodowej wystaje ponad powierzchnię wody.
Na górę działają dwie równoważące się siły: siła ciężkości Fg = ρlVl g (gdzie ρl i Vl to gęstość i objętość lodu) i siła wyporu Fw. Zgodnie z prawem Archimedesa Fw = ρwVz g, gdzie ρw jest gęstością wody, a Vz – objętością części zanurzonej. Stąd
Skoro objętość części zanurzonej jest równa 0,865 całkowitej objętości lodu, to objętość części wynurzonej jest równa 1 – 0,865 = 0,135 (13,5%) objętości góry.
Zadanie 46. (NR15)
Wymień trzy różne zjawiska powodujące stygnięcie otwartego naczynia z gorącą wodą.
Zjawiskami tymi są przewodnictwo cieplne, konwekcja (lub konwekcja w powietrzu), parowanie wody i promieniowanie.
Uwaga. Nie uznaje się m.in. odpowiedzi: oddawanie ciepła do naczynia (gdyż pytanie dotyczyło stygnięcia naczynia z wodą, a nie stygnięcia samej wody), konwekcja w wodzie (wymiana ciepła wewnątrz naczynia nie jest odpływem ciepła na zewnątrz), a także „występowanie różnicy temperatur” (ponieważ nie jest to nazwa zjawiska fizycznego).