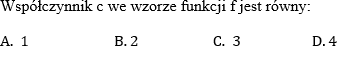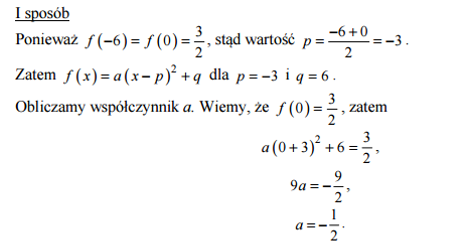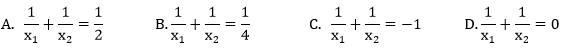Zadania maturalne z Matematyki
Tematyka: funkcje kwadratowe, wzory Vieta.
Zadania pochodzą z oficjalnych arkuszy maturalnych CKE, które służyły przeprowadzaniu majowych egzaminów. Czteroznakowy kod zapisany przy każdym zadaniu wskazuje na jego pochodzenie: S/N – „stara”/”nowa” formuła; P/R – poziom podstawowy/rozszerzony; np. 08 – rok 2008.
Zbiór zadań maturalnych w formie arkuszy, możesz pobrać >> TUTAJ <<.
Zadanie 1. (NP15)
Funkcja kwadratowa określona jest wzorem f(x)=x2+x+c. Jeśli f(3)=4, to:
Zadanie 2. (NP15)
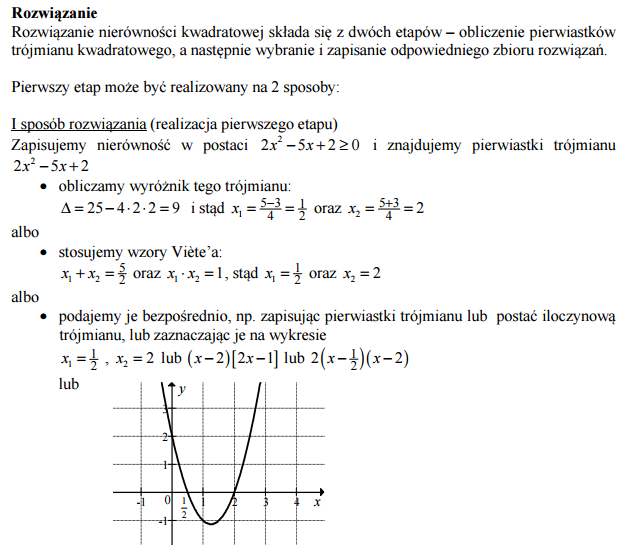
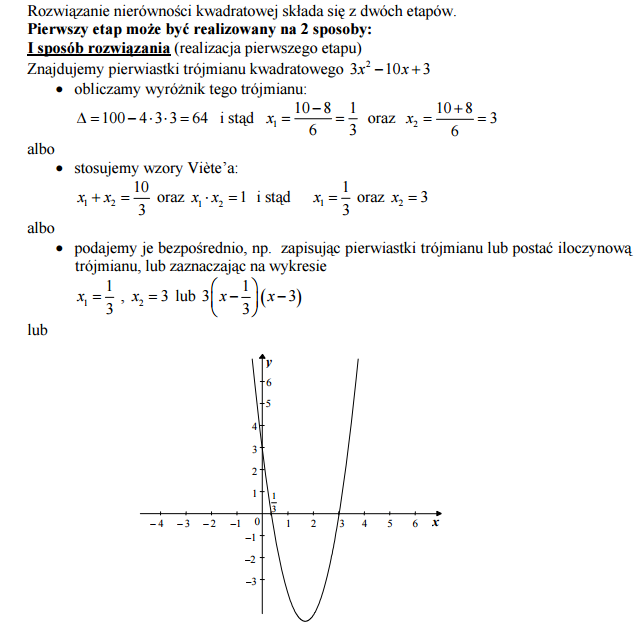
Rozwiąż nierówność
Zadanie 3. (NP15)
Oblicz najmniejszą i największą wartość funkcji kwadratowej w przedziale <0,4>.
Zadanie 4. (NP16)
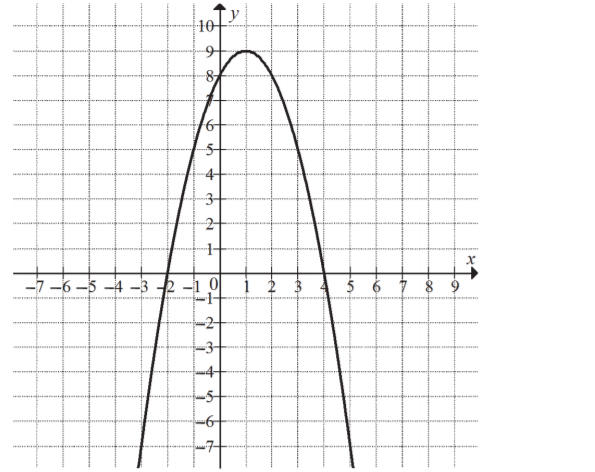
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej f. Wierzchołkiem tej paraboli jest punkt W=(1,9). Liczby −2 i 4 to miejsca zerowe funkcji f.
Zadanie 5. (NP16)
Najmniejsza wartość funkcji f w przedziale ⟨−1;2⟩ jest równa:
Zadanie 6. (NP16)
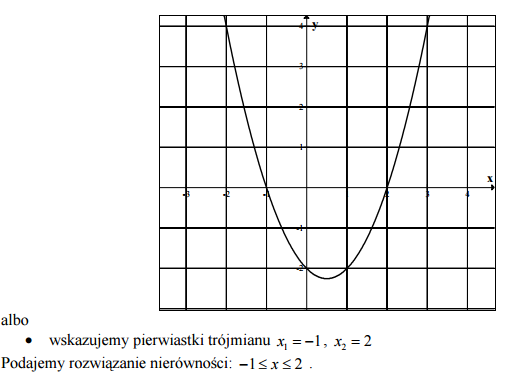
Rozwiąż nierówność .
Zadanie 7. (NP17)
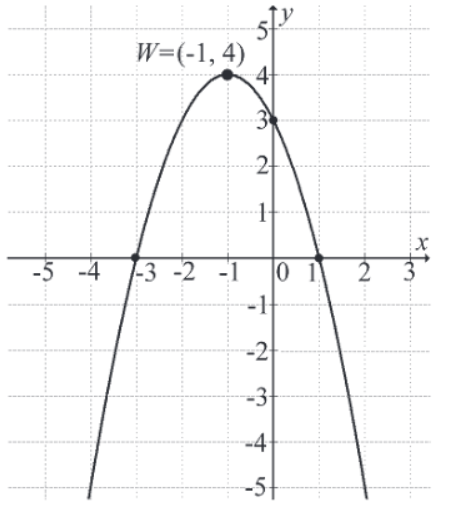
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej f(x)=ax2+bx+c, o miejscach zerowych: −3 i 1.
Zadanie 8. (NP17)
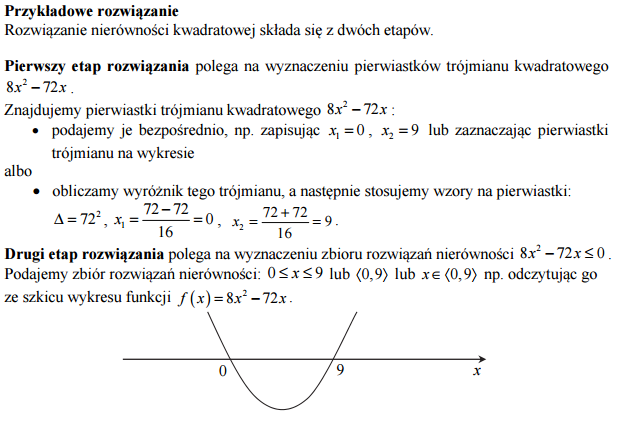
Rozwiąż nierówność 8x2−72x≤0.
Zadanie 9. (NP17)
Funkcja kwadratowa f jest określona dla wszystkich liczb rzeczywistych x wzorem f(x)=ax2+bx+c. Największa wartość funkcji f jest równa 6 oraz f(−6)=f(0)= . Oblicz wartość współczynnika a.
Zadanie 10. (NP18)
Funkcja kwadratowa jest określona wzorem f(x)=−2(x+3)(x−5). Liczby x1, x2 są różnymi miejscami zerowymi funkcji f. Zatem:
Zadanie 11. (NP18)
Wykresem funkcji kwadratowej f(x)=x2−6x−3 jest parabola, której wierzchołkiem jest punkt o współrzędnych:
Zadanie 12. (NP18)
Rozwiąż nierówność 2x2−3x>5.
Zadanie 13. (SP15)
Rozwiąż nierówność 2x2−4x>x-2.
Zadanie 14. (SP16)
Rozwiąż nierówność 2x2+5x-3>0.
Zadanie 16. (SP14)
Pierwiastki x1,x2 równania 2(x+2)(x−2)=0 spełniają warunek f.
Zadanie 17. (SP14)
Wykresem funkcji kwadratowej f(x)=2x2+bx+c jest parabola, której wierzchołkiem jest punkt W=(4,0). Oblicz wartości współczynników b i c.
Zadanie 18. (SP13)
Wierzchołkiem paraboli o równaniu y=−3(x−2)2+4 jest punkt o współrzędnych:
Zadanie 19. (SP13)
Dla każdej liczby rzeczywistej x, wyrażenie 4x2−12x+9 jest równe:
Zadanie 20. (SP13)
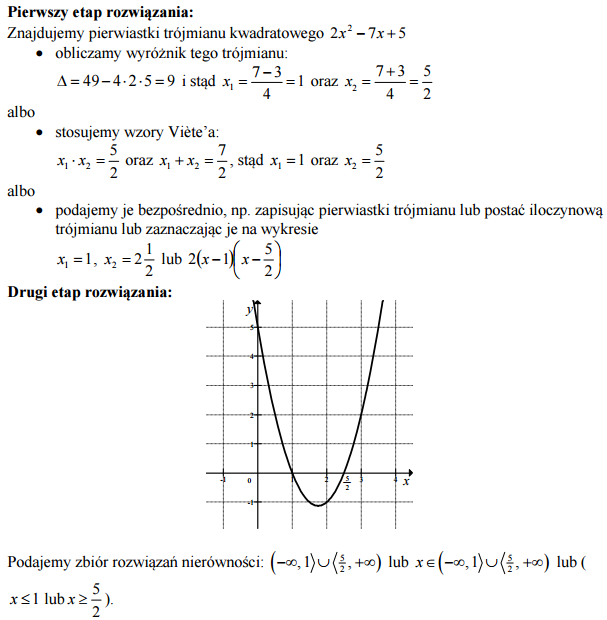
Rozwiąż nierówność 2x2−7x+5≥0.
Zadanie 21. (SP13)
Liczby x1,x2 są różnymi rozwiązaniami równania 2x2+3x−7=0. Suma x1+x2 jest równa:
Zadanie 22. (SP12)
Miejscami zerowymi funkcji kwadratowej y=−3(x−7)(x+2) są:
Zadanie 23. (SP12)
Rozwiąż nierówność x2+8x+15>0.
Zadanie 24. (SP11)
Wskaż, który zbiór przedstawiony na osi liczbowej jest zbiorem liczb spełniających jednocześnie następujące nierówności: 3(x−1)(x−5)≤0 i x>1.
Zadanie 25. (SP11)
Rozwiąż nierówność 3x2-10x+30.
Zadanie 26. (SP10)
Do zbioru rozwiązań nierówności (x−2)(x+3)<0 należy liczba:
Zadanie 27. (SP10)
Wykresem funkcji kwadratowej f(x)=−3x2+3 jest parabola o wierzchołku w punkcie:
Zadanie 28. (SP10)
Rozwiąż nierówność x2−x-2≤0.
Zadanie 29. (SP09)
Wykres funkcji f danej wzorem f(x) -2 x2 przesunięto wzdłuż osi OX o 3 jednostki w prawo i wzdłuż osi OY o 8 jednostek w górę, powstał wykres funkcji g.
a) Rozwiąż nierówność f(x) + 5 <3x
b) Podaj zbiór wartości funkcji g
c) Funkcja g określona wzorem g(x) = -2 x2 +bx +c . Oblicz b i c.
a)
b)
c)
Zadanie 30. (SP08)
Oblicz najmniejszą i największą wartość funkcji kwadratowej f (x ) = (2x + 1)(x − 2) w przedziale ⟨− 2,2⟩ .
Zadanie 31. (SP07)
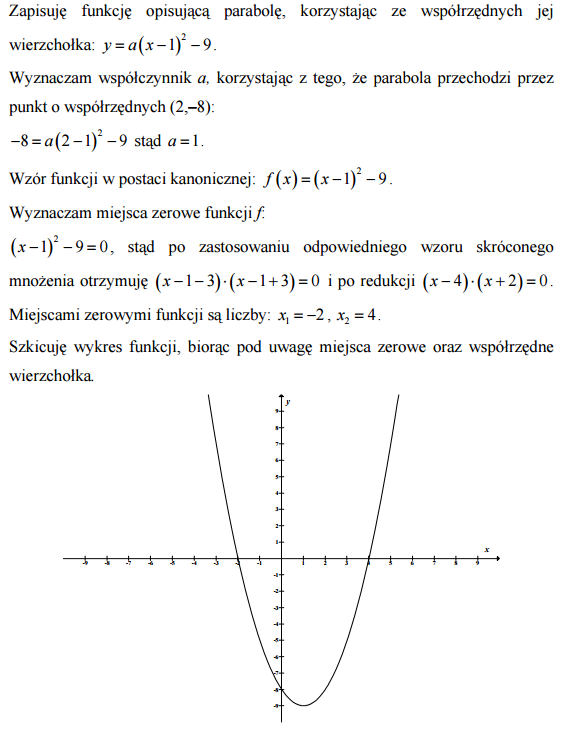
Znajdź wzór funkcji kwadratowej y = f (x) , której wykresem jest parabola o wierzchołku (1,− 9) przechodząca przez punkt o współrzędnych (2,− 8) . Otrzymaną funkcję przedstaw w postaci kanonicznej. Oblicz jej miejsca zerowe i naszkicuj wykres.
Zadanie 32. (SP06)
Dana jest funkcja f(x)=-x2+6x-5 .
a) Naszkicuj wykres funkcji f i podaj jej zbiór wartości.
b) Podaj rozwiązanie nierówności f (x) ≥0 .