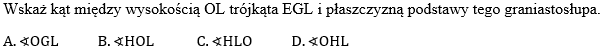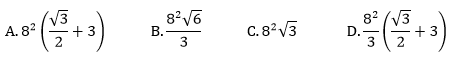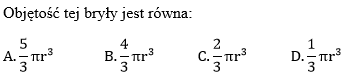Zadania maturalne z Matematyki
Tematyka: geometria przestrzenna: graniastosłupy, prostopadłościany, sześcian, walec, ostrosłup, stożek, kula.
Zadania pochodzą z oficjalnych arkuszy maturalnych CKE, które służyły przeprowadzaniu majowych egzaminów. Czteroznakowy kod zapisany przy każdym zadaniu wskazuje na jego pochodzenie: S/N – „stara”/”nowa” formuła; P/R – poziom podstawowy/rozszerzony; np. 08 – rok 2008.
Zbiór zadań maturalnych w formie arkuszy, możesz pobrać >> TUTAJ <<.
Zadanie 1. (NP15)
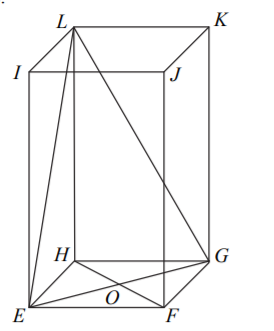
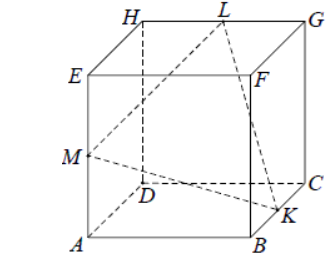
W graniastosłupie prawidłowym czworokątnym EFGHIJKL wierzchołki E,G,L połączono odcinkami (tak jak na rysunku).
Zadanie 2. (NP15)
Przekrojem osiowym stożka jest trójkąt równoboczny o boku długości 6. Objętość tego stożka jest równa:
Zadanie 3. (NP15)
Każda krawędź graniastosłupa prawidłowego trójkątnego ma długość równą 8. Pole powierzchni całkowitej tego graniastosłupa jest równe:
Zadanie 4. (NP15)
Wysokość graniastosłupa prawidłowego czworokątnego jest równa 16. Przekątna graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem, którego cosinus jest równy . Oblicz pole powierzchni całkowitej tego graniastosłupa.
Zadanie 5. (NP16)
Kąt rozwarcia stożka ma miarę 120 stopni a tworząca tego stożka ma długość 4. Objętość tego stożka jest równa:
Zadanie 6. (NP16)
Przekątna podstawy graniastosłupa prawidłowego czworokątnego jest dwa razy dłuższa od wysokości graniastosłupa. Graniastosłup przecięto płaszczyzną przechodzącą przez przekątną podstawy i jeden wierzchołek drugiej podstawy (patrz rysunek).
Zadanie 7. (NP16)
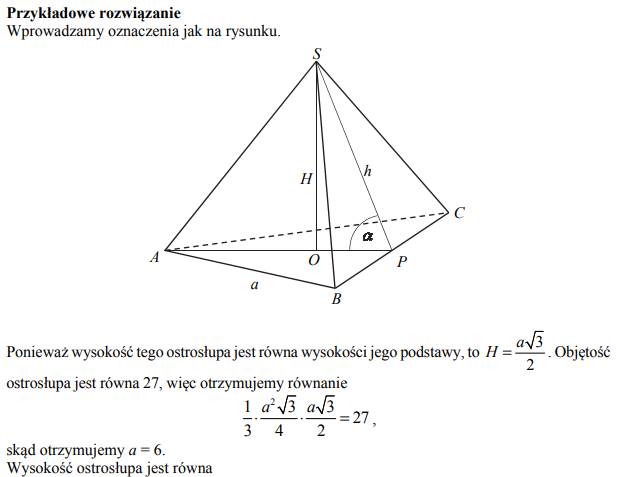
Podstawą ostrosłupa prawidłowego trójkątnego ABCS jest trójkąt równoboczny ABC. Wysokość SO tego ostrosłupa jest równa wysokości jego podstawy. Objętość tego ostrosłupa jest równa 27. Oblicz pole powierzchni bocznej ostrosłupa ABCS oraz cosinus kąta, jaki tworzą wysokość ściany bocznej i płaszczyzna podstawy ostrosłupa.
Zadanie 8. (NP17)
Pole powierzchni całkowitej graniastosłupa prawidłowego czworokątnego, w którym wysokość jest 3 razy dłuższa od krawędzi podstawy, jest równe 140. Zatem krawędź podstawy tego graniastosłupa jest równa:
Zadanie 9. (NP17)
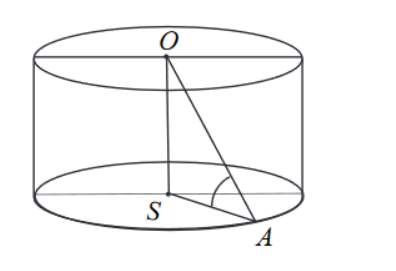
Promień AS podstawy walca jest równy wysokości OS tego walca. Sinus kąta OAS (zobacz rysunek) jest równy:
Zadanie 10. (NP17)
Dany jest stożek o wysokości 4 i średnicy podstawy 12. Objętość tego stożka jest równa:
Zadanie 11. (NP17)
W ostrosłupie prawidłowym trójkątnym wysokość ściany bocznej prostopadła do krawędzi podstawy ostrosłupa jest równa , a pole powierzchni bocznej tego ostrosłupa jest równe
. Oblicz objętość tego ostrosłupa.
Zadanie 12. (NP18)
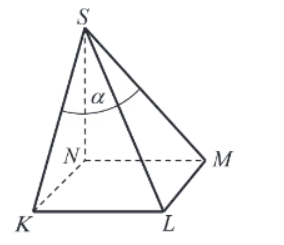
Podstawą ostrosłupa jest kwadrat KLMN o boku długości 4. Wysokością tego ostrosłupa jest krawędź NS, a jej długość też jest równa 4 (zobacz rysunek).
Zadanie 13. (NP18)
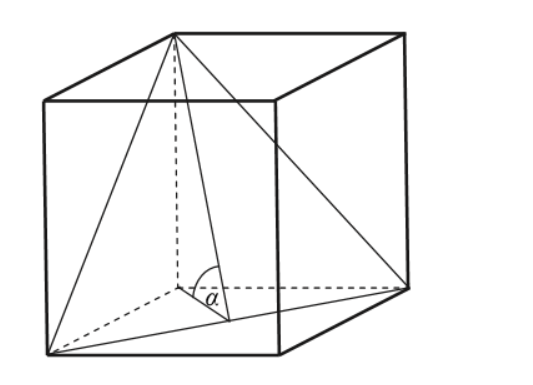
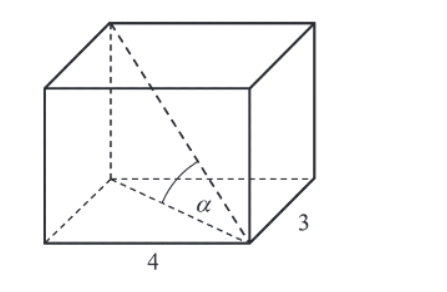
Podstawą graniastosłupa prostego jest prostokąt o bokach długości 3 i 4. Kąt α, jaki przekątna tego graniastosłupa tworzy z jego podstawą, jest równy (zobacz rysunek).
Zadanie 14. (NP18)
Na rysunku przedstawiono bryłę zbudowaną z walca i półkuli. Wysokość walca jest równa r i jest taka sama jak promień półkuli oraz taka sama jak promień podstawy walca.
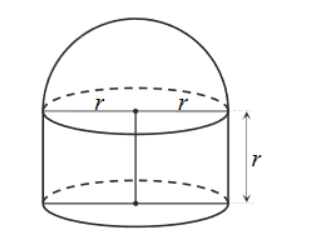
Zadanie 15. (NP18)
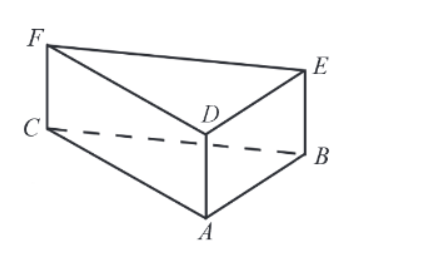
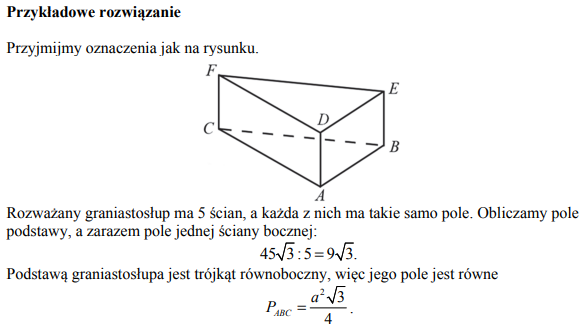
Dany jest graniastosłup prawidłowy trójkątny (zobacz rysunek). Pole powierzchni całkowitej tego graniastosłupa jest równe .Pole podstawy graniastosłupa jest równe polu jednej ściany bocznej. Oblicz objętość tego graniastosłupa.
Zadanie 16. (SP15)
Przekątna ściany sześcianu ma długość 2. Pole powierzchni całkowitej tego sześcianu jest równe:
Zadanie 17. (SP15)
Kula o promieniu 5 cm i stożek o promieniu podstawy 10 cm mają równe objętości. Wysokość stożka jest równa:
Zadanie 18. (SP14)
Jeżeli ostrosłup ma 10 krawędzi, to liczba ścian bocznych jest równa:
Zadanie 19. (SP14)
Stożek i walec mają takie same podstawy i równe pola powierzchni bocznych. Wtedy tworząca stożka jest:
A. sześć razy dłuższa od wysokości walca
B. trzy razy dłuższa od wysokości walca
C. dwa razy dłuższa od wysokości walca
D. równa wysokości walca.
Zadanie 20. (SP14)
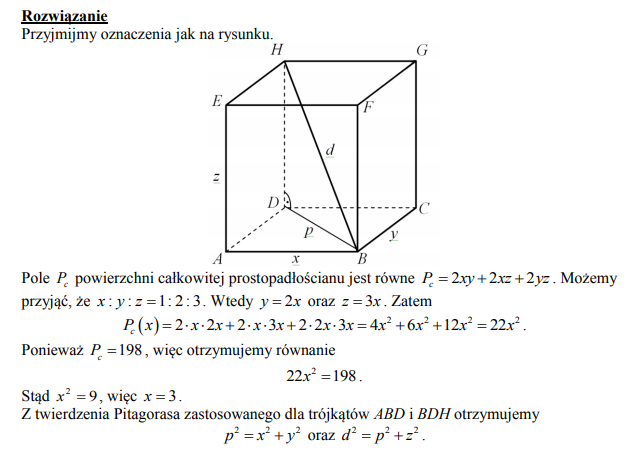
Pole powierzchni całkowitej prostopadłościanu jest równe 198. Stosunki długości krawędzi prostopadłościanu wychodzących z tego samego wierzchołka prostopadłościanu to 1:2:3. Oblicz długość przekątnej tego prostopadłościanu.
Zadanie 21. (SP13)
Liczba wszystkich krawędzi graniastosłupa jest o 10 większa od liczby wszystkich jego ścian bocznych. Stąd wynika, że podstawą tego graniastosłupa jest:
A. czworokąt B pięciokąt C. sześciokąt D. dziesięciokąt
Zadanie 22. (SP13)
Pole powierzchni bocznej stożka o wysokości 4 i promieniu podstawy 3 jest równe:
Zadanie 23. (SP13)
Objętość graniastosłupa prawidłowego trójkątnego o wysokości 7 jest równa . Długość krawędzi podstawy tego graniastosłupa jest równa:
Zadanie 25. (SP12)
Pole powierzchni jednej ściany sześcianu jest równe 4. Objętość tego sześcianu jest równa:
Zadanie 26. (SP12)
Tworząca stożka ma długość 4 i jest nachylona do płaszczyzny podstawy pod kątem 45 stopni .Wysokość tego stożka jest równa:
Zadanie 27. (SP12)
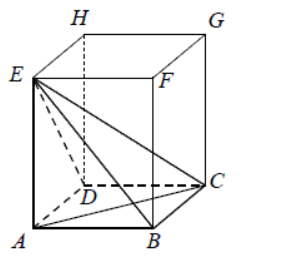
W graniastosłupie prawidłowym czworokątnym ABCDEFGH przekątna AC podstawy ma długość 4. Kąt ACE jest równy 60 stopni Oblicz objętość ostrosłupa ABCDE przedstawionego na poniższym rysunku.
Zadanie 28. (SP11)
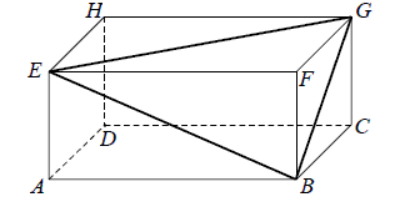
W prostopadłościanie ABCDEFGH mamy: |AB|=5,|AD|=4,|AE|=3. Który z odcinków AB,BG,GE,EB jest najdłuższy?
Zadanie 29. (SP11)
Pole powierzchni całkowitej sześcianu jest równe 54. Długość przekątnej tego sześcianu jest równa:
Zadanie 30. (SP11)
Objętość stożka o wysokości 8 i średnicy podstawy 12 jest równa:
Zadanie 31. (SP11)
Punkty K, L i M są środkami krawędzi BC, GH i AE sześcianu ABCDEFGH o krawędzi długości 1 (zobacz rysunek). Oblicz pole trójkąta KLM.
Zadanie 32. (SP10)
Pole powierzchni całkowitej prostopadłościanu o wymiarach 5×3×4 jest równe:
Zadanie 33. (SP10)
Ostrosłup ma 18 wierzchołków. Liczba wszystkich krawędzi tego ostrosłupa jest równa:
Zadanie 34. (SP10)
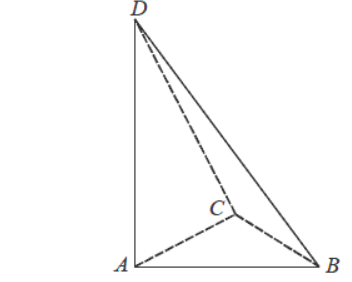
Podstawą ostrosłupa ABCD jest trójkąt ABC. Krawędź AD jest wysokością ostrosłupa (zobacz rysunek).
Oblicz objętość ostrosłupa ABCD, jeśli wiadomo, że AD=12, BC=6, BD=CD=13.
Zadanie 35. (SP09)
Powierzchnia boczna walca po rozwinięciu na płaszczyznę jest prostokątem. Przekątna tego prostokąta ma długość 12 i tworzy z bokiem, którego długość jest równa wysokości walca, kąt o mierze 30 stopni .
a) Oblicz pole powierzchni bocznej tego walca.
b) Sprawdź, czy objętość tego walca jest większa od . Odpowiedź uzasadnij.
a)
b)
Zadanie 36. (SP08)
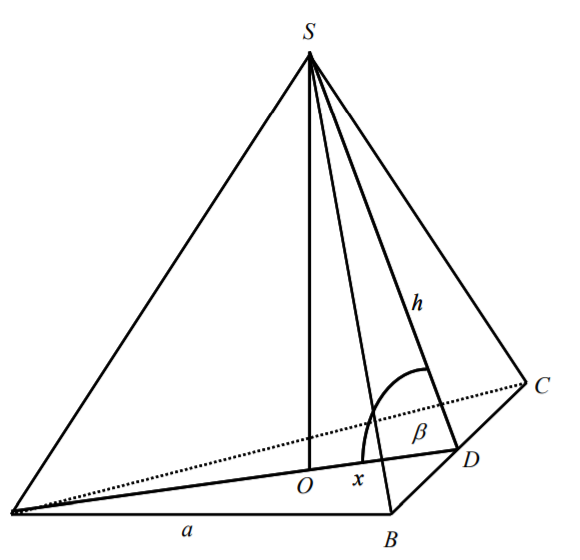
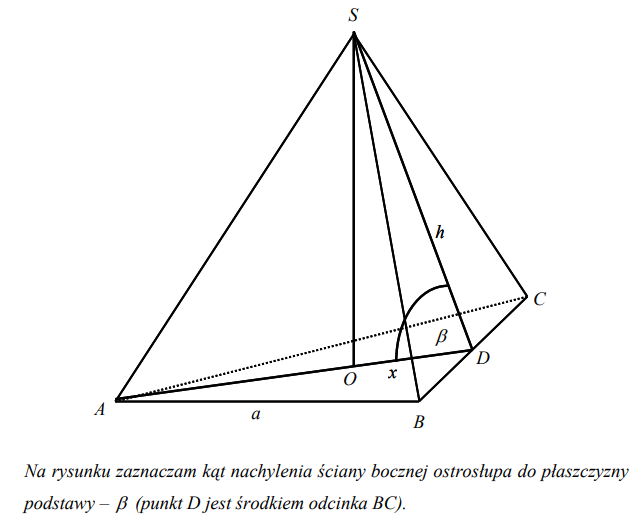
Pole powierzchni bocznej ostrosłupa prawidłowego trójkątnego równa się , gdzie a oznacza długość krawędzi podstawy tego ostrosłupa. Zaznacz na poniższym rysunku kąt nachylenia ściany bocznej ostrosłupa do płaszczyzny jego podstawy. Miarę tego kąta oznacz symbolem β . Oblicz cos β i korzystając z tablic funkcji trygonometrycznych i odczytaj przybliżoną wartość β z dokładnością do 1 stopnia.
Zadanie 38. (SP06)
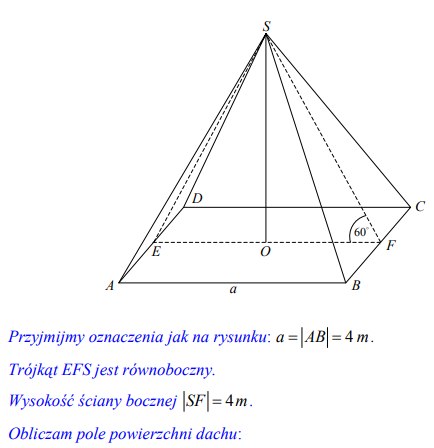
Dach wieży ma kształt powierzchni bocznej ostrosłupa prawidłowego czworokątnego, którego krawędź podstawy ma długość 4 m. Ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem 60 stopni .
a) Sporządź pomocniczy rysunek i zaznacz na nim podane w zadaniu wielkości.
b) Oblicz, ile sztuk dachówek należy kupić, aby pokryć ten dach, wiedząc, że do pokrycia 1 m2 potrzebne są 24 dachówki. Przy zakupie należy doliczyć 8% dachówek na zapas.
Zadanie 37. (SP07)
Dany jest graniastosłup czworokątny prosty ABCDEF GH o podstawach ABCD i EF GH oraz krawędziach bocznych AE , BF , CG , DH . Podstawa ABCD graniastosłupa jest rombem o boku długości 8 cm i kątach ostrych A i C o mierze 60 stopni. . Przekątna graniastosłupa CE jest nachylona do płaszczyzny podstawy pod kątem 60 stopni . Sporządź rysunek pomocniczy i zaznacz na nim wymienione w zadaniu kąty. Oblicz objętość tego graniastosłupa.
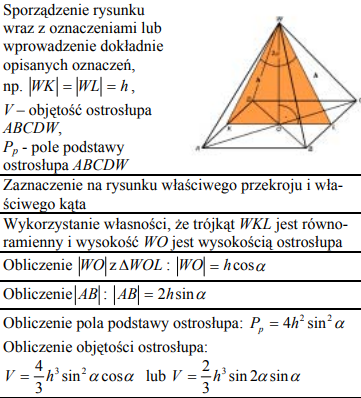
Zadanie 39. (SP05)
W ostrosłupie czworokątnym prawidłowym wysokości przeciwległych ścian bocznych poprowadzone z wierzchołka ostrosłupa mają długości h i tworzą kąt o mierze 2α. Oblicz objętość tego ostrosłupa.