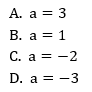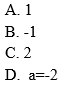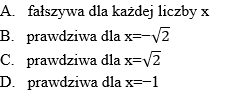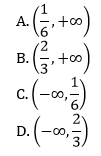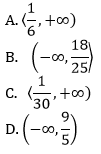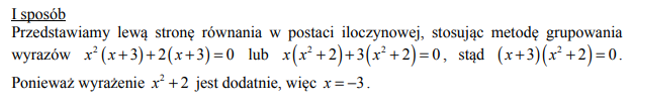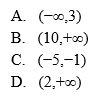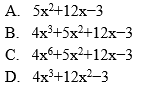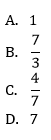Zadania maturalne z Matematyki
Tematyka: algebra: równania z niewiadomymi, wzory skróconego mnożenia.
Zadania pochodzą z oficjalnych arkuszy maturalnych CKE, które służyły przeprowadzaniu majowych egzaminów. Czteroznakowy kod zapisany przy każdym zadaniu wskazuje na jego pochodzenie: S/N – „stara”/”nowa” formuła; P/R – poziom podstawowy/rozszerzony; np. 08 – rok 2008.
Zbiór zadań maturalnych w formie arkuszy, możesz pobrać >> TUTAJ <<.
Zadanie 1. (NP15)
Układ równań opisuje w układzie współrzędnych na płaszczyźnie:
Zadanie 2. (NP15)
Suma wszystkich pierwiastków równania (x+3)(x+7)(x-11)=0 jest równa:
Zadanie 3. (NP15)
Równanie x−1x+1=x−1:
Zadanie 4. (NP16)
Równość jest prawdziwa dla:
Zadanie 5. (NP16)
Jedną z liczb, które spełniają nierówność −x5+x3−x<−2, jest:
Zadanie 6. (NP16)
Rozwiąż równanie
Zadanie 7. (NP16)
Równanie wymierne , gdzie x≠−5:
Zadanie 8. (NP17)
Równość jest:
Zadanie 9. (NP17)
Do zbioru rozwiązań nierówności (x4+1)(2−x)>0 nie należy liczba:
Zadanie 10. (NP17)
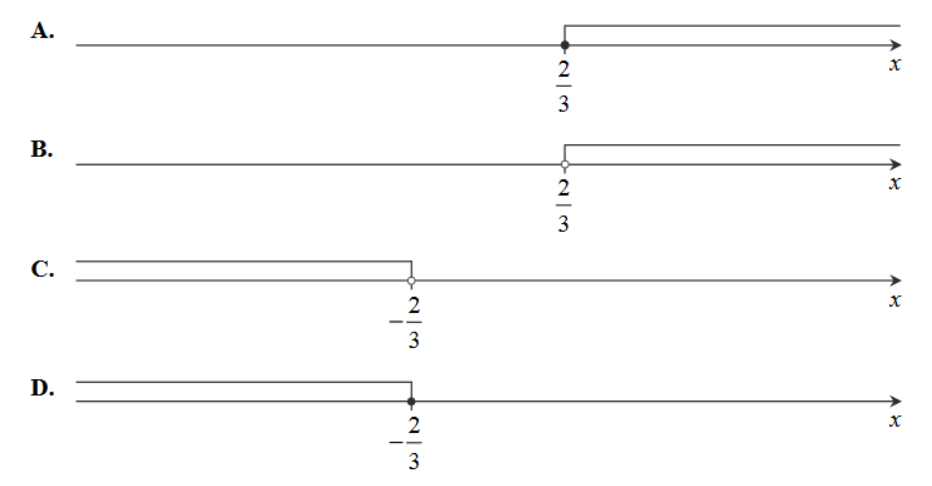
Wskaż rysunek, na którym jest przedstawiony zbiór wszystkich rozwiązań nierówności 2−3x≥4.
Zadanie 11. (NP17)
Równanie x(x2−4)(x2+4)=0 z niewiadomą x:
Zadanie 12. (NP18)
Zbiorem wszystkich rozwiązań nierówności jest przedział:
Zadanie 13. (NP18)
Rozwiąż równanie (x3+125)(x2−64)=0.
Zadanie 14. (SP15)
Zbiorem wszystkich rozwiązań nierówności jest przedział:
Zadanie 16. (SP16)
Rozwiąż równanie x3+3x2+2x+6=0.
Zadanie 17. (SP14)
Wspólnym pierwiastkiem równań (x2−1)(x−10)(x−5)=0 i jest liczba:
Zadanie 18. (SP14)
Rozwiąż równanie 9x3+18x2−4x−8=0.
Zadanie 19. (SP13)
Liczba rzeczywistych rozwiązań równania (x+1)(x+2)(x2+3)=0 jest równa:
Zadanie 20. (SP13)
Rozwiąż równanie x3+2x2−8x−16=0.
Zadanie 21. (SP12)
Liczby x1=−4 i x2=3 są pierwiastkami wielomianu W(x)=x3+4x2−9x−36. Oblicz trzeci pierwiastek tego wielomianu.
X3 = -3
Zadanie 22. (SP11)
Rozwiązanie równania x(x+3)−49=x(x−4) należy do przedziału:
Zadanie 23. (SP11)
Zbiorem wszystkich rozwiązań nierówności jest przedział:
Zadanie 24. (SP10)
Dane są wielomiany W(x)=−2x3+5x2−3 oraz P(x)=2x3+12x. Wielomian W(x)+P(x) jest równy:
Zadanie 25. (SP10)
Rozwiązaniem równania jest:
Zadanie 26. (SP10)
Rozwiąż równanie x3−7x2−4x+28=0.
Zadanie 27. (SP09)
Wielomian W dany jest wzorem W (x) = x3 + ax2 − 4x + b
a) Wyznacz a,b oraz c tak, aby wielomian W był równy wielomianowi P , gdy:
P (x) = x3 + (2a + 3)x 2 + (a + b + c)x − 1 .
b) Dla a = 3 i b = 0 zapisz wielomian W w postaci iloczynu trzech wielomianów stopnia pierwszego.
Zadanie 28. (SP08)
Dany jest wielomian W (x) = x3 − 5x2 − 9x + 45.
a) Sprawdź, czy punkt A = (1,30) należy do wykresu tego wielomianu.
b) Zapisz wielomian W w postaci iloczynu trzech wielomianów stopnia pierwszego.
Zadanie 29. (SP07)
Dany jest wielomian W (x) = 2x3 + ax2 − 14x + b .
a) Dla a = 0 i b = 0 otrzymamy wielomian W (x) = 2x 3 − 14x . Rozwiąż równanie 2x3 − 14x = 0 .
b) Dobierz wartości a i b tak, aby wielomian W (x) był podzielny jednocześnie przez x− 2 oraz x+ 3 .
Zadanie 30. (SP06)
Liczby 3 i –1 są pierwiastkami wielomianu W(x)=2x3+ax2+bx+30
a) Wyznacz wartości współczynników a i b.
b) Oblicz trzeci pierwiastek tego wielomianu.
Zadanie 31. (SP05)
Dany jest wielomian W(x)=x3+kx2-4
a) Wyznacz współczynnik k tego wielomianu wiedząc, że wielomian ten jest podzielny przez dwumian x + 2
b) Dla wyznaczonej wartości k rozłóż wielomian na czynniki i podaj wszystkie jego pierwiastki.