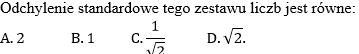Zadania maturalne z Matematyki

Tematyka: statystyka opisowa: mediana, moda, średnia arytmetyczna, odchylenie standardowe, wariancja.

Zadania pochodzą z oficjalnych arkuszy maturalnych CKE, które służyły przeprowadzaniu majowych egzaminów. Czteroznakowy kod zapisany przy każdym zadaniu wskazuje na jego pochodzenie: S/N – „stara”/”nowa” formuła; P/R – poziom podstawowy/rozszerzony; np. 08 – rok 2008.

Zbiór zadań maturalnych w formie arkuszy, możesz pobrać >> TUTAJ <<.

Zadanie 1. (NP15)
Średnia arytmetyczna zestawu danych:

2,4,7,8,9

jest taka sama jak średnia arytmetyczna zestawu danych:

2,4,7,8,9,x.

Wynika stąd, że

Zadanie 2. (NP16)
Średnia arytmetyczna sześciu liczb naturalnych: 31,16,25,29,27,x, jest równa . Mediana tych liczb jest równa:

Zadanie 3. (NP16)
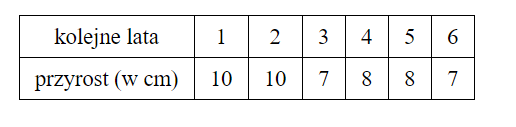
W tabeli przedstawiono roczne przyrosty wysokości pewnej sosny w ciągu sześciu kolejnych lat.

Oblicz średni roczny przyrost wysokości tej sosny w badanym okresie sześciu lat. Otrzymany wynik zaokrąglij do 1 cm. Oblicz błąd względny otrzymanego przybliżenia. Podaj ten błąd w procentach.

Zadanie 4. (NP17)
Średnia arytmetyczna ośmiu liczb: 3,5,7,9,x,15,17,19 jest równa 11. Wtedy:

Zadanie 5. (NP18)
W zestawie 2,2,2,…,2 ( m liczb),4,4,4,…, ( m liczb) jest 2m liczb (m≥1), w tym m liczb 2 i m liczb 4.

Odchylenie standardowe tego zestawu liczb jest równe:

Zadanie 6. (SP14)
Mediana zestawu danych 2,12,a,10,5,3 jest równa 7. Wówczas:

Zadanie 7. (SP14)
Mediana uporządkowanego niemalejąco zestawu sześciu liczb: 1,2,3,x,5,8 jest równa 4. Wtedy:

 Zadanie 8. (SP12)
Średnia arytmetyczna cen sześciu akcji na giełdzie jest równa 500 zł. Za pięć z tych akcji zapłacono 2300 zł. Cena szóstej akcji jest równa:

Zadanie 9. (SP11)
Uczniowie pewnej klasy zostali poproszeni o odpowiedź na pytanie: „Ile osób liczy twoja rodzina?” Wyniki przedstawiono w tabeli:

Średnia liczba osób w rodzinie dla uczniów tej klasy jest równa 4. Wtedy liczba x jest równa:

Zadanie 10. (SP10)
Średnia arytmetyczna dziesięciu liczb x,3,1,4,1,5,1,4,1,5 jest równa 3. Wtedy:

Zadanie 11. (SP09)
Tabela przedstawia wyniki części teoretycznej egzaminu na prawo jazdy. Zdający uzyskał wynik pozytywny, jeżeli popełnił co najwyżej dwa błędy.

a) Oblicz średnią arytmetyczną liczby błędów popełnionych przez zdających ten egzamin. Wynik podaj w zaokrągleniu do całości
b) Oblicz prawdopodobieństwo, że wśród dwóch losowo wybranych zdających tylko jeden uzyskał wynik pozytywny. Wynik zapisz w postaci ułamka zwykłego nieskracalnego.

Zadanie 12. (SP06)
Kostka masła produkowanego przez pewien zakład mleczarski ma nominalna masę 20 dag. W czasie kontroli zakładu zważono 150 losowo wybranych kostek masła.
Wyniki badan przedstawiono w tabeli.

a) Na podstawie danych przedstawionych w tabeli oblicz średnia arytmetyczna oraz odchylenie standardowe masy kostki masła.
b) Kontrola wypada pozytywnie jeśli średnia masa koski masła jest równa masie nominalnej i odchylenie standardowe nie przekracza 1 dag. Czy kontrola zakładu wypadła pozytywnie? Odpowiedz uzasadnij.

Zadanie 13. (SP05)
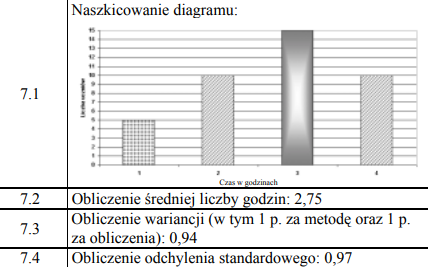
W poniższej tabeli przedstawiono wyniki sondażu przeprowadzonego w grupie uczniów, dotyczącego czasu przeznaczanego dziennie na przygotowanie zadań domowych.

a) Naszkicuj diagram słupkowy ilustrujący wyniki tego sondażu.
b) Oblicz średnią liczbę godzin, jaką uczniowie przeznaczają dziennie na przygotowanie zadań domowych.
c) Oblicz wariancję i odchylenie standardowe czasu przeznaczonego dziennie na przygotowanie zadań domowych. Wynik podaj z dokładnością do 0,01.