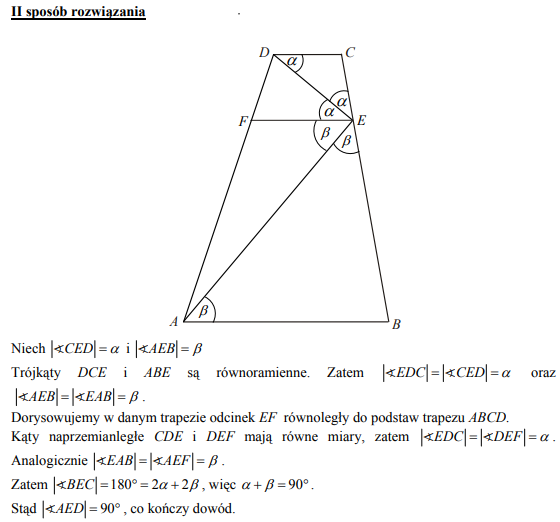
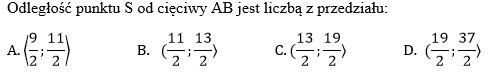Zadania maturalne z Matematyki
Tematyka: planimetria (geometria płaska), własności: czworokątów, trójkątów, okręgu i koła.
Zadania pochodzą z oficjalnych arkuszy maturalnych CKE, które służyły przeprowadzaniu majowych egzaminów. Czteroznakowy kod zapisany przy każdym zadaniu wskazuje na jego pochodzenie: S/N – „stara”/”nowa” formuła; P/R – poziom podstawowy/rozszerzony; np. 08 – rok 2008.
Zbiór zadań maturalnych w formie arkuszy, możesz pobrać >> TUTAJ <<.
Zadanie 1. (NP15)
Pole rombu o obwodzie 8 jest równe 1. Kąt ostry tego rombu ma miarę α. Wtedy:
Zadanie 2. (NP15)
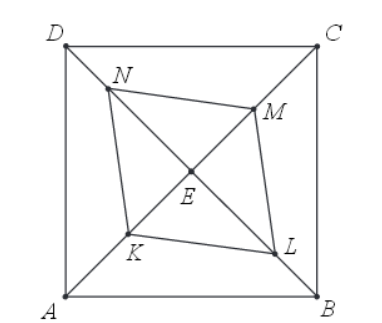
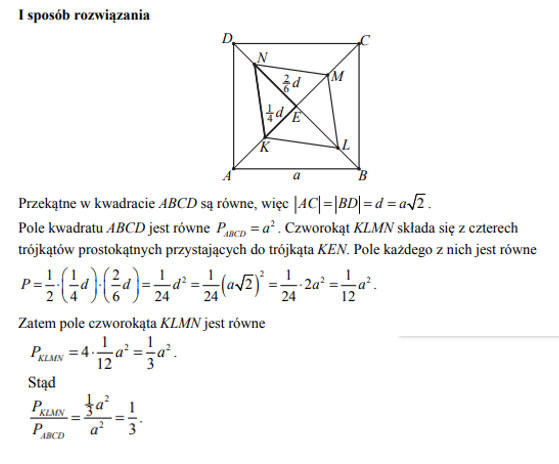
Dany jest kwadrat ABCD. Przekątne AC i BD przecinają się w punkcie E. Punkty K i M są środkami odcinków – odpowiednio AE i EC. Punkty L i N leżą na przekątnej BD tak, że |BL|= |BE| i |DN|=
|DE| (zobacz rysunek). Wykaż, że stosunek pola czworokąta KLMN do pola kwadratu ABCD jest równy 1:3.
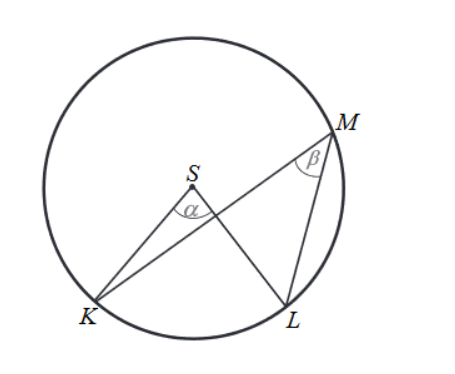
Zadanie 3. (NP16)
Punkty ABCD leżą na okręgu o środku S (zobacz rysunek). Miara kąta BDC jest równa:
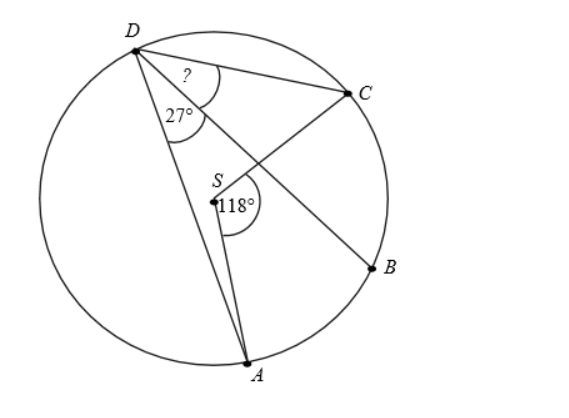
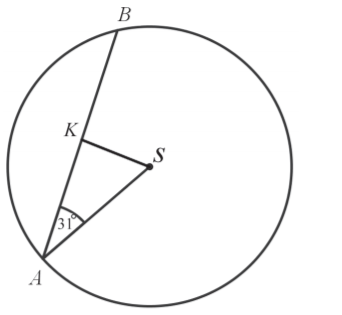
Zadanie 4. (NP16)
W okręgu o środku w punkcie S poprowadzono cięciwę AB, która utworzyła z promieniem AS kąt o mierze 31st. (zobacz rysunek). Promień tego okręgu ma długość 10.
Zadanie 5. (NP16)
Przedstawione na rysunku trójkąty ABC i PQR są podobne. Bok AB trójkąta ABC ma długość:
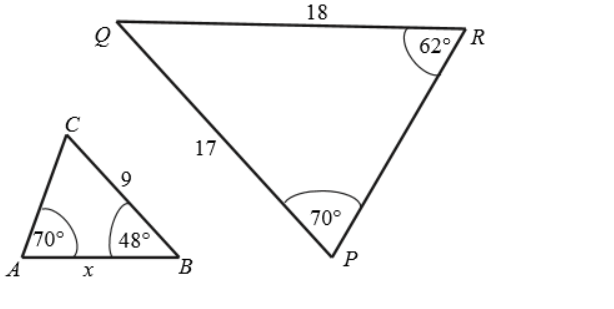
8,5*
Zadanie 5. (NP16)
Z odcinków o długościach: 5,2a+1,a−1 można zbudować trójkąt równoramienny. Wynika stąd, że:
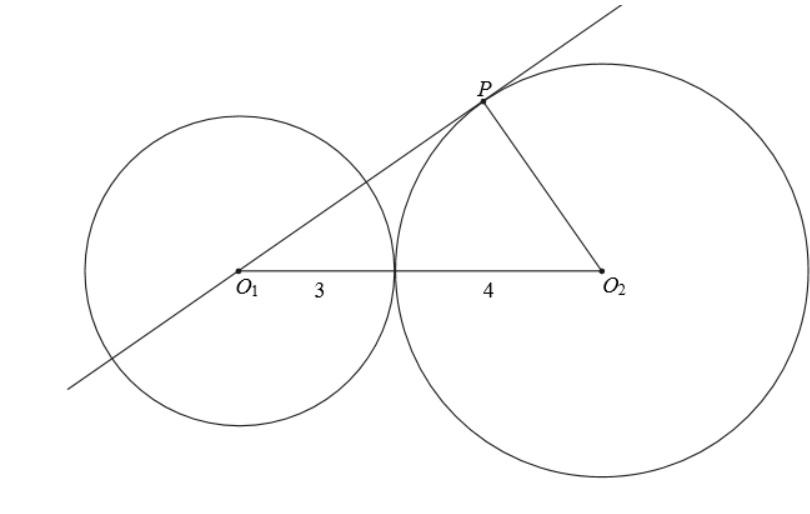
Zadanie 6. (NP16)
Okręgi o promieniach 3 i 4 są styczne zewnętrznie. Prosta styczna do okręgu o promieniu 4 w punkcie P przechodzi przez środek okręgu o promieniu 3 (zobacz rysunek).
Zadanie 7. (NP16)
Dany jest trójkąt prostokątny ABC. Na przyprostokątnych AC i AB tego trójkąta obrano odpowiednio punkty D i G. Na przeciwprostokątnej BC wyznaczono punkty E i F takie, że |∢DEC|=|∢BGF|=90st. (zobacz rysunek). Wykaż, że trójkąt CDE jest podobny do trójkąta FBG.
Zadanie 8. (NP16)
Jeden z kątów trójkąta jest trzy razy większy od mniejszego z dwóch pozostałych kątów, które różnią się o 50st. .Oblicz kąty tego trójkąta.
Zadanie 9. (NP17)
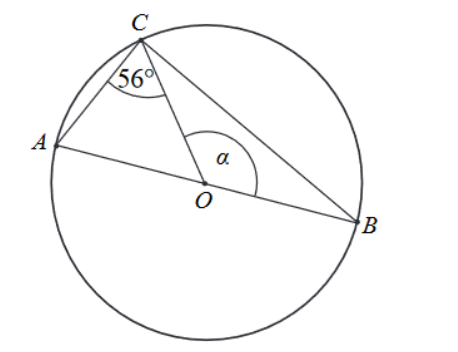
Na okręgu o środku w punkcie O leży punkt C (zobacz rysunek). Odcinek AB jest średnicą tego okręgu. Zaznaczony na rysunku kąt środkowy α ma miarę:
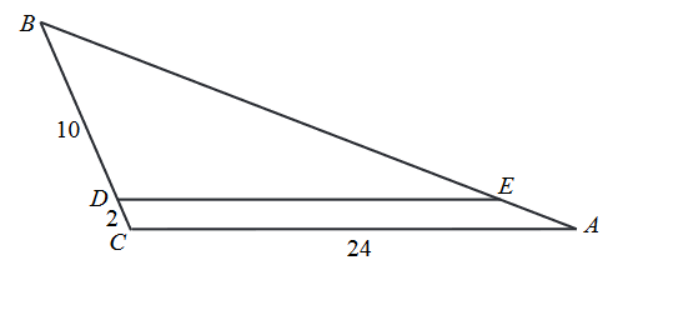
Zadanie 10. (NP17)
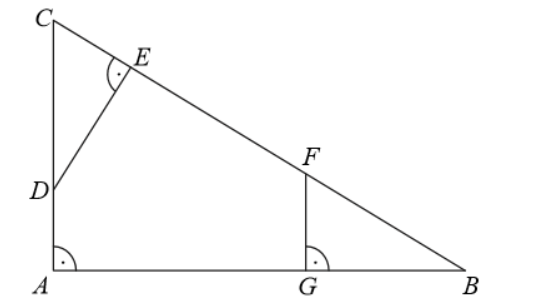
W trójkącie ABC punkt D leży na boku BC, a punkt E leży na boku AB. Odcinek DE jest równoległy do boku AC, a ponadto |BD|=10, |BC|=12 i |AC|=24 (zobacz rysunek).
Zadanie 11. (NP17)
Obwód trójkąta przedstawionego na rysunku jest równy:
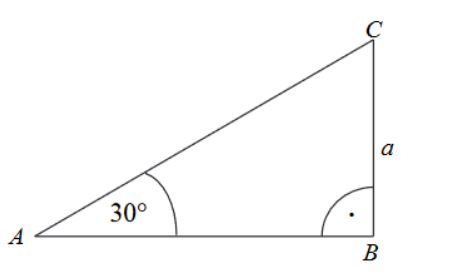
Zadanie 12. (NP17)
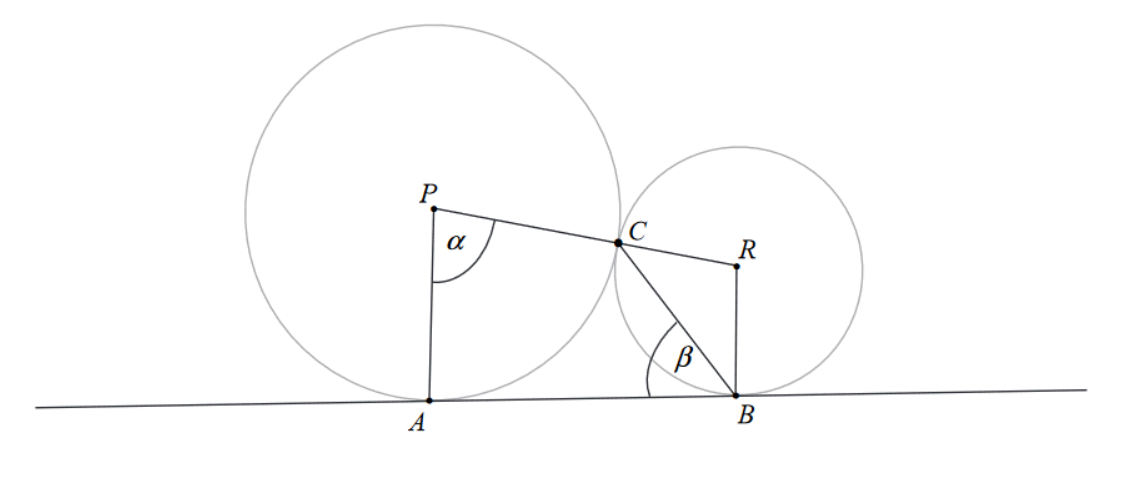
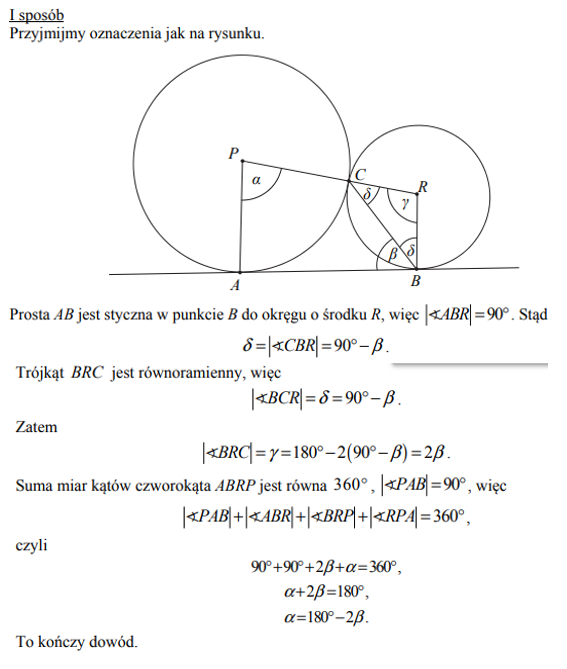
Dane są dwa okręgi o środkach w punktach P i R, styczne zewnętrznie w punkcie C. Prosta AB jest styczna do obu okręgów odpowiednio w punktach A i B oraz |∢APC|=α i |∢ABC|=β (zobacz rysunek). Wykaż, że α=180st−2β.
Zadanie 13. (NP17)
Przeciwprostokątna trójkąta prostokątnego ma długość 26 cm, a jedna z przyprostokątnych jest o 14 cm dłuższa od drugiej. Oblicz obwód tego trójkąta.
Zadanie 14. (NP18)
Dany jest trójkąt o bokach długości: Trójkątem podobnym do tego trójkąta jest trójkąt, którego boki mają długości:
Zadanie 16. (NP18)
Dany jest trapez prostokątny KLMN, którego podstawy mają długości |KL|=a, |MN|=b, a>b. Kąt KLM ma miarę 60st .Długość ramienia LM tego trapezu jest równa:
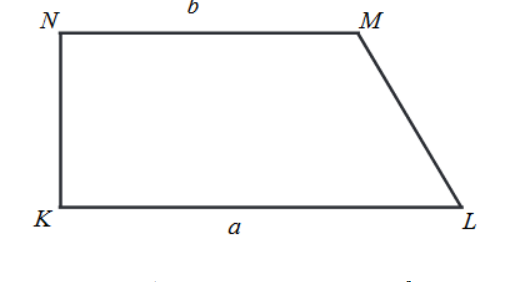
Zadanie 17. (NP18)
Okręgi o środkach odpowiednio A i B są styczne zewnętrznie i każdy z nich jest styczny do obu ramion danego kąta prostego (zobacz rysunek). Promień okręgu o środku A jest równy 2.
Uzasadnij, że promień okręgu o środku B jest mniejszy od
Zadanie 18. (SP15)
W trójkącie równoramiennym ABC spełnione są warunki: |AC|=|BC|, |∢CAB|=50st. Odcinek BD jest dwusieczną kąta ABC, a odcinek BE jest wysokością opuszczoną z wierzchołka B na bok AC. Miara kąta EBD jest równa:
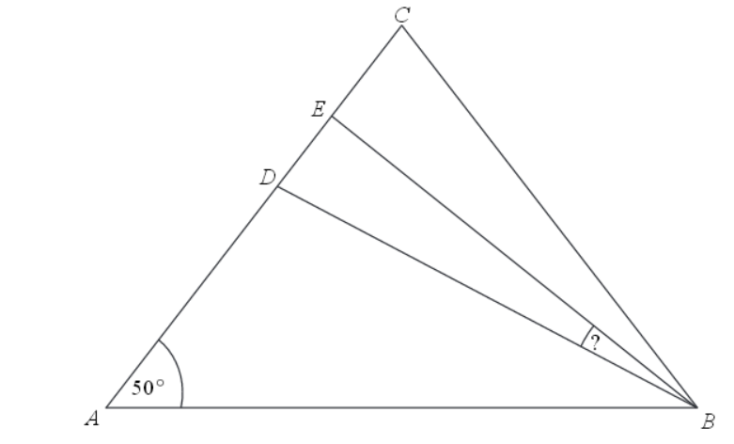
Zadanie 19. (SP15)
Przedstawione na rysunku trójkąty są podobne.
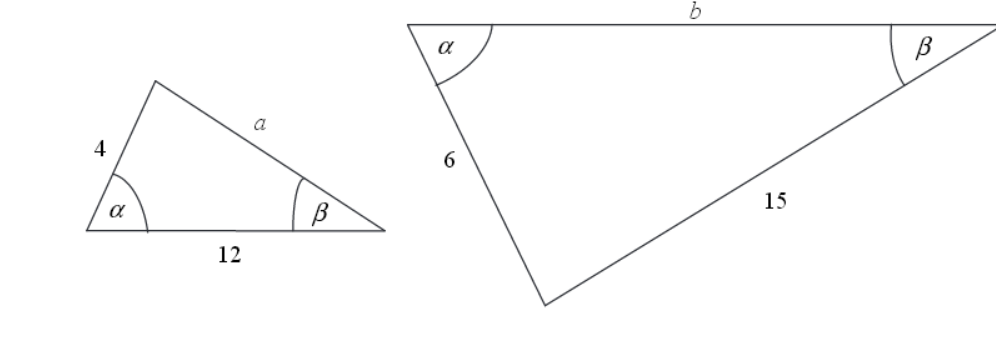
Zadanie 20. (SP15)
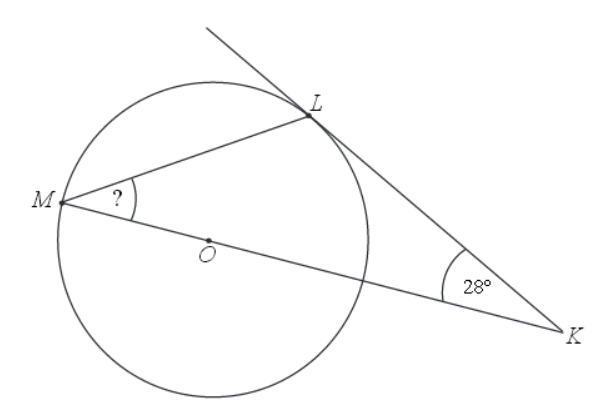
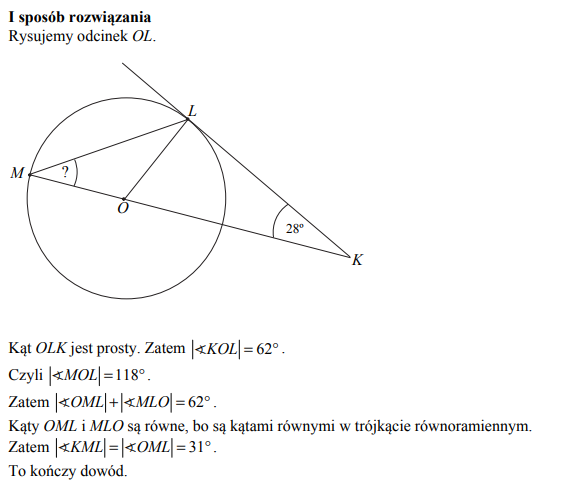
Dany jest okrąg o środku w punkcie O. Prosta KL jest styczna do tego okręgu w punkcie L, a środek O tego okręgu leży na odcinku KM (zobacz rysunek). Udowodnij, że kąt KML ma miarę 31st.
Zadanie 21. (SP16)
Dany jest trójkąt prostokątny ABC. Na przyprostokątnych AC i AB tego trójkąta obrano odpowiednio punkty D i G. Na przeciwprostokątnej BC wyznaczono punkty E i F takie, że |∢DEC|=|∢BGF|=90st. (zobacz rysunek). Wykaż, że trójkąt CDE jest podobny do trójkąta FBG.
Zadanie 22. (SP16)
Jeden z kątów trójkąta jest trzy razy większy od mniejszego z dwóch pozostałych kątów, które różnią się o 50st. Oblicz kąty tego trójkąta.
Zadanie 23. (SP14)
Jeżeli trójkąty ABC i A′B′C′ są podobne, a ich pola są, odpowiednio, równe 25 cm2 i 50 cm2, to skala podobieństwa jest równa:
Zadanie 24. (SP14)
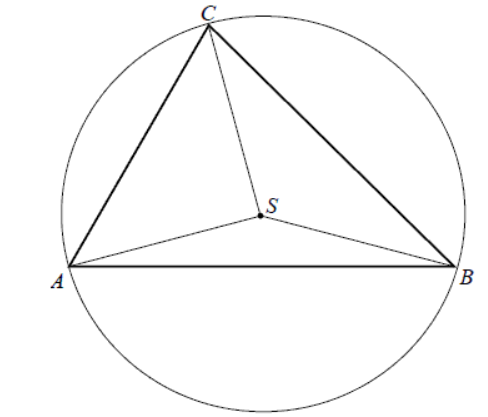
Środek S okręgu opisanego na trójkącie równoramiennym ABC, o ramionach AC i BC, leży wewnątrz tego trójkąta.
Wykaż, że miara kąta wypukłego ASB jest cztery razy większa od miary kąta wypukłego SBC.
Zadanie 25. (SP14)
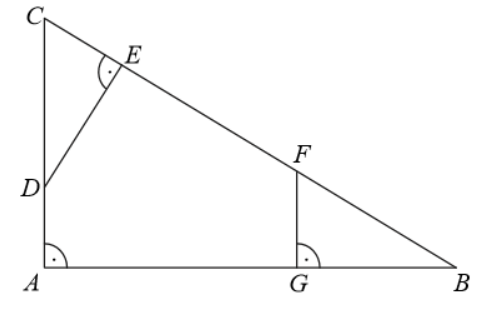
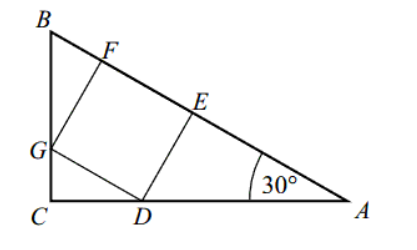
Kąt CAB trójkąta prostokątnego ACB ma miarę 30st .
Pole kwadratu DEFG, wpisanego w ten trójkąt (zobacz rysunek), jest równe 4. Oblicz pole trójkąta ACB.
Zadanie 26. (SP13)
Średnice AB i CD okręgu o środku S przecinają się pod kątem 50st (tak jak na rysunku).
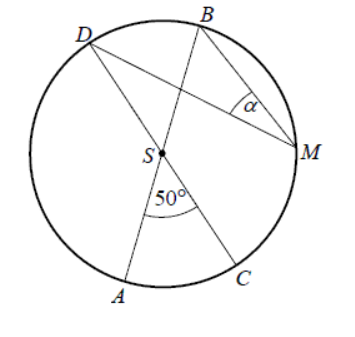
Zadanie 27. (SP13)
Punkt S jest środkiem okręgu opisanego na trójkącie ostrokątnym ABC. Kąt ACS jest trzy razy większy od kąta BAS, a kąt CBS jest dwa razy większy od kąta BAS. Oblicz kąty trójkąta ABC.
Zadanie 28. (SP12)
W trójkącie równoramiennym ABC dane są |AC|=|BC|=5 oraz wysokość |CD|=2. Podstawa AB tego trójkąta ma długość:
Zadanie 29. (SP12)
W trójkącie prostokątnym dwa dłuższe boki mają długości 5 i 7. Obwód tego trójkąta jest równy:
Zadanie 30. (SP12)
Odcinki AB i CD są równoległe i |AB|=5,|AC|=2,|CD|=7 (zobacz rysunek). Długość odcinka AE jest równa:
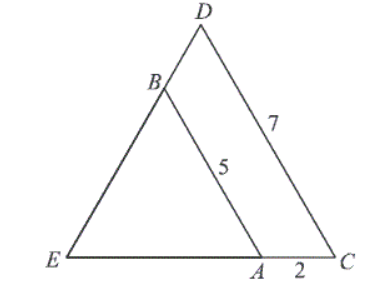
Zadanie 31. (SP12)
Pole kwadratu wpisanego w okrąg o promieniu 5 jest równe:
Zadanie 32. (SP12)
Punkty A,B,C,D dzielą okrąg na 4 równe łuki. Miara zaznaczonego na rysunku kąta wpisanego ACD jest równa
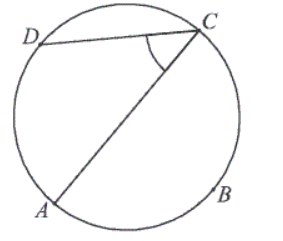
Zadanie 33. (SP12)
Miary kątów czworokąta tworzą ciąg arytmetyczny o różnicy 20st. Najmniejszy kąt tego czworokąta ma miarę:
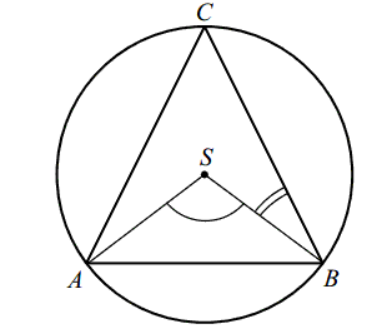
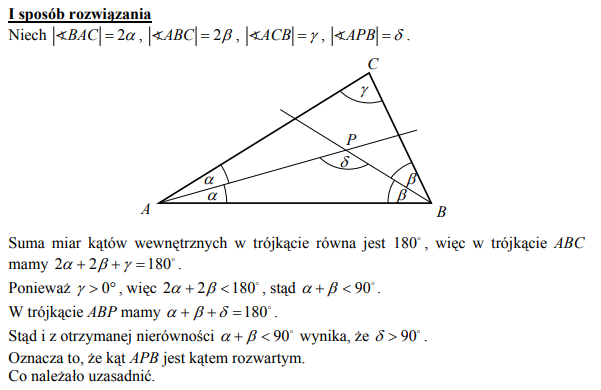
Zadanie 34. (SP12)
W trójkącie ABC poprowadzono dwusieczne kątów A i B. Dwusieczne te przecinają się w punkcie P. Uzasadnij, że kąt APB jest rozwarty.
Zadanie 35. (SP11)
Punkt O jest środkiem okręgu. Kąt wpisany α ma miarę:
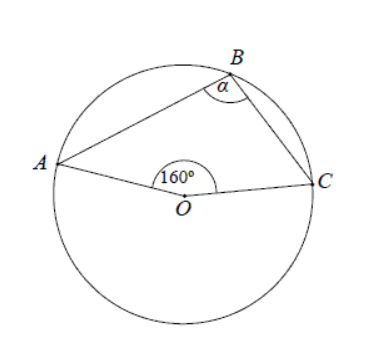
Zadanie 36. (SP11)
Wysokość rombu o boku długości 6 i kącie ostrym 60st jest równa:
Zadanie 37. (SP11)
Dany jest czworokąt ABCD, w którym AB∥CD. Na boku BC wybrano taki punkt E, że |EC|=|CD| i |EB|=|BA|. Wykaż, że kąt AED jest prosty.
Zadanie 38. (SP10)
Liczba przekątnych siedmiokąta foremnego jest równa:
Zadanie 39. (SP10)
Okrąg opisany na kwadracie ma promień 4. Długość boku tego kwadratu jest równa:
Zadanie 40. (SP10)
Podstawa trójkąta równoramiennego ma długość 6, a ramię ma długość 5. Wysokość opuszczona na podstawę ma długość:
Zadanie 41. (SP10)
Odcinki AB i DE są równoległe. Długości odcinków CD,DE i AB są odpowiednio równe 1, 3 i 9. Długość odcinka AD jest równa:
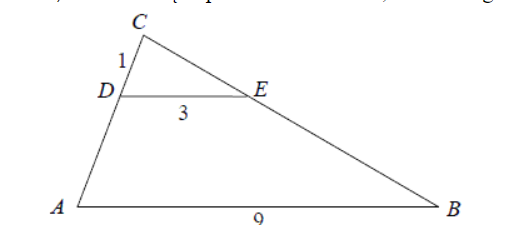
Zadanie 42. (SP10)
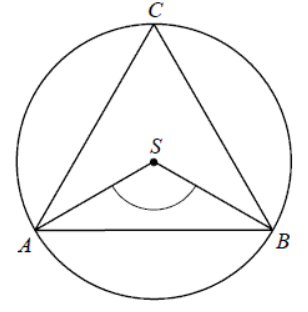
Punkty A,B,C leżące na okręgu o środku S są wierzchołkami trójkąta równobocznego.
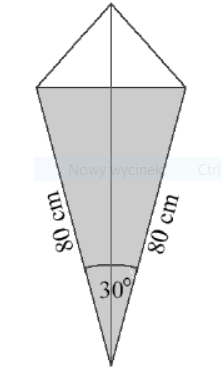
Zadanie 43. (SP10)
Latawiec ma wymiary podane na rysunku.
Zadanie 44. (SP10)
Trójkąty prostokątne równoramienne ABC i CDE są położone tak, jak na poniższym rysunku (w obu trójkątach kąt przy wierzchołku C jest prosty). Wykaż, że AD=BE.
Zadanie 45. (SP10)
W trapezie prostokątnym krótsza przekątna dzieli go na trójkąt prostokątny i trójkąt równoboczny. Dłuższa podstawa trapezu jest równa 6. Oblicz obwód tego trapezu.
Wynik to 15 + 3√3
Zadanie 46. (SP09)
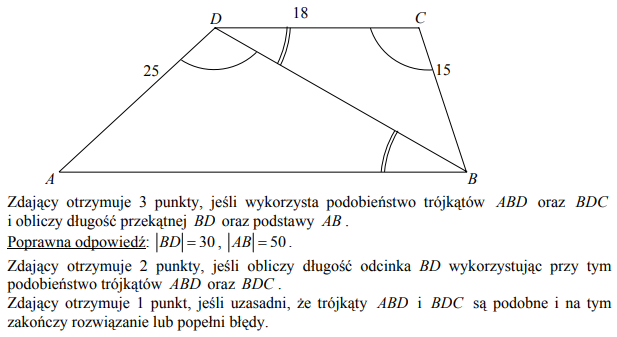
W trapezie ABCD długość podstawy CD jest równa 18 , a długości ramion trapezu AD i BC są odpowiednio równe 25 i 15. Kąty ADB i DCB, zaznaczone na rysunku, mają równe miary. Oblicz obwód tego trapezu.
Zadanie 47. (SP08)
Liczba przekątnych wielokąta wypukłego, w którym jest n boków i n ≥ 3 wyraża się wzorem Pn = .
a) Oblicz liczbę przekątnych w dwudziestokącie wypukłym.|
b) Oblicz, ile boków ma wielokąt wypukły, w którym liczba przekątnych jest pięć razy większa od liczby boków.
c) Sprawdź, czy jest prawdziwe następujące stwierdzenie: Każdy wielokąt wypukły o parzystej liczbie boków ma parzystą liczbę przekątnych. Odpowiedź uzasadnij.
d) Uzasadnij, że jeżeli liczba boków wielokąta wypukłego jest nieparzysta, to liczba jego przekątnych jest wielokrotnością liczby jego boków.
Zadanie 48. (SP08)
Dany jest trapez, w którym podstawy mają długość 4 cm i 10 cm oraz ramiona tworzą z dłuższą podstawą kąty o miarach 30st i 45st . Oblicz wysokość tego trapezu.
Zadanie 49. (SP07)
Oblicz pole czworokąta wypukłego ABCD , w którym kąty wewnętrzne mają odpowiednio miary: ∡A =90st , ∡B =75st , ∡C =60st , ∡D =135st , a boki AB i AD mają długość 3 cm. Sporządź rysunek pomocniczy.
Zadanie 50. (SP06)
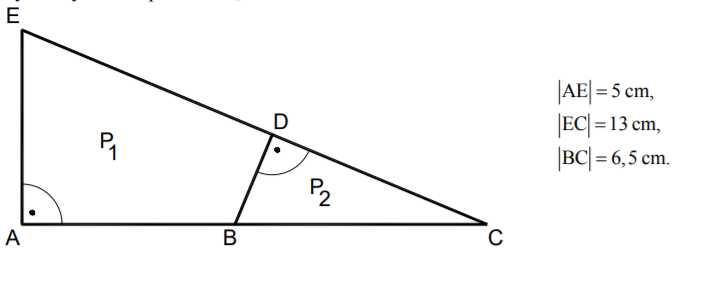
Państwo Nowakowie przeznaczyli 26000 zł na zakup działki. Do jednej z ofert dołączono rysunek dwóch przylegających do siebie działek w skali 1:1000. Jeden metr kwadratowy gruntu w tej ofercie kosztuje 35 zł. Oblicz, czy przeznaczona przez państwa Nowaków kwota wystarczy na zakup działki P2.
Zadanie 51. (SP06)
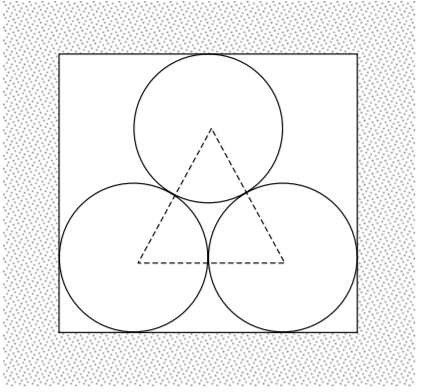
Szkic przedstawia kanał ciepłowniczy, którego przekrój poprzeczny jest prostokątem. Wewnątrz kanału znajduje się rurociąg składający się z trzech rur, każda o średnicy zewnętrznej 1 m. Oblicz wysokość i szerokość kanału ciepłowniczego. Wysokość zaokrąglij do 0,01 m.
Zadanie 52. (SP05)
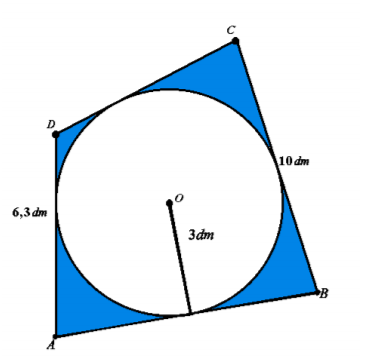
Z kawałka materiału o kształcie i wymiarach czworokąta ABCD (patrz na rysunek poniżej) wycięto okrągłą serwetkę o promieniu 3 dm. Oblicz, ile procent całego materiału stanowi jego niewykorzystana część. Wynik podaj z dokładnością do 0,01 procenta.