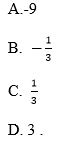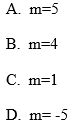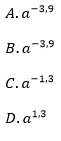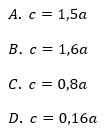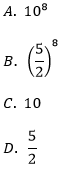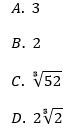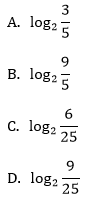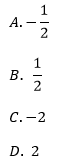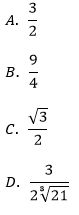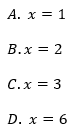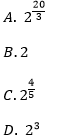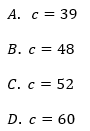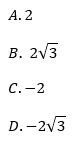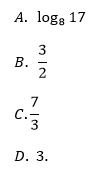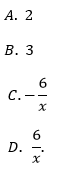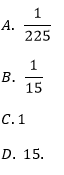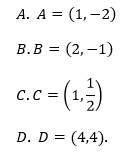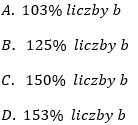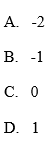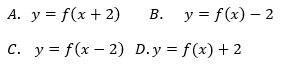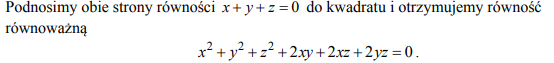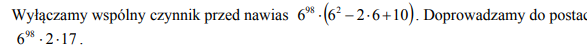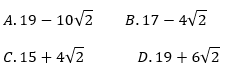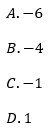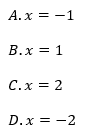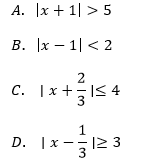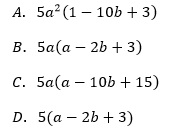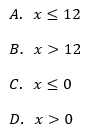Zadania maturalne z Matematyki

Tematyka: właściwości liczb, zbiory liczbowe, pierwiastki, potęgi, logarytmy, ułamki, procenty.

Zadania pochodzą z oficjalnych arkuszy maturalnych CKE, które służyły przeprowadzaniu majowych egzaminów. Czteroznakowy kod zapisany przy każdym zadaniu wskazuje na jego pochodzenie: S/N – „stara”/”nowa” formuła; P/R – poziom podstawowy/rozszerzony; np. 08 – rok 2008.

Zbiór zadań maturalnych w formie arkuszy, możesz pobrać >> TUTAJ <<.

Zadanie 1. (NP15)
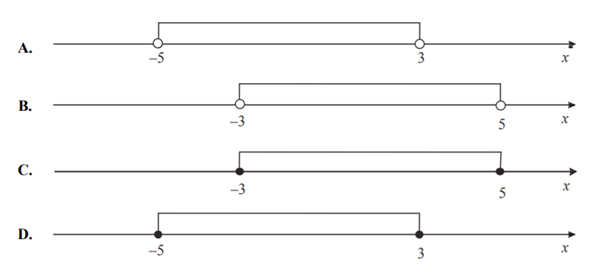
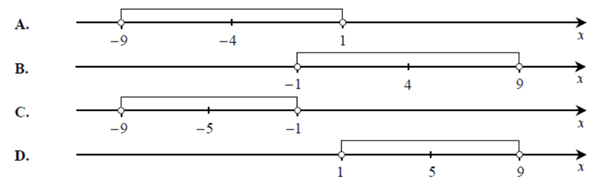
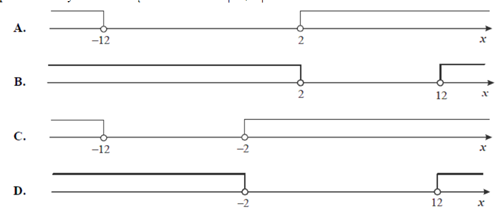
Wskaż rysunek, na którym przedstawiono przedział, będący zbiorem wszystkich rozwiązań nierówności − 4 ≤ x − 1 ≤ 4 .

Zadanie 2. (NP15)
Dane są liczby .
Iloczyn abc jest równy:

Zadanie 3. ((NP15)
Kwotę 1000 zł ulokowano w banku na roczną lokatę oprocentowaną w wysokości 4% w stosunku rocznym. Po zakończeniu lokaty od naliczonych odsetek odprowadzany jest podatek w wysokości 19%. Maksymalna kwota, jaką po upływie roku będzie można wypłacić z banku, jest równa:

Zadanie 4. (NP15)
Równość zachodzi dla:

Zadanie 5. (NP15)
Ile liczb całkowitych x spełnia nierówność

Zadanie 6. (NP15)
Wykaż, że dla każdej liczby rzeczywistej x i dla każdej liczby rzeczywistej y prawdziwa jest nierówność

Zadanie 7. (NP15)
Jeżeli do licznika i do mianownik nieskracalnego dodatniego ułamka dodamy połowę jego licznika, to otrzymamy , a jeżeli do licznika i do mianownika dodamy 1, to otrzymamy  . Wyznacz ten ułamek.

Zadanie 8. (NP15)
Dla każdej dodatniej liczby a iloraz  jest równy

Zadanie 9. (NP15)
Liczba  jest równa

Zadanie 10. (NP15)
Liczby a i c są dodatnie. Liczba b stanowi 48% liczby a oraz 32% liczby c. Wynika stąd, że

Zadanie 11. (NP16)
Skala Richtera służy do określania siły trzęsień ziemi. Siła ta opisana jest wzorem R= , gdzie A oznacza amplitudę trzęsienia wyrażoną w centymetrach, A₀=10⁻⁴ cm jest stałą, nazywaną amplitudą wzorcową. 5 maja 2014 roku w Tajlandii miało miejsce trzęsienie ziemi o sile 6,2 w skali Richtera. Oblicz amplitudę trzęsienia ziemi w Tajlandii i rozstrzygnij, czy jest ona większa, czy – mniejsza od 100 cm.

Zadanie 12. (NP17)
Liczba jest równa:

Zadanie 13. (NP17)
Liczba    jest równa:

Zadanie 14. (NP17)
Liczba  jest równa

Zadanie 15. (NP17)
Liczba osobników pewnego zagrożonego wyginięciem gatunku zwierząt wzrosła w stosunku do liczby tych zwierząt z 31 grudnia 2011 r. o 120% i obecnie jest równa 8910. Ile zwierząt liczyła populacja tego gatunku w ostatnim dniu 2011 roku?

Zadanie 16. (NP17)
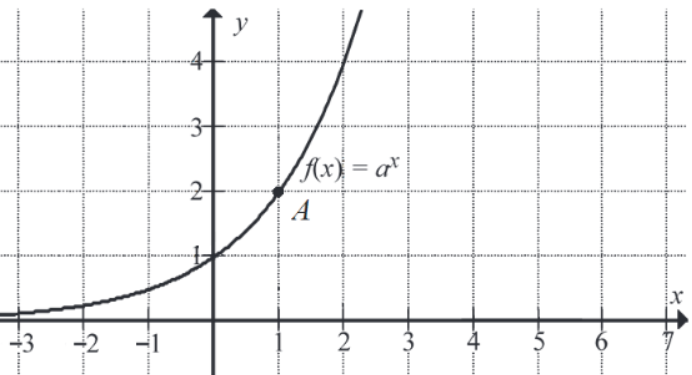
Na rysunku przedstawiono fragment wykresu funkcji wykładniczej f określonej wzorem f(x)=a^x. Punkt A=(1,2) należy do wykresu funkcji.

Podstawa a potęgi x jest równa:

Zadanie 17. (NP17)
Wykaż, że liczba 4²⁰¹⁷+42⁰¹⁸+4²⁰¹⁹+4²⁰²⁰ jest podzielna przez 17.

Zadanie 18. (NP18)
Liczba  jest równa:

Zadanie 19. (NP18)
Liczba   jest równa:

Zadanie 20. (NP18)
Dane są liczby a=3,6⋅10⁻¹² oraz b=2,4⋅10⁻²⁰. Wtedy iloraz jest równy:

Zadanie 21. (NP18)
Cena roweru po obniżce o 15% była równa 850 zł. Przed obniżką ten rower kosztował:

Zadanie 22. (NP18)
Udowodnij, że dla dowolnych liczb dodatnich a, b prawdziwa jest nierówność

Zadanie 23. (NP18)
Do wykresu funkcji wykładniczej, określonej dla każdej liczby rzeczywistej x wzorem f(x)=a^x (gdzie a>0 i a≠1), należy punkt P=(2,9). Oblicz a i zapisz zbiór wartości funkcji g, określonej wzorem g(x)=f(x)−2.

Zadanie 24. (SP15)
Cena pewnego towaru wraz z 7-procentowym podatkiem VAT jest równa 34 347 zł. Cena tego samego towaru wraz z 23-procentowym podatkiem VAT będzie równa

Zadanie 25. (SP15)
Najmniejszą liczbą całkowitą dodatnią spełniającą nierówność |x+4,5|≥6 jest

Zadanie 26. (SP15)
Liczba jest równa:

Zadanie 27. (SP15)
Liczba    jest równa

Zadanie 28. (SP14)
Jeżeli liczba 78 jest o 50% większa od liczby c, to:

Zadanie 29. (SP14)
Wartość wyrażenia  jest równa:

Zadanie 30. (SP14)
Suma jest równa

Zadanie 31. (SP14)
Dla każdej liczby x, spełniającej warunek −3<x<0, wyrażenie   jest równe

Zadanie 32. (SP14)
Liczba  jest równa:

Zadanie 33. (SP14)
Do wykresu funkcji, określonej dla wszystkich liczb rzeczywistych wzorem y=−2^x−2, należy punkt:

Zadanie 34. (SP14)
Udowodnij, że każda liczba całkowita k, która przy dzieleniu przez 7 daje resztę 2 ma tę własność, że reszta z dzielenia liczby 3k² przez 7 jest równa 5.

Zadanie 35. (SP13)
Wskaż rysunek, na którym zaznaczony jest zbiór wszystkich liczb rzeczywistych spełniających nierówność |x+4|<5.

Zadanie 36. (SP13)
Liczby a i b są dodatnie oraz 12% liczby a jest równe 15% liczby b. Stąd wynika, że a jest równe

Zadanie 37. (SP13)
Liczba jest równa

Zadanie 38. (SP13)
Najmniejszą liczbą całkowitą spełniającą nierówność    jest

Zadanie 39. (SP13)
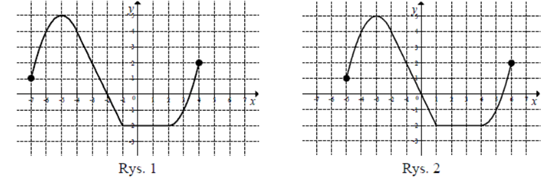
Na rysunku 1 przedstawiony jest wykres funkcji y=f(x) określonej dla x∈[−7,4].

 Rysunek 2 przedstawia wykres funkcji:

Zadanie 40. (SP13)
Liczba  jest równa:

Zadanie 41. (SP13)
Udowodnij, że dla dowolnych liczb rzeczywistych x,y,z takich, że x+y+z=0, prawdziwa jest nierówność xy+yz+zx≤0.

Możesz skorzystać z tożsamości (x+y+z)²=x²+y²+z²+2xy+2xz+2yz.

Zadanie 42. (SP13)
Wykaż, że liczba 6¹⁰⁰−2⋅6⁹⁹+10⋅6⁹⁸ jest podzielna przez 17.

Zadanie 43. (SP12)
Cenę nart obniżono o 20%, a po miesiącu nową cenę obniżono o dalsze 30%. W wyniku obu obniżek cena nart zmniejszyła się o:

Zadanie 44. (SP12)
Liczba   jest równa:

Zadanie 45. (SP12)
Liczba   jest równa:

Zadanie 46. (SP12)
Iloczyn jest równy:

Zadanie 47. (SP12)
Wskaż liczbę, która spełnia równanie |3x+1|=4x.

Zadanie 48. (SP12)
Uzasadnij, że jeśli liczby rzeczywiste a,b,c spełniają nierówności 0<a<b<c, to

Zadanie 49. (SP11)
Wskaż nierówność, którą spełnia liczba π:

Zadanie 50. (SP11)
Pierwsza rata, która stanowi 9% ceny roweru, jest równa 189 zł. Rower kosztuje:

Zadanie 51. (SP11)
Wyrażenie 5a²−10ab+15a jest równe iloczynowi:

Zadanie 52. (SP11)
Wyrażenie log₄(2x−1) jest określone dla wszystkich liczb x spełniających warunek:

Zadanie 53. (SP11)
Uzasadnij, że jeżeli a+b=1 i a²+b²=7, to a⁴+b⁴=31.

Zadanie 54. (SP10)
Wskaż rysunek, na którym jest przedstawiony zbiór rozwiązań nierówności |x+7|>5.

Zadanie 55. (SP10)
Spodnie po obniżce ceny o 30% kosztują 126 zł. Ile kosztowały spodnie przed obniżką?

Zadanie 56. (SP10)
Liczba  jest równa:

Zadanie 57. (SP10)
Liczba log₄8+log₄2 jest równa:

Zadanie 58. (SP10)
Wykaż, że jeśli a>0, to 

Zadanie 59. (SP10)
Wykaż, że liczba 3⁵⁴ jest rozwiązaniem równania 243¹¹−81¹⁴+7x=9²⁷

Zadanie 60. (SP08)
Rozwiąż równanie 4²³x − 32 ⁹x = 16⁴ ⋅(4⁴)⁴ . Zapisz rozwiązanie tego równania w postaci 2k , gdzie k  jest liczbą całkowitą.

Zadanie 61. (SP08)
Koncern paliwowy podnosił dwukrotnie w jednym tygodniu cenę benzyny, pierwszy raz o 10%, a drugi raz o 5%. Po obu tych podwyżkach jeden litr benzyny, wyprodukowanej przez ten koncern, kosztuje 4,62 zł. Oblicz cenę jednego litra benzyny przed omawianymi podwyżkami.

Zadanie 62. (SP07)
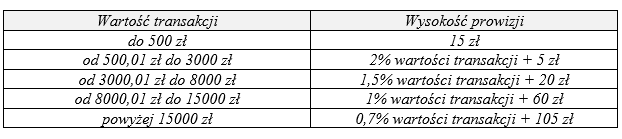
Wysokość prowizji, którą klient płaci w pewnym biurze maklerskim przy każdej zawieranej transakcji kupna lub sprzedaży akcji jest uzależniona od wartości transakcji. Zależność ta została przedstawiona w tabeli:

Klient zakupił za pośrednictwem tego biura maklerskiego 530 akcji w cenie 25 zł za jedną akcję. Po roku sprzedał wszystkie kupione akcje po 45 zł za jedną sztukę. Oblicz, ile zarobił na tych transakcjach po uwzględnieniu prowizji, które zapłacił.

Zadanie 63. (SP06)
Dane są zbiory:  . Zaznacz na osi liczbowej:

a) zbiór A,
b) zbiór B,
c) zbiór C= B/A.

Zadanie 63. (SP06)
Sklep sprowadza z hurtowni kurtki płacąc po 100 zł za sztukę i sprzedaje średnio 40 sztuk miesięcznie po 160 zł. Zaobserwowano, że każda kolejna obniżka ceny sprzedaży kurtki o 1 zł zwiększa sprzedaż miesięczną o 1 sztukę. Jaką cenę kurtki powinien ustalić sprzedawca, aby jego miesięczny zysk był największy.

Zadanie 64. (SP05)
Dane są zbiory liczb rzeczywistych:

Zapisz w postaci przedziałów liczbowych zbiory A, B, A∩ B oraz B − A.