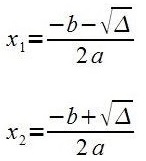Wielomiany

Wielomiany to wyrażenia algebraiczne składające się z zasady z wielu zmiennych, jednak można nimi nazwać także dwumiany lub trójmiany.

Przykład wyrażenia nazywanego wielomianem:

x12 + 2x5 – 3x3 + x2 + 8

Wielomiany nazywa się ze względu na stopień najwyższej występującej w nim potęgi, określając go jako wielomian stopnia n.

Przykład:

anxn + an−1xn−1 +…+ a2x2 + a1x + a0

gdzie  an, an−1, ….., a2, a1, a0 są określonymi liczbami rzeczywistymi oraz n ∊ N, a an ≠ 0.

Wyrażenie: x12 + 2x5 – 3x3 + x2 + 8, nazwiemy zatem wielomianem stopnia dwunastego.

Funkcje wielomianowe

Funkcjami wielomianowymi nazywa się wszystkie funkcje, których wzór określany jest poprzez wielomian. Najczęstszym stosowanym oznaczeniem funkcji wielomianowej jest litera W.

Przykład funkcji wielomianowej:

W(x) = 4x4 + 2x + 8

Obliczanie wartości wielomianu

Wartość wielomianów oblicza się tak samo jak w przypadku wartości funkcji czy wyrażeń algebraicznych, w miejsce x podstawiamy jedynie podaną liczbę.

Przykład:
Oblicz wartość liczbową podanego wielomianu W(x)= x3+4x-9, dla argumentu x=3
W miejsce x podstawiamy liczbę 3 i otrzymujemy:

W(3)= 33+3 ・4 – 9

W(3) = 9 +12 -9

W(3) = 12

Rozkładanie wielomianów na czynniki

Rozkładanie wielomianu na czynniki, to nic innego jak zapis postaci jego wzoru poprzez iloczyny nawiasów.

Przykłady wielomianów zapisanych w postaci ogólnej i iloczynowej:

Postać ogólna                        Postać iloczynowa

W(x) = x2-9                            W(x) = (x – 3) (x + 3)

W(x) = x2 + 5x+6                   W(x) = (x + 2) (x + 3)

W(x)= x3+ 5x                         W(x) = x(x2 + 5)

>> Chcesz dobrze zdać maturę z matematyki? Zobacz ebook  Matematyka część 2.

Do rozkładania wielomianów na czynniki wykorzystywane są takie metody jak:

  • wyciąganie wspólnego czynnika przed nawias,
  • wzory skróconego mnożenia,
  • wyliczanie delty,
  • grupowanie wyrazów.

Rozkładanie wielomianu na czynniki metodą wyciągania wspólnego czynnika przed nawias

Metoda ta umożliwia wyciągnięcie przed nawias zarówno liczb jak i liter oznaczających niewiadomą w wielomianie. Każde rozkładanie wielomianu na czynniki powinno być poprzedzone sprawdzeniem, czy nie można wyciągnąć ze składających się na wielomian jednomianów wspólnego czynnika przed nawias.

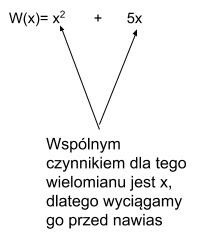
Przykład:

Otrzymujemy: W(x) = x (x + 5)

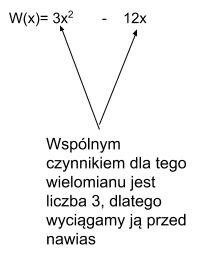
Otrzymujemy: W(x) = 3 (x2 -4x)

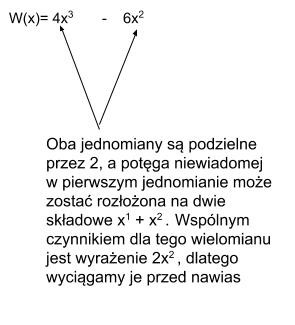
Otrzymujemy: W(x) = 2x2 (2x + 3)

Rozkładanie wielomianu na czynniki metodą wzorów skróconego mnożenia

W tej metodzie najczęściej wykorzystywany jest wzór skróconego mnożenia pod postacią:

a2 − b2 = (a−b) (a+b)

Zastosowanie tutaj mają jednak niemal wszystkie wzory skróconego mnożenia.

Przykłady:

W(x) = x2 – 9 po zastosowaniu wzoru skróconego mnożenia i otrzymujemy:

W(x) = (x – 3) (x + 3)

W(x) = x2 + 6x + 9 po zastosowaniu wzoru skróconego mnożenia otrzymujemy:

W(x) = (x + 3)2

Rozkładanie wielomianu na czynniki metodą delty

Metodę tę stosuje się do rozkładania na czynniki wielomianów drugiego stopnia w których nie można zastosować wzorów skróconego mnożenia.

Aby móc skorzystać z tej metody, należy przypomnieć sobie wzór na deltę, który brzmi następująco dla poniższego wyrażenia:

W(x) = ax2 + bx + c

△ = b2 – 4・a・c

W przypadku tej metody można spotkać się z trzema przypadkami:

  1. Delta jest mniejsza od zera – rozkład czynników nie jest możliwy,
  2. Delta jest większa od zera – istnieją dwa miejsca zerowe wielomianu, które można wyliczyć ze wzorów:

otrzymujemy wówczas postać iloczynowa wielomianu: W(x) = a(x – x1) (x – x2)

  1. Delta jest równa zeru- istnieje jedno miejsce zerowe wielomianu, które można wyliczyć ze wzoru: x_{1}=\frac{-b}{2a}   otrzymujemy wówczas postać iloczynowa wielomianu: W(x) = a(x – x1)2Przykład:Rozłóż wielomian W(x) = x2 – x – 6Na początku określamy współczynniki: a, b i c:a= 1 b= -1 c= -6Na ich podstawie liczymy delte ze wzoru:△= (-1) ・ 2 – 4 ・1・( -6) = 1 + 24 = 25 – delta wyszła większa od zera, czyli wielomian posiada dwa miejsca zerowe, które należy wyliczyć ze wzorów.

x_{1}=\frac{1-\sqrt{25}}{2}

x_{1}=\frac{1-5}{2}

x_{1}=-2

x_{2}=\frac{1+\sqrt{25}}{2}

x_{2}=\frac{1+5}{2}

x_{2}=3

Otrzymujemy wielomian: W(x) = 1・(x – 3)(x – (-2)) = (x -3 ) (x + 2)

Rozkładanie wielomianu na czynniki metodą grupowania wyrazów

Metodę tę stosuje się najczęściej w przypadku rozkładania na czynniki wielomianów stopnia czwartego oraz wyższych.

Metoda ta opiera się na zasadzie mówiącej, że jeśli wielomian składa się z czterech wyrazów, to można wyciągnąć przed nawias wspólny czynnik tylko z dwóch pierwszych wyrazów, a następnie wspólny czynnik z trzeciego i czwartego wyrazu.

Przykład:

W(x) = x3 + 4x2  + 2x + 8 = x2 (x + 4) + 2( x + 4)

Pierwsze dwa wyrażenia w tym przypadku pozwoliły na wyciąganie przed nawias x2, a wyrazy trzeci i czwarty pozwoliły na wyciągnięcie z nich przed nawias 2 . Jeśli podobnie jak w tym przykładzie w obu nawiasach mamy to samo wyrażenie, wielomian można uprościć jeszcze bardziej, wyciągając to, co w nawiasie przed niego i otrzymując wyrażenie:

W(x) = (x + 4) ( x2 + 2).

W przypadku kiedy w nawiasie otrzymamy wyrażenie które pozwala na zastosowanie delty lub wzorów skróconego mnożenia, należy je zastosować, aby uzyskać jak najprostszą postać wielomianu iloczynowego.

Dodawania i odejmowanie wielomianów

Wielomiany dodaje i odejmuje się w ten sam sposób jak inne wyrażenia algebraiczne. Dodając do siebie lub obejmując jednomiany tego samego stopnia, pamiętając przy tym, że przy odejmowaniu należy zmienić znak wszystkich odejmowanych wyrażeń na przeciwny.

Przykład:

Dodaj do siebie następujące wielomiany:

W(x) = 4x4 + 2x2 -11x + 3 ; G(x) = 2x4 + 6x2 -2x

W(x) + G(x) = 4x4 + 2x2 -11x + 3 + 2x4 + 6x2 – 2x = 6x4 +8x2 -13x + 3

Odejmij od siebie wielomiany:

W(x) = 4x4 + 2x2 -11x + 3 ; G(x) = 2x4 + 6x2 -2x

W(x) + G(x) =  4x4 + 2x2 -11x + 3 – (2x4 + 6x2 – 2x) = 4x4 + 2x2 -11x + 3 – 2x4 – 6x2 + 2x = 2x4 – 4x2 -9x + 3