Co to kwadrat?
Kwadrat definiuje się jako dwuwymiarową figurę o wszystkich bokach równej długości (czworokąt foremny). Wszystkie kąty między bokami kwadratu są równe i wynoszą 90°.
Własności kwadratu jako figury płaskiej:
- Suma kątów wewnętrznych w kwadracie jest równa 360°;
- Każdy kwadrat jest prostokątem;
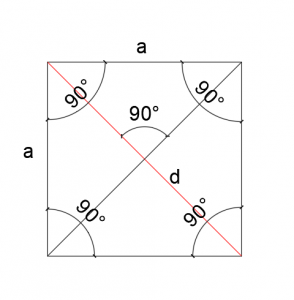
- Przekątne kwadratu są równe, przecinają się dokładnie w połowie i są względem siebie prostopadłe;
- Przekątna dzieli kwadrat na dwa trójkątny prostokątne o kątach wewnętrznych 90°, 45°, 45°;
- Kwadrat można opisać na kole, jak również wpisać w koło;
- Punkt przecięcia przekątnych jest równocześnie środkiem okręgu wpisanego i opisanego na kwadracie.
>> Chcesz dobrze zdać maturę z matematyki? Zobacz ebook Matematyka część 3.
Wzory na obliczanie wymiarów kwadratu
1. Pole kwadratu
Pole kwadratu liczymy ze wzoru:
P= a2,
gdzie a – to bok kwadratu
2. Obwód kwadratu
Obwód kwadratu to suma jego boków. Ponieważ w kwadracie wszystkie boki są równej długości, wzór na obwód tej figury prezentuje się następująco:
L= 4a
gdzie a- długość boku kwadratu
3. Przekątna kwadratu
d=
Długość przekątnej kwadratu wynika z własności trójkąta prostokątnego o kątach 90°, 45°, 45°.
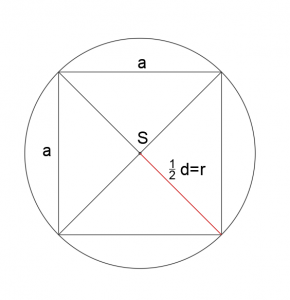
4. Promień okręgu opisanego na kwadracie
r=d
Promień okręgu opisanego na kwadracie wynosi połowę długości jego przekątnej.
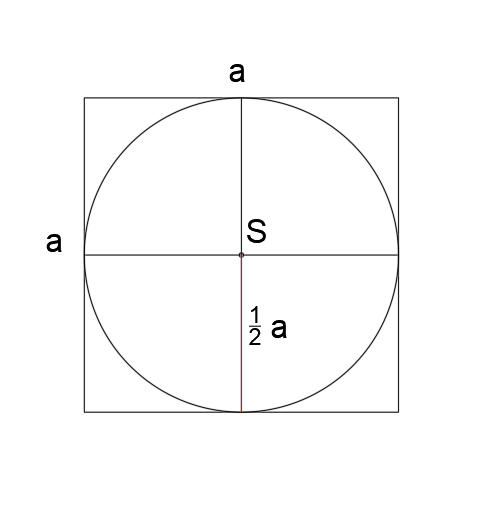
5. Promień okręgu wpisanego w kwadrat
r=a
Promień okręgu wpisanego kwadrat równy jest połowie długości boku kwadratu.