Czym się różni graniastosłup od prostopadłościanu?
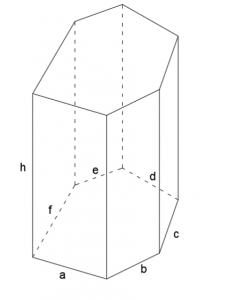
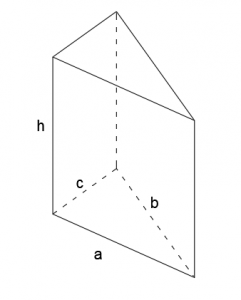
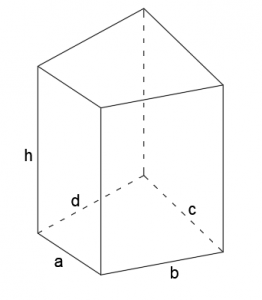
Graniastosłup jest przestrzenną bryłą. Wielościanem, który ma dwa takie same wielokąty w podstawie. Wszystkie krawędzie boczne graniastosłupa mają taką samą długość.
Graniastosłup prawidłowy definiuje się jako bryłę, która w podstawie ma figurę foremną (np. kwadrat, trójkąt równoboczny, sześciokąt foremny).
Prostopadłościan jest równoległościanem, którego wszystkie ściany stanowią prostokąty, a dwie jego dowolne ściany, mające wspólną krawędź są prostopadłe. Każda z przeciwległych ścian jest do siebie równoległa.
Krawędź wielościanu jest odcinkiem łączącym dwa wierzchołki bryły i tworzącym równocześnie wspólny bok przynajmniej dwóch ścian.
Wierzchołek wielościanu jest punktem wspólnym co najmniej trzech ścian wielościanu.
>> Chcesz dobrze zdać maturę z matematyki? Zobacz ebook Matematyka część 3.
Wzory na wymiary graniastosłupa
1. Objętość graniastosłupa jest liczona ze wzoru:
,
gdzie:
– pole powierzchni podstawy graniastosłupa,
H – wysokość, długość krawędzi graniastosłupa.
Pole powierzchni całkowitej graniastosłupa liczone jest wzorem:
,
gdzie:
– pole powierzchni podstawy graniastosłupa,
– pole powierzchni bocznej graniastosłupa (pola wszystkich ścian bryły).
2. Pole powierzchni podstawy graniastosłupa jest zależne od figury, która znajduje się w podstawie.
Pole powierzchni bocznej graniastosłupa – zależne jest od liczby krawędzi w podstawie bryły. Ta z kolei rzutuje na ilość ścian bocznych. Ściany boczne są z reguły prostokątami (graniastosłup prosty). Zdarza się, że ścianą boczną jest równoległobok. Mamy wówczas do czynienia z graniastosłupem pochyłym.
3. Pole powierzchni prostopadłościanu jest liczone wzorem:
,
gdzie:
a,b – krawędzie podstawy
c – krawędź boczna prostopadłościanu
4. Objętość prostopadłościanu jest dana wzorem:
,
gdzie:
a,b – krawędzie podstawy
c – krawędź boczna prostopadłościanu
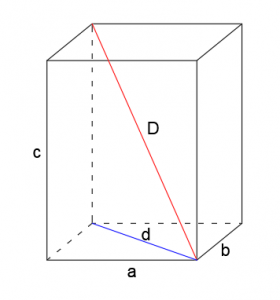
5. Długość przekątnej prostopadłościanu obliczyć można używając wzoru:
,
gdzie:
a,b – krawędzie podstawy,
c – krawędź boczna prostopadłościanu,
d – przekątna prostopadłościanu.