Właściwości funkcji wymiernej
Funkcja wymierna jest ilorazem dwóch funkcji wielomianowych P(x) oraz Q(x), przy czym wielomian Q(x) ≠0, jej postać jest następująca:
Funkcje wymierne mogą się składać z sumy kilku wyrażeń wymiernych. Wyrażenia te można upraszczać stosując działania matematyczne. Najprostszą postacią funkcji wymiernej jest , gdzie a jest wielomianem stopnia zero (funkcja stała) i a €R, natomiast x jest wielomianem pierwszego stopnia.
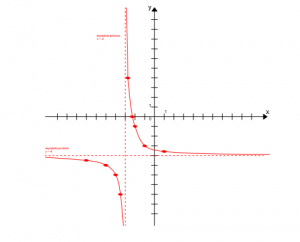
Wykresem funkcji wymiernej jest krzywa zwana hiperbolą. Składa się on z dwóch części, to przedziały określone przez dziedzinę funkcji.
Przykład:
>> Chcesz dobrze zdać maturę z matematyki? Zobacz ebook Matematyka część 2.
Szczególnym przypadkiem funkcji wymiernej jest funkcja homograficzna, którą opisuje następujący wzór:
gdzie ad-bc ≠0, oraz c≠0
Własności funkcji wymiernej
- Dziedziną funkcji wymiernej f(x) jest dziedzina funkcji P(x) pomniejszona o miejsca zerowy funkcji Q(x). Wyznaczamy pierwiastki wielomianu P(x), a następnie wyrzucamy je ze zbioru liczb rzeczywistych.
- Zbiorem wartości jest zbiór liczb rzeczywistych w wyjątkiem wartości w miejscu asymptoty poziomej.
- Miejsca zerowe funkcji wymiernej obliczamy w miejsce y podstawiając wartość 0. Pierwiastkiem jest rozwiązanie równania wymiernego. W przypadku funkcji wymiernej miejsce zerowe nie zawsze istnieje.
- Wykres funkcji wymiernej posiada asymptoty. Asymptota to prosta do której wykres się zbliża, lecz jej nie dotyka. Na hiperboli mamy asymptotę poziomą (y=0) oraz asymptotę pionową (x=0).
- Do określenia monotoniczności funkcji wymiernej należy narysować wykres tej funkcji oraz policzyć dziedzinę rozpatrywanej funkcji.