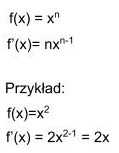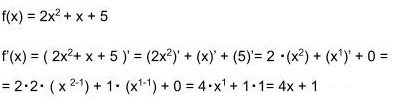Pochodne funkcji kwadratowej

Aby mówić o pochodnych funkcji kwadratowych określanych najczęściej jako f’(x), należy powrócić do głównej definicji pochodnych, która mówi, że funkcja f(x) jest określana w otoczeniu U punktu x0 oraz Δx≠0 i x0+Δx.

Iloraz różnicowy podanej funkcji f(x) w punkcie x0 dla przyrostu zmiennej określa się poprzez wyrażenie:

gdzie;
x0- punkt zerowy funkcji x,
Δx – przyrost zmiennej niezależnej od x

Natomiast pochodna funkcji f(x) w punkcie x0 nazywana jest granicą właściwą ilorazu różnicowego, gdy Δx dąży do 0.

>> Chcesz dobrze zdać maturę z matematyki? Zobacz ebook Matematyka część 2.

Na podstawie tej definicji zostały wyprowadzone wzory, które pozwalają na obliczanie pochodnych najpopularniejszych funkcji, w tym także funkcji kwadratowych.

Wzór na pochodną funkcji kwadratowej

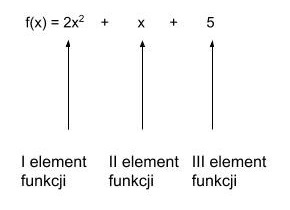
W przypadku złożonych funkcji kwadratowych pochodną takiej funkcji wylicza się na podstawie sumy pochodnej pierwszego elementu funkcji plus pochodna drugiego elementu funkcji plus pochodna trzeciego elementu funkcji.

Przykład: