Funkcja kwadratowa

Funkcja kwadratowa – zmiana własności funkcji, wzory, własności

Funkcja kwadratowa jest funkcją wielomianową drugiego stopnia. We wzorze funkcji kwadratowej mogą wystąpić zmienne w potędze pierwszej i drugiej (x, ) jak również stałe liczby.

Funkcję kwadratową można zapisać w postaci ogólnej, iloczynowej i kanonicznej.

Ogólny wzór funkcji kwadratowej, przyjmuje postać

f(x)=ax²+bx+c,

gdzie:
a, b, c – współczynniki liczbowe, a≠0

Współczynnik liczbowy jednomianu to liczba, która zapisywana jest przed zmienną. Np.

Dla 7x², współczynnikiem liczbowym jest liczba a=7;
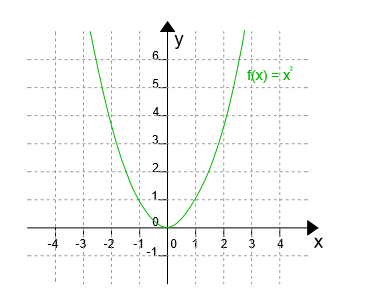
W przypadku funkcji f(x)=x², współczynniki liczbowe kształtują się następująco: a=1, b=0, c=0.

Postać kanoniczna funkcji kwadratowej

f(x) = a (x – p)²+ q,

gdzie:
a, p, q- współczynniki liczbowe, a≠0.

Współczynniki p, q są wierzchołkami funkcji kwadratowej. Aby je obliczyć należy zastosować wzory:

$p=-\frac{b}{2a}$

$q=\frac{-\Delta }{4a}$

Z postaci kanonicznej funkcji kwadratowej od razu można odczytać współrzędne wierzchołka.

Postać iloczynowa funkcji kwadratowej

Postać iloczynowa funkcji kwadratowej wygląda następująco:

f(x)= a (x-x₁) (x-x₂),

gdzie:
a≠0, a x₁, x₂ są miejscami zerowymi funkcji.

Postać iloczynowa funkcji kwadratowej nie istnieje, jeżeli funkcja nie ma miejsc zerowych.

Jeżeli $\Delta > 0$ , możemy obliczyć miejsca zerowe według wzorów: $x_1=-\frac{b^2+\sqrt{\Delta }}{2a}$ , $x_2=-\frac{b^2+\sqrt{\Delta }}{2a}$ .

Dzięki postaci iloczynowej funkcji kwadratowej od razu można wyznaczyć miejsca zerowe funkcji.

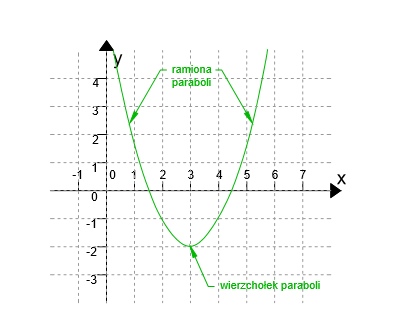
Wykres funkcji kwadratowej nosi nazwę paraboli. Każda parabola posiada wierzchołek i ramiona. Wykres funkcji kwadratowej jest obrazem paraboli, której wzór to f(x)=ax² i przesunięciu o wektor $\vec{u}=\left \langle \frac{-b}{2a}, \frac{-\Delta }{4a}\right \rangle$

>> Chcesz dobrze zdać maturę z matematyki? Zobacz ebook Matematyka część 2.

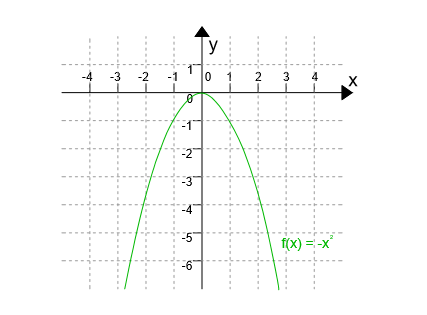
Parabola skierowana jest ramionami do góry, gdy współczynnik liczbowy a jest dodatni, gdy zaś jest ujemny parabola rysowana jest ramionami w dół.

Aby narysować poprawnie wykres funkcji kwadratowej trzeba wykonać następujące kroki:

Sprawdzić w którą stronę skierowane są ramiona paraboli (gdy a jest dodatnie, ramiona skierowane są w górę, gdy ujemne w dół);
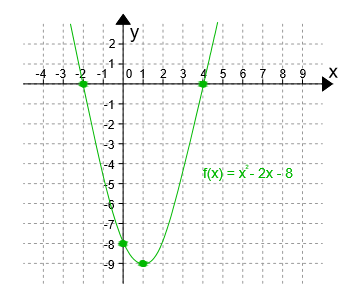
Obliczyć miejsca zerowe funkcji;
Obliczyć wierzchołek paraboli W(p,q);
Obliczyć punkt przecięcia z osią OY. Punk ten ma współrzędne (0, c).

Miejscem zerowym funkcji jest jej punkt przecięcia z osią OX. Aby zatem obliczyć miejsce zerowe funkcji, wzór funkcji należy przyrównać do zera. Poprawne wyliczanie miejsc zerowych funkcji kwadratowej, wymaga umiejętności rozwiazywania równań kwadratowych.

Miejsca zerowe funkcji nazywane są również jej pierwiastkami, a żeby je obliczyć wykorzystujemy następujące wzory:

1. Należy obliczyć wyróżnik: $\Delta =b^2-4ac$ . Po wyliczeniu wyróżnika zyskujemy wiedzę ile miejsc zerowych posiada dane równanie. Jeżeli:

$\Delta < 0$ , brak miejsc zerowych. Funkcja nie ma rozwiązania;
$\Delta =0$ , funkcja ma jedno miejsce zerowe. Istnieje jedno rozwiązanie funkcji.
$\Delta > 0$ , funkcja ma 2 miejsca zerowe.

2. W zależności od wyliczonej wartości wyróżnika stosowane są różne wzory, do obliczenia miejsc zerowych. W przypadku, gdy:

$\Delta =0$ , miejsce zerowe jest dane wzorem: $x_0=-\frac{b}{2a}$ ;
$\Delta > 0$ , pierwsze miejsce zerowe jest dane wzorem: $x_1=-\frac{b^2+\sqrt{\Delta }}{2a}$ , zaś drugie: $x_2=-\frac{b^2+\sqrt{\Delta }}{2a}$ .

Aby poprawnie narysować parabole niezbędna jest wiedza, w którym miejscu znajduje się wierzchołek paraboli. Wierzchołek paraboli ma współrzędne W(p,q), gdzie

$p=-\frac{b}{2a}$ ;

$q=\frac{-\Delta }{4a}$ .

Własności funkcji kwadratowej

Dziedziną funkcji jest zbiór liczb rzeczywistych $\mathbb{R}$
Zbiór wartości, dla a>0, stanowi przedział $y\in<\frac{-\Delta }{4a},\ +\infty )$ , dla a<0 $y\in(+\infty,\frac{-\Delta }{4a} >$ .
Monotoniczność – funkcja kwadratowa jest w pewnym przedziale funkcją rosnącą, a w pewnym malejącą.