Czym jest koło i okrąg?
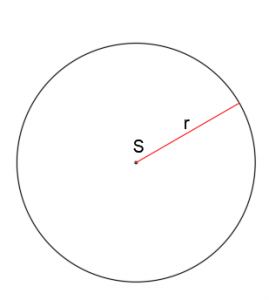
Okrąg – jest to zbiór wszystkich punktów na płaszczyźnie euklidesowej, których odległość od ustalonego punktu, będącego środkiem okręgu S jest taka sama i jest równa długości promienia okręgu r.
Koło – jest to zbiór wszystkich punktów na płaszczyźnie euklidesowej, których odległość od ustalonego punktu, będącego środkiem okręgu S, jest nie większa niż długość promienia koła r.
Podstawowe definicje – promień, cięnciwa, średnica
Promień- definiowany jako odcinek, który łączy środek okręgu S z dowolnym punktem na okręgu.
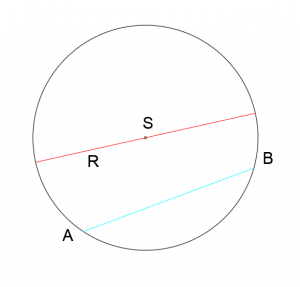
Cięciwa |AB| – odcinek przecinający okrąg lub koło w dowolnym miejscu. Ma dwa punkty wspólne z tarczą okręgu.
Średnica R – cięciwa przechodząca przez środek koła. Jej długość wynosi dwukrotność promienia koła.
>> Chcesz dobrze zdać maturę z matematyki? Zobacz ebook Matematyka część 3.
Własności koła i okręgu
- W okręgu wyróżniamy:
- kąt środkowy, czyli kąt, którego wierzchołek leży w środku okręgu, a ramionami są promienie,
- kąt wpisany – wierzchołek leży na okręgu, a ramionami są cięciwy;
- W okrąg można wpisać każdy rodzaj trójkąta;
- W okrąg można wpisać każdy wielokąt foremny, na każdym wielokącie foremnym można również okrąg opisać;
- Środek okręgu nie należy do okręgu.
Wzory na wymiary koła i okręgu
1. Długość okręgu
Długość okręgu jest obliczana następującym wzorem:
d=2πr
gdzie r – promień okręgu,
zaś π, to wartość stała wynosząca w przybliżeniu 3,14
2. Obwód koła
Obwód koła liczony jest ze wzoru na długość okręgu:
d=2πr
gdzie r – promień okręgu,
zaś π, to wartość stała wynosząca w przybliżeniu 3,14
3. Pole wycinka koła
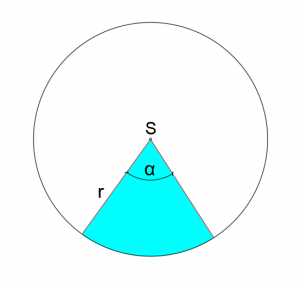
Wycinkiem koła jest pole ograniczone okręgiem (łukiem) i ramionami kąta środkowego.
S=
α- miara łukowa wycinka koła,
r- promień okręgu;
Analogiczny wzór dla miary stopniowej:
S=2πr
4. Pole koła
Pole koła liczone jest według wzoru:
P=πr2, gdzie
r- promień koła
π – stała, równa 3,14
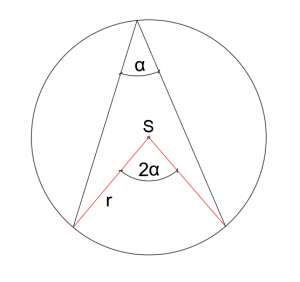
5. Kąty w okręgu
Miara kąta środkowego jest dwa razy większa od miary kąta wpisanego, opartego na tym samym łuku.
6. Liczba π
Liczba π jest definiowana jako stosunek obwodu koła do środka jego średnicy. Jest to stała. Wynosi w przybliżeniu 3,14.
7. Styczne i sieczne
Styczną jest prostą, która posiada z okręgiem jeden punkt wspólny, zwany punktem styczności. Jest prostopadła do promienia, który łączy punkt styczności ze środkiem okręgu.
Sieczna to prosta, posiadająca dwa punkty wspólne z okręgiem.
8. Wzajemne położenie prostej i okręgu
Położenie prostej i okręgu jest zależne od odległości środka okręgu od prostej. Odległość ta może być
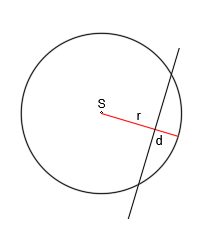
- Mniejsza od promienia – prosta jest wówczas sieczną okręgu;
r>d
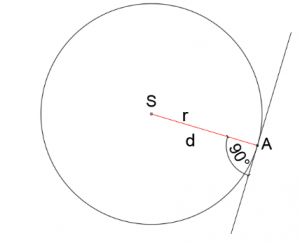
- Równa promieniowi – prosta jest styczną do okręgu;
r=d
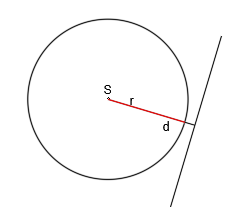
- Większa od promienia – prosta nie ma żadnych punktów wspólnych z okręgiem.
r<d