Czym jest sześcian?
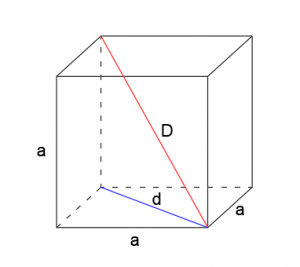
Sześcian jest szczególnym przypadkiem prostopadłościanu. Wszystkie jego ściany składają się z przystających kwadratów. Sześcian jest wielościanem foremnym. Składa się on z 12 krawędzi i 8 wierzchołków. Bryłę przecinają 4 przekątne. Ścianę sześcianu nazywa się jego podstawą.
Własności sześcianu
- Sześcian jest szczególnym przypadkiem wielościanu foremnego, którego wszystkie ściany są wielokątami foremnymi (kwadratami);
- W sześcian można wpisać kulę. Kulę na sześcianie można również opisać;
- Każdy sześcian jest prostopadłościanem, lecz nie każdy prostopadłościan jest sześcianem.
>> Chcesz dobrze zdać maturę z matematyki? Zobacz ebook Matematyka część 3.
Wzory na wymiary sześcianu
1. Pole powierzchni całkowitej
Pole powierzchni całkowitej sześcianu liczy się korzystając ze wzoru:
, gdzie
a – długość krawędzi sześcianu
2. Pole podstawy sześcianu
, gdzie
a – długość krawędzi sześcianu
Podstawą sześcianu jest jego ściana. Wszystkie ściany sześcianu są kwadratami.
3. Pole boczne sześcianu
, gdzie
a – długość krawędzi sześcianu
Pole boczne sześcianu to suma pól ścian sześcianu, składające się na jego
4. Długość przekątnej sześcianu
Długość przekątnej sześcianu można wyliczyć korzystając ze wzoru:
, gdzie
a – długość krawędzi sześcianu
Przekątną sześcianu wyprowadza się z trójkąta prostokątnego, którego przyprostokątne stanowią przekątna kwadratu i długość krawędzi sześcianu. Przekątna jest przeciwprostokątną tego trójkąta.
5. Długość przekątnej podstawy sześcianu
a – długość krawędzi sześcianu
Długość przekątnej podstawy sześcianu o krawędzi a, jest długością przekątnej kwadratu o boku a.
6. Objętość sześcianu
Objętość sześcianu liczona jest wzorem:
a – długość krawędzi sześcianu
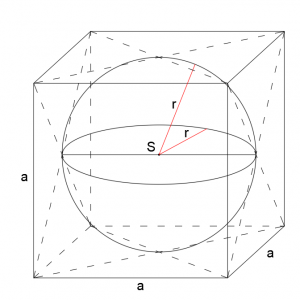
7. Kula wpisana i opisana na sześcianie
Długość promienia kuli wpisanej w sześcian liczony jest ze wzoru:
, gdzie
a – długość krawędzi sześcianu
Długość promienia kuli opisanej na sześcianie można obliczyć korzystając ze wzoru:
, gdzie
a – długość krawędzi sześcianu
D – przekątna sześcianu o boku długości a