Trygonometria trójkąta prostokątnego 

  1. Podstawowa definicja: Trygonometria jest to dział matematyki traktujący o zależnościach pomiędzy długościami boków a miarami kątów wewnętrznych w trójkątach. Funkcje trygonometryczne są rozszerzeniem tego działu. Służą, w oderwaniu od klasycznej geometrii w analizie matematycznej.
  1. Ogólna klasyfikacja funkcji trygonometrycznych: Pośród funkcji trygonometrycznych wymienia się sinus, cosinus, tangens i cotangens. Są to funkcje, działające na kątach. Są definiowane jako stosunku odpowiednich boków w trójkącie prostokątnym. Trygonometria umożliwia nam pomiar rzeczywistych wielkości przy pomocy prostych narzędzi pomiarowych, jak miarka i kątomierz.
  1. Funkcje trygonometryczne kąta ostrego:

a) Sinus

Sinusem kąta ostrego w trójkącie prostokątnym jest stosunek miar przeciwprostokątnej leżącej naprzeciw kąta ostrego do przeciwprostokątnej trójkąta prostokątnego.

sin\alpha=\frac{a}{c}

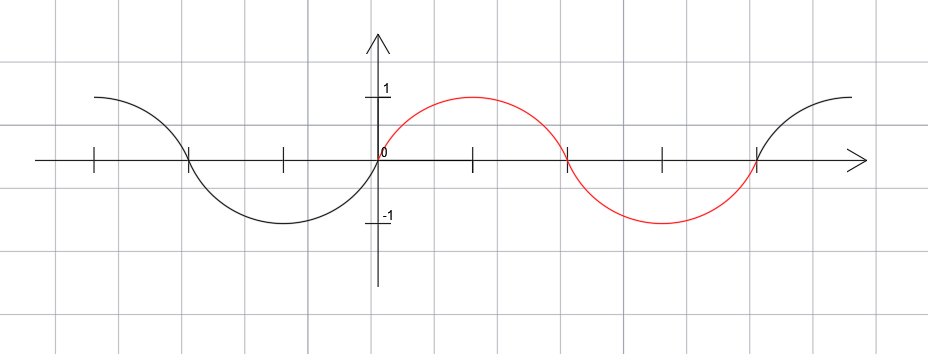
Wykresem funkcji sinus jest sinusoida.

f(x)=sinx

Sinus jest to funkcja okresowa, o okresie podstawowym równym T =2π.

Dziedziną sinusa jest zbiór licz rzeczywistych. Zbiór jego wartości zawiera się w przedziale <-1;1>. Funkcja sinus jest przedziałami monotoniczna. Rośnie w przedziałach <-\frac{\pi }{2}+2k\pi ; \frac{\pi}{2}+2k\pi> i maleje w  <\frac{\pi }{2}+2k\pi ; \frac{3\pi}{2}+2k\pi>, gdzie k\in \mathbb{Z}. Funkcja jest nieparzysta i nie jest równowartościowa.

b) Cosinus

Cosinusem kąta ostrego w trójkącie prostokątnym jest stosunek miar przyprostokątnej leżącej przy kącie ostrym do przeciwprostokątnej trójkąta prostokątnego.

cos\alpha =\frac{b}{c}

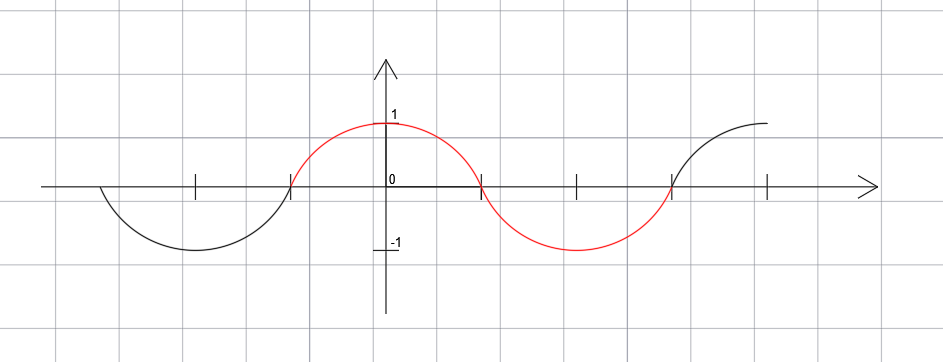
Wykresem funkcji sinus jest cosinusoida.

f(x)=cosx

>> Chcesz dobrze zdać maturę z matematyki? Zobacz ebook  Matematyka część 3.

Sinus jest to funkcja okresowa, o okresie podstawowym równym T =2π.

Dziedziną sinusa jest zbiór licz rzeczywistych. Zbiór jego wartości zawiera się w przedziale <-1;1>. Funkcja cosinus jest przedziałami monotoniczna. Rośnie w przedziałach <2k\pi ; \pi+2k\pi> i maleje w  <\pi +2k\pi ; 2\pi +2k\pi>, gdzie k\in\mathbb{Z}. Funkcja jest nieparzysta i nie jest równowartościowa.

c) Tangens

Tangensem kąta ostrego trójkąta prostokątnego jest stosunek miar przyprostokątnej leżącej naprzeciw kąta ostrego do przeciwprostokątnej trójkąta prostokątnego.

tg\alpha=\frac{a}{b}

f(x)=tgx

Tangens jest to funkcja okresowa, o okresie podstawowym równym T =π.

Dziedziną tangensa jest zbiór licz rzeczywistych z wyłączeniem  \frac{\pi}{2}+k\pi. Zbiór jego wartości jest zbiorem liczb rzeczywistych. Tangens posiada miejsca zerowe w x0= kπ. Funkcja tangens jest przedziałami monotoniczna. Rośnie w przedziałach <-\frac{\pi}{2}+k\pi;\frac{\pi}{2}+k\pi>, gdzie k\in\mathbb{Z}. Funkcja jest nieparzysta i nie jest równowartościowa.

d) Cotangens

Cotangensem kąta ostrego trójkąta prostokątnego jest stosunek miar długości przyprostokątnej leżącej przy kącie ostrym do przeciwprostokątnej trójkąta prostokątnego.

ctg\alpha=\frac{b}{a}

f(x)=tgx

Cotangens jest to funkcja okresowa, o okresie podstawowym równym T =π. Dziedziną cotangensa jest zbiór licz rzeczywistych z wyłączeniem okresu kπ. Zbiór jego wartości jest zbiorem liczb rzeczywistych. Cotangens posiada miejsca zerowe w x_0=\frac{\pi}{2}+k\pi. Funkcja cotangens jest przedziałami monotoniczna. Maleje w przedziałach <k\pi ; \pi + k\pi, gdzie k\in \mathbb{Z}. Funkcja jest nieparzysta i nie jest równowartościowa.

Funkcje trygonometryczne kąta ostrego w trójkącie prostokątnym są zawsze dodatnie. Wynika to z faktu, iż są one stosunkiem odpowiednich boków trójkąta prostokątnego. Długość boku nigdy nie będzie wartością ujemną.

Tangens i cotangens są wartościami odwrotnymi, stąd:

ctg\alpha\cdot ctg \alpha=1, albo ctg\alpha=\frac{1}{tg\alpha}

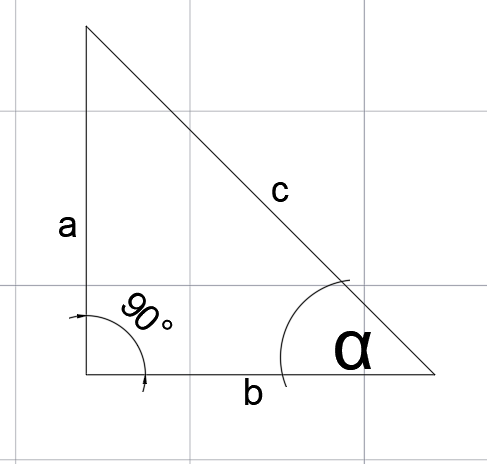
W trójkącie prostokątnym o bokach a, b, c i kątach 90°, α, β.

sinα=cosβ=\frac{a}{c}

cosα=sinβ=\frac{b}{c}

tgα=ctgβ=\frac{a}{b}

ctgα=tgβ=\frac{b}{a}

  1. Wzory redukcyjne

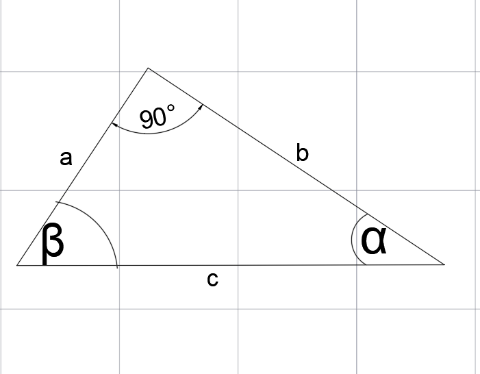
Mając trójkąt prostokątny

Suma miar kątów wewnętrznych w trójkącie wynosi 180°, zatem

β=90°-α

zatem:

sinα=cos(90°-α)

cosα=sin(90°-α)

tgα=ctg(90°-α)

ctgα=tg(90°-α)

dla k\in\mathbb{Z}:

sin(α + k*360°)= sinα

cos(α + k*360°)= cosα

tg(α + k*360°)= tgα

ctg(α + k*360°)= ctgα

W przypadku tangensa i cotangensa

tg(α + k*180°)= tgα

ctg(α + k*180°)= ctgα

Wzory redukcyjne umożliwiają nam obliczanie wartości dowolnego kąta, znając funkcje trygonometryczne kąta ostrego. Zestawienie wzorów redukcyjnych zamieszono poniżej:

sin(90∘+α)=cosα

cos(90∘+α)=−sinαt

g(90∘+α)=−ctgα

ctg(90∘+α)=−tgα

 sin(90∘−α)=cosα

cos(90∘−α)=sinα

tg(90∘−α)=ctgα

ctg(90∘−α)=tgα
sin(180∘+α)=−sinα

cos(180∘+α)=−cosα

tg(180∘+α)=tgα

ctg(180∘+α)=ctgα

 sin(180∘−α)=sinα

cos(180∘−α)=−cosα

tg(180∘−α)=−tgα

ctg(180∘−α)=−ctgα
sin(270∘+α)=−cosα

cos(270∘+α)=sinα

tg(270∘+α)=−ctgα

ctg(270∘+α)=−tgα

 sin(270∘−α)=−cosα

cos(270∘−α)=−sinα

tg(270∘−α)=ctgα

ctg(270∘−α)=tgα
sin(360∘+α)=sinα

cos(360∘+α)=cosα

tg(360∘+α)=tgα

ctg(360∘+α)=ctgα

 sin(360∘−α)=−sinα

cos(360∘−α)=cosα

tg(360∘−α)=−tgα

ctg(360∘−α)=−ctgα

W każdym trójkącie prostokątnym zachodzą następujące równania i związki:

  1. sin2α + cos2α = 1 jest to tzw. Jedynka trygonometryczna.
  2. tgα⋅ctgα=1
  3. tg\alpha=\frac{sin\alpha}{cos\alpha}
  4. tg\alpha=\frac{cos\alpha}{sin\alpha}

Dzięki zastosowaniu powyższych wzorów, możemy obliczyć każdą funkcję trygonometryczną, znając wartość jednej z nich.

Wartości funkcji trygonometrycznych są dane w tabeli wartości. Wartość najczęściej występujących kątów:

α

0°

30°

45°

60°

90°

sinα

0

 \frac{1}{2} \frac{\sqrt{2}}{2} \frac{\sqrt{3}}{2}

1

cosα

1

 \frac{\sqrt{3}}{2} \frac{\sqrt{2}}{2} \frac{1}{2}

0

tgα

0

 \frac{\sqrt{3}}{3}

1

 \sqrt{3}

nie istnieje

ctgα

nie istnieje

 \sqrt{3}

1

 \frac{\sqrt{3}}{3}

o
  1. Miary kątów

Kątem jednostkowym jest kąt, któremu przyporządkowujemy liczbę 1. Jeżeli więc kąt mierzymy w stopniach, jest to kat o mierze 1°.

Miarą kąta jest więc liczbą, która określa ile razy w danym kącie mieści się kąt jednostkowy. W matematyce stosuje się miarę łukową. Warto nadmienić, że miara kąta to nie to samo, co kąt. Kąt jest zbiorem punktów, fragmentem płaszczyzny ograniczonym ramionami kąta. Miara kąta zaś, jest jedynie atrybutem kąta. Wyróżniamy kąty:

Nazwa kąta Miara kąta
Zerowy 0°
Prosty 90°
Półpełny 180°
Pełny 360°
Ostry <90°
Rozwarty >90°
wypukły ≤180°
wklęsły ≥180°

Najczęściej w matematyce wstępują kąty z przedziału zamkniętego <0°; 360°>.

>> Chcesz dobrze zdać maturę z matematyki? Zobacz ebook  Matematyka część 3.

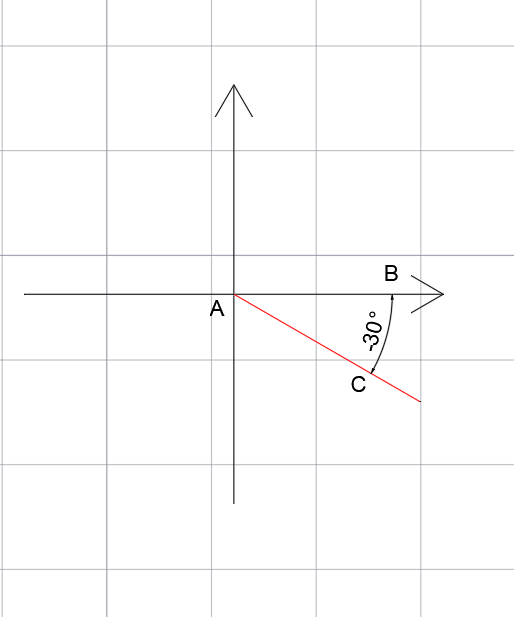
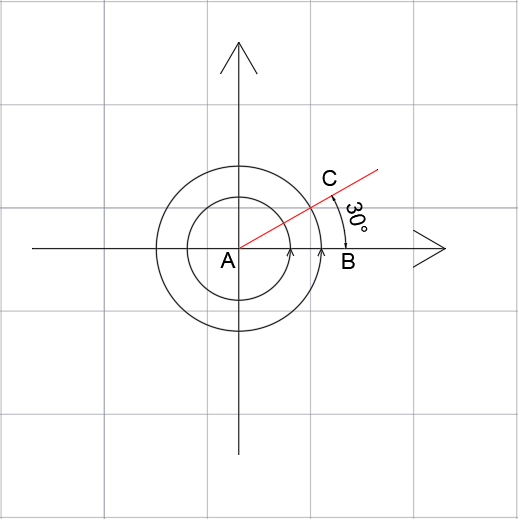
Kąty o mierze dodatniej powstają poprzez obrót półprostej AB wokół punktu A. Wynikiem obrotu półprostej w kierunku przeciwnym do ruchu wskazówek zegara są kąty o mierze dodatniej. Obrót w przeciwnym kierunku powoduje powstania kąta o mierze ujemnej.

Obrót półprostej AB nie musi zamykać się na 360°. Półprostą można obrócić kilka razy. Dla przykładu w wyniku dwukrotnego obrotu półprostą i obrotem o dodatkowych 47° otrzymujemy kąt o mierze 2*360°+47° = 767°.

Kąty można ze sobą utożsamić. Jeżeli ramię kąta α pokrywa się z ramieniem kąta β kąty utożsamiamy ze sobą. Jeżeli miara kąta α wynosi x, wówczas miara kąta β wynosi 360°+x.

Miara łukowa kąta

Poza popularną miarą stopniową kąta, wyróżniamy również miarę łukową. O ile kąty w przypadku miary stopniowej podajemy w stopniach, o tyle przy mierze łukowej, w radianach.

Miara stopniowa:

  • Podstawową jednostką jest 1°;
  • Kąt pełny wynosi 360°;
  • Oparty jest na systemie sześćdziesiętnym. 1°=60’=36000”

Miara łukowa kąta

  • Podstawową jednostką jest 1 radian;
  • Kąt pełny ma miarę 2π;
  • Oparty na systemie dziesiętnym.

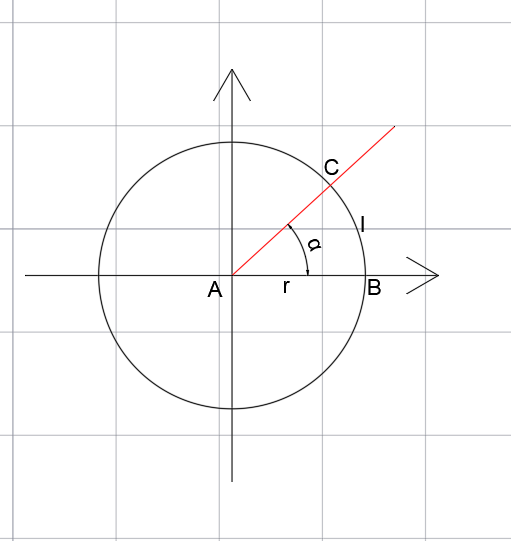
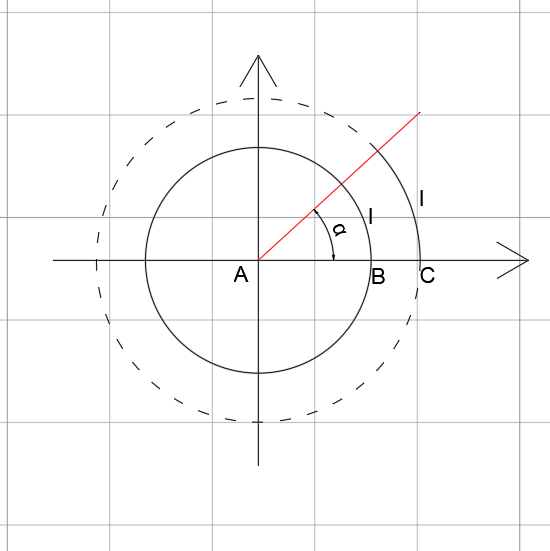
Miarą łukową kąta α jest stosunek  długości łuku, oznaczonego symbolem l do długości ramienia r.

Ponieważ długość łuku jest proporcjonalna do długości ramienia, miara łukowa kąta nie zależy od długości promienia.

\frac{l}{\left | AB \right |}=\frac{L}{\left | AC \right |}

Zamiana miary stopniowej na radialną zachodzi poprzez wzór:

\alpha (rad)=\frac{\alpha ^{\circ}\cdot \pi}{180^{\circ}}rad

I w odwrotnym kierunku

1rad=\frac{180^{\circ}}{\pi} .

Funkcje trygonometryczne dla dowolnego kąta

Aby obliczyć funkcje trygonometryczne dla dowolnego kąta, w układzie współrzędnych narysować należy okrąg o promieniu r i kącie środkowym α. Ramię kąta wyznaczone zostanie przez punkt P= (x,y).

Ogólne funkcje trygonometryczne wyglądają następująco:

sin\alpha=\frac{y}{r}

cos\alpha=\frac{x}{r}

tg\alpha=\frac{y}{x}

ctg\alpha=\frac{x}{y}.

W funkcjach trygonometrycznych pojawiają się również wartości ujemne. Znak przy każdej funkcji trygonometrycznej zależy od ćwiartki układu współrzędnych, w której się znajduje.

W pierwszej wszystkie są dodatnie,

W drugiej tylko sinus,

W trzeciej tangens i cotangens,

A w czwartej cosinus.

  1. Zestawienie przydatnych wzorów trygonometrycznych

Funkcje trygonometryczne sumy i różnicy kątów:

sin(α+β)=sinαcosβ+sinβcosα

sin(α−β)=sinαcosβ−sinβcosα

cos(α+β)=cosαcosβ−sinαsinβ

cos(α−β)=cosαcosβ+sinαsinβ

tg(\alpha+\beta)=\frac{tg\alpha+tg\beta}{1-tg\alpha tg\beta}

tg(\alpha-\beta)=\frac{tg\alpha-tg\beta}{1+tg\alpha tg\beta}

ctg(\alpha+\beta)=\frac{ctg\alpha ctg\beta-1}{ctg\alpha +ctg\beta}

ctg(\alpha-\beta)=\frac{ctg\alpha ctg\beta=1}{ctg\alpha -ctg\beta}

Funkcje trygonometryczne kąta podwojonego:

sin2α=2sinαcosα=\frac{2tg\alpha}{1+tg^2\alpha}

cos2α=cosα−sin α=2cos2α−1

tg2α=2 tgα1−tg2α=2ctgα−tgα

ctg2α=ctg2α−12 ctgα=\frac{ctg\alpha - tg\alpha}{2}

Funkcje trygonometryczne kąta potrojonego:

sin3α=−4sin3α+3sinα

cos3α=4cos3α−3cosα

tg3α=\frac{3tg\alpha - tg3\alpha}{1-3tg2\alpha}

ctg3α=\frac{3ctg^2\alpha-1}{ctg3\alpha-3ctg\alpha}

 

Sumy i różnice funkcji trygonometrycznych:

sin\alpha+sin\beta=2sin\frac{\alpha+\beta}{2}cos\frac{\alpha-\beta}{2}

sin\alpha-sin\beta=2cos\frac{\alpha+\beta}{2}sin\frac{\alpha-\beta}{2}

cos\alpha+cos\beta=2cos\frac{\alpha+\beta}{2}cos\frac{\alpha-\beta}{2}

cos\alpha-cos\beta=-2sin\frac{\alpha+\beta}{2}cos\frac{\alpha-\beta}{2}

tg\alpha+tg\beta=\frac{sin(\alpha+\beta)}{cos\alpha cos\beta}

tg\alpha-tg\beta=\frac{sin(\alpha-\beta)}{sin\alpha sin\beta}

ctg\alpha-ctg\beta=\frac{sin(\beta+\alpha)}{sin\alpha sin\beta}

ctg\alpha+ctg\beta=\frac{sin(\beta-\alpha)}{sin\alpha sin\beta}

cosα+sinα= \sqrt{2}sin(45°+α)=\sqrt{2}cos(45°-α)

cosα−sinα=\sqrt{2}cos(45°+α)=\sqrt{2}sin(45°-α)

Sumy i różnice jedności z funkcjami trygonometrycznymi:

1+sin\alpha=2sin^2(45^{\circ}+\frac{\alpha}{2})=2cos^2(45^{\circ}+\frac{\alpha}{2})

1-sin\alpha=2sin^2(45^{\circ}+\frac{\alpha}{2})=2cos^2(45^{\circ}+\frac{\alpha}{2})

1+cos\alpha=2cos^2\frac{\alpha}{2}

1-cos\alpha=2sin^2\frac{\alpha}{2}

1+tg2\alpha=\frac{1}{cos2\alpha}