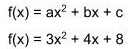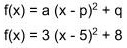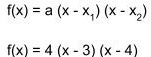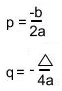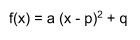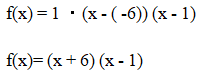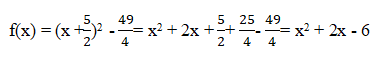Zmiana postaci funkcji kwadratowych
Funkcje kwadratowe mogą występować pod wieloma postaciami, zazwyczaj w wykonywaniu działań dąży się zawsze do przedstawienia funkcji kwadratowej w jak najłatwiejszy sposób. Wyróżnia się jednak trzy najpopularniejsze i najczęściej stosowane postacie funkcji, a są nimi:
- postać ogólna,
Przykład:
- postać kanoniczna,
Przykład:
- postać iloczynowa.
Przykład:
>> Chcesz dobrze zdać maturę z matematyki? Zobacz ebook Matematyka część 2.
Zamiana postaci ogólnej funkcji kwadratowej na kanoniczną i iloczynową
Do zmiany postaci funkcji w dowolną inną postać, niezbędna jest znajomość właściwych wzorów, które zostaną podane w poniższych przykładach.
Zamiana postaci funkcji ogólnej na kanoniczną
Aby zmienić postać ogólną funkcji kwadratowej na postać kanoniczną, należy obliczyć p oraz q, korzystając z poniższych wzorów:
i podstawić je pod wzór postaci kanonicznej:
Przykład:
Przekształć wzór funkcji f(x) = x2 + 5x – 6 na postać kanoniczną
Wypisujemy współczynniki liczbowe:
a = 1
b = 5
c = -6
Następnie obliczamy deltę ze wzoru Δ = b2−4ac
Δ = 52 – 4 ・1 ・ (-6) = 25 + 24 = 49
Potem wyliczamy ze wzorów p oraz q:
Podstawiając do wzoru, zapisujemy postać kanoniczną funkcji:
Zamiana postaci funkcji kanonicznej na ogólną
Chcąc zamienić, postać funkcji kanonicznej w ogólną, wystarczy obliczyć wyrażenie i je uprościć.
Z takiej postaci możemy wyodrębnić współczynniki liczbowe b oraz c, aby uzyskać, postać iloczynową, gdzie:
b= – 2ap
c = ap2 +q
Przykład na liczbach:
Zamiana postaci funkcji iloczynowej w ogólną
Chcąc zmienić, postać funkcji iloczynowej na ogólną, wystarczy jedynie wymnożyć nawiasy, jak na przykładzie poniżej.
Przykład:
f(x)= (x +6) (x – 1) = x2 – x+ 6x – 6 = x2 + 5x – 6