Funkcje liniowe
Czym jest funkcja liniowa? Funkcję f nazywamy liniową, gdy określona jest następującym wzorem f(x)=ax+b. Wykresem funkcji liniowej jest linia prosta. Wyznaczenie punktów i narysowanie wykresu sprowadza się jedynie do wybrania ze zbioru liczb rzeczywistych dowolnej liczby ( najlepiej 1 lub 0) będącej jednocześnie pierwszą współrzędną punktu i podstawieniu do wzoru w miejsce x, wyznaczając druga współrzędną punktu. Do narysowania wykresu linii prostej należy wyznaczyć minimum dwa punkty.
Funkcja liniowa może być zapisana w postaci kierunkowej lub ogólnej. Istnieje jeszcze postać odcinkowa, ale nie jest popularna i rzadko stosowana.
Funkcja liniowa wzory:
Postać kierunkowa funkcji liniowej jest opisana następującym wzorem:
Z kolei postać ogólną funkcji liniowej opisuje następujący wzór:
Natomiast postać odcinkową opisuje następujący wzór:
Przejście z jednej postaci na drugą polega jedynie na przekształceniach funkcji.
Dziedzina funkcji liniowej to zbiór liczb rzeczywistych. Oznacza to, że za x możemy podstawić dowolną liczbę. Zbiorem wartości funkcji liniowej z wyjątkiem funkcji stałej również zbiór liczb rzeczywistych. Natomiast w przypadku funkcji stałej, wartość zbioru wartości określona jest przez wzór funkcji liniowej.
>> Chcesz dobrze zdać maturę z matematyki? Zobacz ebook Matematyka część 2.
W skład funkcji liniowej w postaci kierunkowej wchodzi współczynnik a i b, pierwszy z nich nazywamy współczynnikiem kierunkowym natomiast drugi, wyrazem wolnym. Współczynnik kierunkowy odpowiada za monotoniczność funkcji liniowej oraz kąt nachylenia wykresu funkcji do osi X, można go obliczyć z następującego wzoru:
Gdzie (x1, y1) i (x2, y2) określają współrzędne dwóch punktów należących do wykresu funkcji liniowej.
Współczynnik b decyduje o punkcie przecięcia się wykresu prostej z osią Y.
Własności funkcji liniowej
Poniżej przedstawiamy własności funkcji liniowej. Miejsce zerowe funkcji jest to miejsce przecięcia się funkcji liniowej z osią X. Funkcja liniowa może mieć:
- Jedno miejsce zerowe, gdy przecina się z osią X
- Nieskończenie wiele miejsc zerowych, gdy opisuje ją równanie y=0
- Żadnego miejsca zerowego, gdy jest stała y≠ 0
Pierwszym sposobem na wyznaczenie miejsca zerowego funkcji liniowej jest podstawienie za y zera i obliczenie prostego równania z jedną niewiadomą x, to właśnie ten x jest miejscem zerowym funkcji.
Drugi sposób opiera się na zastosowaniu wzoru, wykorzystującego współczynniki występujące w postaci kierunkowej i ma następującą postać:
Przykłady.
– Sprawdzenie, czy dany punkt należy do wykresu funkcji liniowej. Należy podstawić jego współrzędne do wzoru funkcji i wykonać obliczenia. Jeżeli lewa strona równa jest prawej stronie równania, to dany punkt należy do wykresu funkcji.
Przykład.
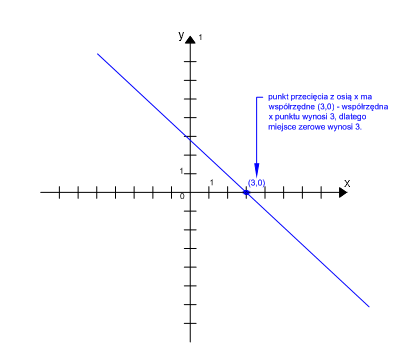
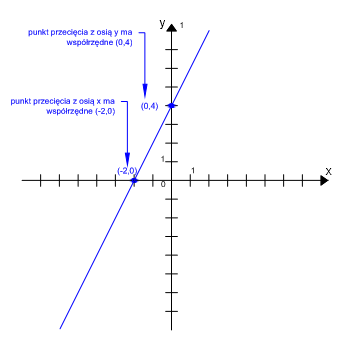
– Punkty przecięcia z osiami:
- Aby wyznaczyć punkt przecięcia z osią Y, należy za x podstawić 0 i obliczyć y
- Aby wyznaczyć punkt przecięcia z osią X (miejsce zerowe), należy za y podstawić 0 i obliczyć x.
– Prosta równoległa i prostopadła
- Dane proste są do siebie równoległe, jeżeli posiadają taki sam współczynnik kierunkowy a, funkcji liniowej y=ax +b
- Dane proste są do siebie prostopadłe, jeżeli współczynnik kierunkowy jednej z nich wynosi a, natomiast drugiej
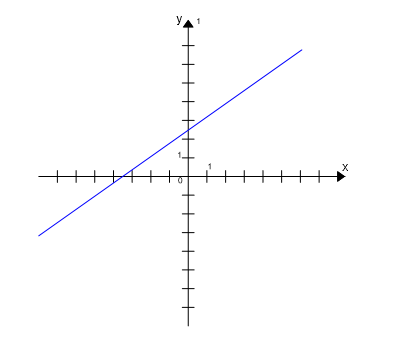
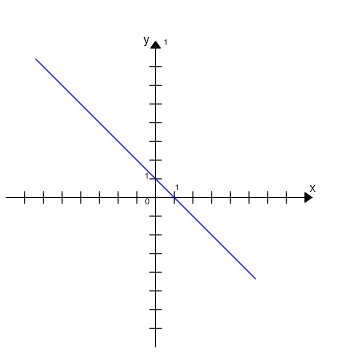
– Monotoniczność funkcji liniowej określa czy dana funkcja jest rosnąca, malejąca lub stała. Można ją określić z wykresu funkcji liniowej, czytając wykres od lewej do prawej, lub za pomocą współczynnika kierunkowego funkcji zapisanej w postaci kierunkowej:
- Jeżeli a < 0 to funkcja jest malejąca,
- Jeżeli a > 0 to funkcja jest rosnąca
- Jeżeli a = 0 to funkcja jest stała.
Monotoniczność funkcji daje się stwierdzić po wyglądzie wizualnym jej wykresu (patrz przykłady poniżej).
Przykład. Wykres funkcji rosnącej
Przykład. Wykres funkcji malejącej
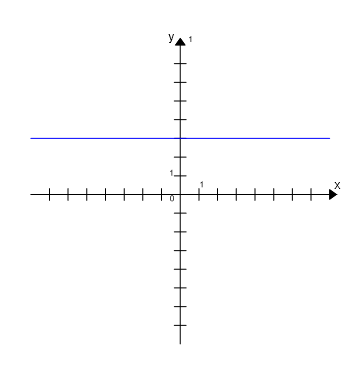
Przykład. Wykres funkcji stałej
Mamy nadzieję, że nasz artykuł okazał się przydatny, jeśli chcieliście przypomnieć sobie najważniejsze informacje na temat funkcji liniowej. Na naszej stronie znajdziecie także wiadomości utrwalające wiedzę na temat figur geometrycznych, takich jak trapez czy romb.
Zapewniamy również profesjonalnie przygotowane kursy maturalne, dzięki którym utrwalisz swoją wiedzę.Zachęcamy do skorzystania z naszej oferty.