Romb – definicja

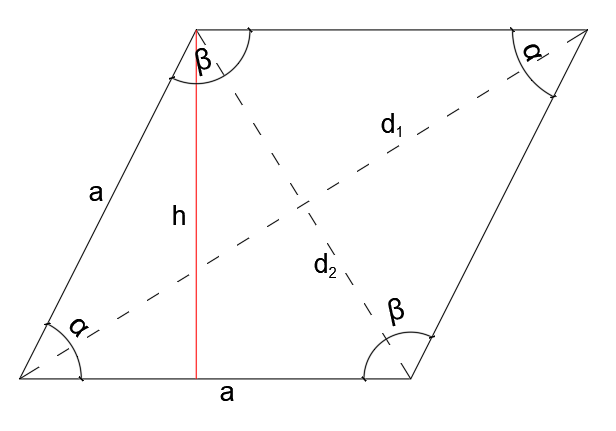
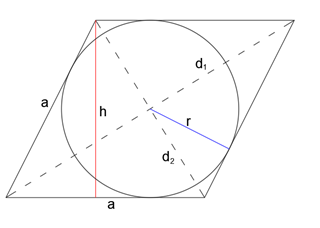
Romb jest czworokątem, który ma wszystkie boki równej długości. To figura wypukła. Punkt przecięcia przekątnych jest środkiem okręgu wpisanego, gdzie promień jest połową wysokości rombu. Suma miar kątków w rombie wynosi 360°. Przekątne dzielą romb na przystające trójkąty równoramienne.

Własności rombu

– czworokąt o wszystkich bokach równych;

– ma dwie pory kątów o tej samej mierze;

– suma sąsiadujących ze sobą kątów wynosi 180°;

– romb ma dwie osie symetrii;

– przekątne rombu przecinają się pod kątem prostym i dzielą się dokładnie na połowę;

– romb jest równoległobokiem. Szczególnym przypadkiem rombu jest kwadrat.

>> Chcesz dobrze zdać maturę z matematyki? Zobacz ebook  Matematyka część 3.

Wzory na wymiary rombu

1. Pole rombu – wzór

Pole rombu oblicza się według wzoru

PP=\frac{d_1 \cdot d_2}{2}=a\cdot h=a^2sin\alpha =\frac{h^2}{sin\alpha},

gdzie:
d1, d2 – przekątne rombu
c – Długość boku rombu
h – wysokość rombu

2. Obwód rombu

Obwód rombu liczony jest ze wzoru:

L= 4a,

gdzie:
a- Długość boku rombu

3. Długość przekątnych rombu

Wzór na obliczenie dłuższej przekątnej rombu wygląda następująco:

f=2a\cdot cos \frac{\alpha}{2}=\frac{2\cdot P}{d},

gdzie:
a – Długość boku rombu,
f – długość dłuższej przekątnej rombu;
d – długość krótszej przekątnej rombu;
P – pole powierzchni rombu
α – miara kąta wewnętrznego rombu

4. Długość krótszej przekątnej rombu obliczany jest ze wzoru:

d=2a\cdot sin\frac{\alpha }{2}=\frac{2\cdot P}{f},

gdzie:
a – Długość boku rombu,


f – długość dłuższej przekątnej rombu;
d – długość krótszej przekątnej rombu;
P – pole powierzchni rombu
α – miara kąta wewnętrznego rombu

Pole rombu można obliczyć również biorąc pod uwagę promień okręgu wpisanego w romb. Wzór kształtuje się następująco.

P=2a*r,

gdzie:
r – promień okręgu wpisanego w romb
a – Długość boku rombu

Więcej na temat rombu i jego własności dowiesz się, rozwiązując nasze kursy maturalne. Poznasz również wzory na trapez, równoległobok i inne figury geometryczne.