Trapez

Zanim przejdziesz do ćwiczeń powtórzeniowych, warto utrwalić podstawowe informacje z geometrii, takie jak własności trapezu, wzory i rodzaje tego czworokąta. Przygotowaliśmy krótką pigułkę, która pomoże Ci utrwalić wiedzę z poprzednich lat. Możesz również ją wydrukować i trzymać na biurku jako pomoc przy rozwiązywaniu równań w trakcie powtórek.

Definicja: Trapez jest wypukłym czworokątem, który ma przynajmniej jedna parę boków równoległych. Są to jego podstawy. Pozostałe boki to ramiona trapezu. Wysokość trapezu to odległość pomiędzy jego podstawami.

Rodzaje trapezów: Szczególnym rodzajem trapezu są trapez prostokątny oraz trapez równoramienny. Trapez prostokątny ma przynajmniej jedno ramię prostopadłe do podstaw. Ramie prostopadłe do podstawy jest jednocześnie wysokością trapezu. Kwadrat i prostokąt są szczególnymi przypadkami trapezu prostokątnego.

>> Chcesz dobrze zdać maturę z matematyki? Zobacz ebook Matematyka część 3.

Ramiona trapezu równoramiennego mają równe długości. Przekątne trapezu równoramiennego mają jednakową długość. Suma miar przeciwległych kątów w trapezie równoramiennym wynosi 180°.

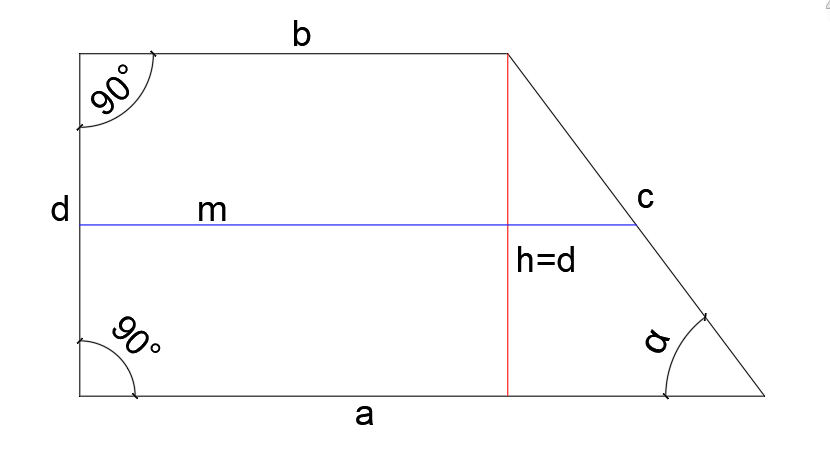
Własności trapezu

– trapez ma przynajmniej jedną parę boków równoległych;

– linia środkowa trapezu (m), to odcinek łączący środki jego ramion.

Wzory na wymiary trapezu

1. Wzór na pole trapezu:

Pole trapezu oblicza się korzystając ze wzoru:

$P=\frac{(a+b)\cdot h}{2}$ , gdzie

Długość jednej podstawy trapezu,
Długość drugiej podstawy trapezu

h- wysokość trapezu

2. Środkowa linia trapezu, to odcinek łączący środki ramion trapezu. Liczona jest ze wzoru

$m=\frac{a+b}{2}$

Powyższy wzór może posłużyć zatem również obliczeniu pola powierzchni trapezu. Pole powierzchni trapezu można zatem policzyć ze wzoru:

P=m*h

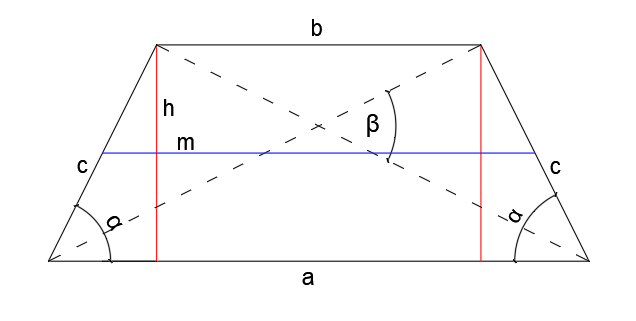
3. Pole trapezu równoramiennego można również obliczyć ze wzoru:

$P=\frac{1}{2}e^2\cdot sin\beta$ ,

gdzie:
e- przekątna trapezu równoramiennego,
β- kąt między przekątnymi trapezu równoramiennego.

4. Obwód trapezu

Obwód trapezu liczony jest ze wzoru:

L=a + b + c + d,

gdzie:
a, b – długość podstaw trapezu,
c, d – długość ramion trapezu,

Obwód trapezu równoramiennego można obliczyć ze wzoru

L=a+b+2c,

gdzie:
a, b – długość podstaw trapezu,
c– długość jednego z ramion trapezu.

Żeby utrwalić wiedzę na temat właściwości trapezu i innych zagadnień z matematyki, polecamy nasze kursy maturalne. Poznasz również wzory na romb, równoległobok czy inne figury geometryczne.